Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering (NeurIPS'16)
Contents
Convolutional Neural Network on Graphs with Fast Localized Spectral Filtering (2016)은 NeuIPS에 나온 논문으로 처음으로 ChebNet을 제안한 논문이다. ChebNet은 Chebyshev polynomial을 사용한 네트워크이며, 논문을 읽으면서 자세하게 다루어보자. 본 글은 요약을 하는 것이 목적이기 때문에 관련 연구 항목은 리뷰를 하지 않을 것이다(관련 연구는 개인적으로).
Abstract
CNN의 구조는 일반적으로 음성, 비디오, 이미지 등의 분야에 많이 사용되었다.그러나, 소셜 네트워크, 뇌 구조, 그래프 표현 등의 고차원적인 구조를 다루는 것에 있어서는 어려움이 존재하기 때문에 본 연구는 CNN(Convolution Neural Network)를 일반화하는 것에 관심을 두고 있다. Spectral Graph Theory를 기반으로 한 CNN의 formulation를 제시한다. Spectral Graph Theory는 Graph에서 Convolution Filter를 설계하는 것에 필요한 수학적인 배경과 효율적인 계산을 제공한다. 중요한 것은, 본 논문에서 제안하는 기법이 기존의 CNN과 동일한 선형 계산복잡도와 일정한 학습 복잡도를 제공한다는 것이다. MNIST와 20NEWS 데이터를 사용하여 실험을 진행하여 본 논문에서 제안하는 딥러닝 모델이 local, stationary, compositional feature을 학습하는 능력을 증명하였다.
간단하면서 효율적인 Spatial Convolution Network를 사용하지 않고 Spectral Convolution Network를 사용하는 근본적인 이유가 바로 수학적인 배경과 효율적인 계산 방식을 제공한다는 것이다. 기존의 Spectral CNN 연구에서는 모든 노드에 대해서만 고려하여 연구를 진행하였다. 따라서, 그래프의 구조가 복잡하고, 노드의 수가 많아지면 많아질수록 계산 비용이 엄청나게 비싸진다. 반면에, 본 논문에서 제안하는 ChebNet의 경우 기존의 CNN과 동일한 선형 계산복잡도와 일정한 학습 복잡도를 제공한다는 것이 핵심이다.
Introduction
CNN은 큰 스케일과 고차원의 데이터셋에서 매우 의미있는 통계적인 패턴을 추출하기 위한 효율적인 구조를 제공한다. AlexNet을 기점으로 이미지 뿐만 아니라 비디오, 음성 등 다양한 분야에서 CNN을 접목시키고자 하는 연구가 진행되고 있다. CNN은 Convolution Filter를 통해 파라미터를 공유함으로써 Local feature를 추출하며, 이는 물체가 움직이거나 조금 변형되더라도 동일한 기능을 발휘한다. 다시 말해, 이미지 내에 강아지가 왼쪽에 있는 이미지를 학습하고, 검증용으로 강아지가 오른쪽에 있는 이미지에 대해서도 강아지라고 분류할 수 있다는 것을 의미한다.
소셜 네트워크에서의 사용자, 바이오에서 유전자 등의 데이터는 이미지와 같이 Euclidean 구조를 가지고 있는 것이 아니라 non-Euclidean 구조를 가지고 있다. 이와 같은 구조는 heterogeneous Graph로 구성할 수 있다. Graph는 이와 같이 복잡한 기하학적 구조를 encode할 수 있으며, Spectral Graph Theory와 같은 수학적 tool로 연구할 수 있다.
CNN은 Euclidean 구조에서 convolution 연산과 pooling 연산이 가능하기 때문에, 이를 Graph Filter로 사용하기에는 이론적으로나 구현하는 것으로나 어려운 실정이다. 본 연구에서는 효율적으로 Graph Filter를 정의하고 학습하는 것을 목적으로 설정하였으며, 다음과 같은 기여를 했다.
1. Spectral formulation.
Graph Signal Processing (GSP)에서 이미 검증된 tool을 기반으로 구축된 그래프에 대한 CNN를 이론적으로 공식화하였다.
2. Strictly localized filters.
기존 연구에서 제안된 Spectral filter보다 성능이 향상되었다. 본 논문에서 제안한 Spectral filter는 K-hop을 엄격하게 제안함으로써 학습 과정에서의 불안정성을 해결하여 성능을 개선하였다.
3. Low computational complexity.
본 연구에서 제안하는 filter는 선형 K개의 filter와 edge에 대해 선형적인 계산 복잡도를 가진다. 실제 필드에서 사용하는 그래프는 매우 sparse한 구조를 가지고 있다. 제안한 Graph filter는 k개의 이웃만을 고려하기 때문에 $|\mathcal{E}| < n^2$ and $|\mathcal{E}| = kn$만큼의 시간 복잡도를 가진다. 게다가, 이 방법은 푸리에 변환을 기반으로 하지 않기 때문에(orthogonal based가 아니라 Polynomial based), 이를 계산하기 위한 EigenValue Decomposition (EVD)와 $n^2$ 크기의 행렬인 basis를 저장할 필요가 있다. 이와 같은 개념은 제한된 GPU를 사용할 때, 기존 연구와는 달리 GPU에서 Eigenvalue를 구하기 위한 연산이 진행되지 않기 때문이다. 추가적으로 $|\mathcal{E}|$의 희소행렬인 Laplacian만 저장하면 된다.
4. Efficient pooling.
노드를 이진 트리 구조로 재배열하고, 1D signal 풀링과 유사한 효율적인 풀링 전략을 제안한다.
5. Experimental results.
본 논문에서 제안한 모델이 MNIST 데이터에서 기존의 CNN과 유사하게 수행되는 것을 보여주고, 다양한 그래프의 구성이 성능에 미치는 영향에 대해 연구하였다.

Proposed Technique
CNN를 그래프로 일반화하기 위해서는 3 가지의 기본적인 단계가 필요하다. 첫 번째로는, 그래프에서 지역화된 Convolutional filter를 설계하는 것이다. 두 번째로는, 유사한 이웃을 그룹화하는 coarsening procedure를 적용한다. 마지막으로는, 그래프 풀링 연산을 수행한다.
Learning Fast Localized Spectral Filters
Convolution filter는 spectral filter와 spatial filter로 나눌 수 있다. 본 논문에서는 Convolution Theorem을 기반으로 한 spectral filter를 사용한다. Convolution Theorem은 푸리에 변환을 기반으로 학습하는데, 이와 같은 연산은 $\mathcal{O}(n^2)$의 계산 복잡도를 보인다.
Graph Fourier Transform
본 논문은 푸리에 변환의 문제점을 지적하면서 ChebNet 을 제안하였다. 그렇다면 일단 먼저 푸리에 변환이 어떤 것인지부터 알아보자. 본 논문에서는 undirected and connected graph $\mathcal{G} = (\mathcal{V, E}, W)$에 정의된 신호 처리를 다룬다. $\mathcal{V}$는 노드의 집합을 의미하고, $\mathcal{E}$는 엣지의 집합을 의미한다. 그리고, $W \in \mathbb{R}^{n \times n}$은 인접 행렬(Adjacency matrix)을 의미한다. signal $x : \mathcal{V} \rightarrow \mathbb{R}$은 그래프 노드에 정의된 vector $x \in \mathbb{R}^n$로 간주될 수 있다. 예를 들면, 소셜 네트워크에서 사용자의 나이, 연령 등의 정보를 담고 있는 vector를 의미한다.
Spectral Graph analysis에서 필수적인 연산은 바로 Graph Laplacian이다. Laplacian Matrix는 $L = D - W$로 차수 행렬($D \in \mathbb{R}^{n \times n}$)과 인접행렬로 구성된다. Laplacian Matrix를 Laplacian normalization을 수행하게 되면 $L= I_n - D^{-\frac{1}{2}} W D^{-\frac{1}{2}} $로 표현할 수 있으며, $I_n$는 항등 행렬(identity matrix)을 의미한다. Laplacian Matrix는 대칭 반정부호(Positive semidefinite) 행렬이기 때문에 정규 직교 집합 ${u_l}^{n-1}_{l=0} \in \mathbb{R}^n$를 가진다.
푸리에 변환은 그래프를 고유분해하는 것이므로 다음과 같은 수식으로 표현할 수 있다.
\[ L = U\Lambda U^T \]
$U=[u_0, ..., u_{n-1}] \in \mathbb{R}^{n \times n}$를 의미한다. 즉, 직교 행렬을 나타낸다. $\Lambda= \text{diag}([\lambda_0, ..., \lambda_{n-1}]) \in \mathbb{R}^{n \times n}$를 의미한다. signal $x \in \mathbb{R}^n$의 푸리에 변환은 $\hat{x} = U^Tx \in \mathbb{R}^n$으로 정의할 수 있다. $U$는 직교행렬이기 때문에 $U^{-1} = U^T$가 성립한다. 따라서, $x = U \hat{x}$로 표현할 수 있다.
Spectral filtering of graph signals
본 논문에서는 Convolution Theorem을 통해서 Convolution 연산을 그래프에 적용하고자 했다. Convolution Theorem과 푸리에 변환을 사용하여 다음과 같은 수식을 도출하였다.
\[ \begin{equation} \begin{split} \mathcal{F}(f \star g) & = \mathcal{F}\{f\} \odot \mathcal{F}\{g\} \\ x *_{\mathcal{G}} y & = \mathcal{F}^{-1} ( \mathcal{F}(x) \odot \mathcal{F}(y)) \\ x *_{\mathcal{G}} y & = U((U^T x) \odot (U^T y)) \\ \end{split} \end{equation} \]
이때 x는 node에 대한 정보를 의미하고, y는 Graph Convolution Filter를 의미하며, y는 다음과 같이 정의할 수 있다.
\[ \begin{equation} \begin{split} y & = g_{\theta} (L)x = g_{\theta} (U \Lambda U^T ) x = U g_{\theta} (\Lambda) U^T x \end{split} \end{equation} \]
그러나 기존의 CNN과는 다르게 이때의 $g_{\theta}(\Lambda) = \text{diag}(\theta) $는 non-parametric filter이다. 기본적으로 푸리에 변환이 그래프를 고유 분해함으로써 도출되는 고유값과 고유벡터를 사용하기 때문에 이는 학습이 불가능하기 때문이다. 이처럼 non-parametric filter는 두 가지의 문제점이 존재한다. 첫 번째, 공간에 국한되지 않는다. 기존의 GCN 방식은 전체 그래프를 푸리에 변환을 통하여 고유값을 도출하고 이를 바탕으로 학습을 진행하였다. 그렇기 때문에 local한 정보를 반영하는 것이 어렵다. 두 번째, $\mathcal{O}(n)$의 시간 복잡도를 가지고 있어 데이터의 차원이 커지면 커질수록 계산의 양이 많아진다. 이러한 문제를 Polynomial Filter로 극복이 가능하다.
\[ \text{Polynomial Filter} = g_{\theta}(\Lambda) = \sum^{K-1}_{k=0} \theta_k \Lambda^k \]
이때 $\theta \in \mathbb{R}^K$는 polynomial의 계수를 의미한다. 이때 K 차수까지 고려하게 된다면, $K^{\text{th}}$-order polynomial이 되며, 시간 복잡도는 $\mathcal{O}(K)$가 된다.
Recursive formulation for fast filtering
기존의 푸리에 변환을 통한 연산의 전체 시간 복잡도는 $\mathcal{O}(n^2)$이다. 반면에, 본 논문에서 제안하는 polynomial filter를 사용하게 되면, $\mathcal{O}(K|\mathcal{E}|) << \mathcal{O}(n^2)$으로 시간 복잡도가 감소된다. 이때의 polynomial funtion은 Chebyshev polynomial funtion $T_k(x)$를 사용하며, 수식은 다음과 같다.
\[ T_k(x) = 2xT_{k-1} (x) - T_{k-2} (x), \ \text{with} \ T_0=1, \ \ T_1 = x \]
위 수식을 [-1, 1] 사이로 정규화하면 다음과 같은 수식이 도출된다.
\[ g_{\theta} = (\Lambda) = \sum^{K-1}_{k=0} \theta_k T_k(\tilde{\Lambda }) \]
이때 $\tilde{\Lambda} = 2\Lambda/\lambda_{\text{max}} - I_n $을 의미하며, 정규화할 경우 eigenvalue는 [-1,1] 사이의 값을 가진다. 이때 filtering operation 다음과 같이 표현할 수 있다.
\[ y = g_{\theta}(L)x = \sum^{K-1}_{k=0} \theta_k T_k (\tilde{L})x \]
위 수식은 기존의 수식을 Chebyshev polynomial로 변형한 것이다. 또한, 위 수식을 재귀 식으로 표현하면 $\bar{x}_k = 2 \tilde{L} \bar{x}_{k-1} - \bar{x}_{k-2}, \ \text{with} \ \bar{x}_0 = x \ \text{and} \ \bar{x}_1 = \tilde{L}x$로 표현할 수 있다. 최종 수식은 $y = g_{\theta}(L)x = [ \bar{x}_0, ..., \bar{x}_{K-1} ] \theta $가 되고, 시간 복잡도는 $\mathcal{O}(K|\mathcal{E}|)$가 된다.
Learning filters
sample $s$의 $j^{\text{th}}$ feature map은 다음과 같다.
\[ y_{s, j} = \sum^{F_{in}}_{i=1} g_{\theta_{i,j}} (L) x_{s, i} \in \mathbb{R}^n \]
이때 input feature map $x_{s,i}$와 Chebyshev coefficients $\theta_{i,j} \in \mathbb{R}^K$는 학습 가능한 parameter를 의미한다. 따라서, 역전파 알고리즘을 수행할 때 아래의 두 가지 Gradient가 요구된다.
\[ \begin{equation} \begin{split} \frac{\partial E }{\partial \theta_{i, j}} & = \sum^S_{s=1} [ \bar{x}_{s, i, 0}, ..., \bar{x}_{s, i, K-1} ]^T \cdot \frac{\partial E}{\partial y_{s,j} } \\ \frac{\partial E}{\partial x_{s,i}} & = \sum^{F_{\text{out}}}_{j=1} g_{\theta_{i,j}} (L) \cdot \frac{\partial E}{\partial y_{s,j}} \end{split} \end{equation} \]
$E$는 sample $S$의 mini-batch loss를 의미한다.
Graph Coarsening
본 논문에서는 coarser graph를 생성하는 multi-level clustering 중에서 Graclus Algorithm을 사용한다. 이를 통해 Sub-sampling을 하고 Pooling 작업을 수행하기 위함이다. Graclus Algorithm은 Greedy algorithm을 사용하여 입력으로 들어온 그래프를 Coarser version으로 계산하는 방식이다.
Fast Pooling of Graph Signals
위에서 사용한 Pooling 방식은 여러 번 수행되어야 한다. 한 번 수행한다고 하더라도 제대로 간소화되지 않기 때문이다. 또한, Coarser Graph는 정렬이 제대로 되지 않기 때문에 Pooling 작업을 직접 적용하려면 일치하는 모든 node의 정보를 저장할 테이블이 요구된다.
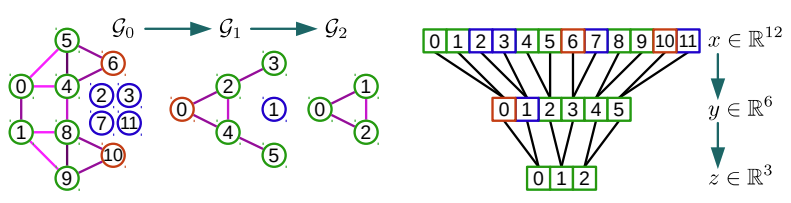
이 과정은 balanced binary tree를 생성하고 node를 재정렬하는 방식으로 총 두 단계로 구성되어 있다. 첫 번째로 왼쪽 그림처럼 tree 구조를 생성한 후에 오른쪽 그림처럼 정렬을 한다. 그 후 다시 coarser 과정을 수행하고, 이를 반복한다. 최종적으로는 [0, 1, 2]로 구성된 $z \in \mathbb{R}^3$이 도출된다.
Numerical Experiments
본 논문에서는 MNIST 데이터를 사용하여 성능을 검증하였다. MNIST는 28 X 28 사이즈를 가진 2D Grid 이미지 70,000 장으로 구성되어 있다. 실험을 위해 784 개의 pixel을 의미하는 node와 192개의 fake node로 구성된 8-NN graph 를 구성하였다.
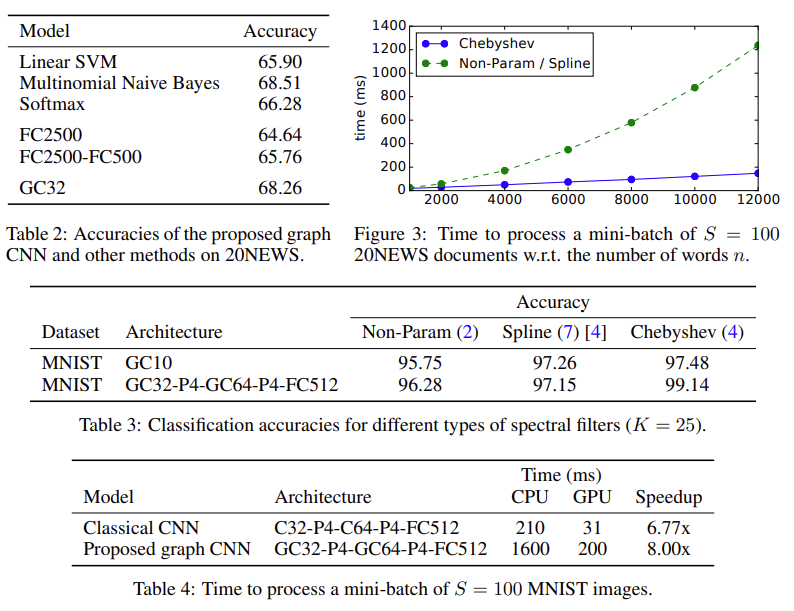
$FC_k$는 Fully Connected Layer를 의미하고, $P_k$는 Stride가 k인 Pooling Layer를 의미한다. $GC_k$와 $C_k$는 Convolution Layer를 의미하고, $S$는 배치 사이즈를 의미한다. 실험 결과, 본 논문에서 제안하는 ChevNet의 성능이 기존의 모델과 거의 동일한 성능을 발휘하는 것을 확인할 수 있다. 이 뿐만 아니라 기존에 비해 빠른 속도를 보여주고 있으며, NEWS20에서도 유사한 결과를 보여주고 있다.
Conclusion and Future Work
본 논문에서는 Graph Signal Processing (GSP)를 사용하여 CNN을 그래프 도메인에 효율적으로 일반화하는 개념을 소개하였다. 실험은 매우 효율적인 연산을 보여주고 있으며, 더 나은 결과를 도출하기도 했다. 이후, GSP에서 새로 개발된 tool을 사용하여 본 논문에서 제안하는 모델의 성능을 향상시키고자 하며, 데이터의 구조가 2D grid가 아닌 기본적으로 그래프 구조로 이루어져 있는 경우에 대해서도 실험을 진행하고자 한다.