Contents
백준이나 코드업 등 코딩 테스트에서 진행하는 알고리즘들에서 빅오(Big-O)라는 단어는 많이들 들어봤을 것이다. 그렇다면 빅오메가, 빅세타는 무엇일까? 먼저 빅오부터 알아보자.
빅-오(Big-O)
빅오는 코딩 테스트에서 시간복잡도를 다룰 때 주로 사용된다. 대개 최악의 경우를 의미하며, $\text{O(n)}, \text{O(n log(n)} $ 등 다양하게 존재한다. 예를 들어, 입력값 $n$에 대해서 $4n^2 + 3n + 4$ 번 만큼 계산하는 함수가 있다면, 최고차항만 고려하고 계수는 무시한다. 즉, 이때의 시간 복잡도는 $\text{O}(n^2)$이 되는 것이다. $\text{O}(1)$대부분 $\text{O}(\text{n})$을 기준으로 빠름을 나눈다.
\[ \text{O}(1) \]
\[ \text{O}(\log \text{n}) \]
\[ \text{O}(\text{n}) \]
\[ \text{O}(\text{n} \log \text{n}) \]
\[ \text{O}(\text{n}^2) \]
\[ \text{O}(2^{\text{n}}) \]
\[ \text{O}(\text{n!}) \]
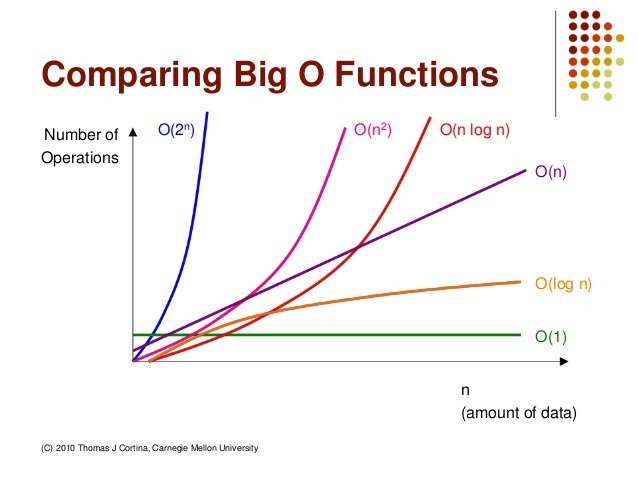
$\text{O}(1)$는 입력값이 아무리 커도 실행 시간은 일정하다. $\text{O}(\log n)$의 실행 시간은 입력값에 영향을 받는다. $\text{O}(n)$은 입력값만큼 실행 시간에 영향을 받으며, 알고리즘을 수행하는 데 걸리는 시간은 입력값에 비례하고, 이러한 알고리즘을 선형 시간 알고리즘이라고 한다. 정렬되지 않은 리스트에서 최댓값 혹은 최솟값을 찾는 경우가 이에 해당된다. $\text{O}(n \log n)$은 대부분의 효율 좋은 정렬 알고리즘이 이에 해당한다. 적어도 모든 수에 대해 한 번 이상은 비교해야 하는 비교 기반 정렬 알고리즘은 아무리 좋은 알고리즘도 $\text{O}(n \log n)$보다 빠를 수 없다. $\text{O}(n^2)$은 비효율적인 정렬 알고리즘일 때 해당 시간 복잡도를 가진다. $\text{O}(2^n)$은 피보나치 수를 재귀로 계산하는 알고리즘의 시간 복잡도를 의미한다. 마지막으로 $\text{O}(n!)$은 가장 느린 알고리즘으로 입력값이 조금만 커져도 웬만한 다항 시간 내에는 계산이 어렵다.
빅-오메가(Big-Omega)
빅오메가는 빅오와는 반대되는 개념이다. 빅오는 최대 얼마나 걸리는지를 다루었다면, 빅오메가는 최소 얼마만큼 걸렸는지를 다루는 용어이다. 빅오와 다른점은 부등호의 방향이 반대이기 때문에 위에서 언급한 것들의 효율적인 순서가 역순입니다.
\[ \Omega (\text{n!}) \]
\[ \Omega (2^{\text{n}}) \]
\[ \Omega (\text{n}^2) \]
\[ \Omega (\text{n} \log \text{n}) \]
\[ \Omega (\text{n}) \]
\[ \Omega (\log \text{n}) \]
\[ \Omega (1) \]
가장 이상적인 알고리즘은 빅오와 빅오메가 둘다 낮은 알고리즘이지만 실제 대부분의 알고리즘은 빅오와 빅오메가가 반비례하는 관계를 가지고 있기에 둘 다 낮은 알고리즘은 존재하지 않는다고 한다. 둘 중 하나를 선택하라고 한다면 빅오가 낮은 알고리즘이 조금 더 낫다고 한다.
빅-쎄타(Big-Theta)
빅세타는 빅와 빅오메가의 가운데라고 할 수 있다. 평균적인 복잡도를 의미하나 일반적으로는 잘 사용하지 않는다고 한다. 평균적인 복잡도보다는 최선 혹은 최악의 상황에서 알고리즘을 많이 사용하기 때문이다.
'Python > Algorithm' 카테고리의 다른 글
| [프로그래머스] 달리기 경주 - Python (0) | 2023.08.24 |
|---|---|
| [Algorithm] sort()와 sorted()의 차이점 (2) | 2022.08.18 |
| [Algorithm] List, Dictionary의 시간 복잡도 (0) | 2022.08.18 |
| [Python] python에서 pickle file 다루기 (0) | 2022.06.20 |
| array와 asarray의 차이 (0) | 2022.05.09 |