Contents
그래프를 통한 influence는 정보 혹은 행동, 고장, 질병 등 다양한 influence가 존재할 수 있다. 예를 들어, 온라인 소셜 네트워크를 통해 다양한 정보를 전파할 수 있다. 컴퓨터 네트워크에서는 일부 장비의 고장이 전파되어 전체 네트워크를 마비시킬 수도 있다. 최근에 이슈가 된 코로나-19라는 질병이 사회라는 거대한 소셜 네트워크를 통해 전파되는 것도 언급할 수 있다. 이처럼 다양한 influence를 그래프로 표현할 수 있을 것이다.
이와 같은 전파 과정을 체계적으로 이해하고 대처하기 위해서는 그래프의 구조를 제대로 이해하고 있어야 한다. 본 글에서는 Cascade model 중 두 가지 모형을 다룬다. 첫 번째 모형은, 의사결정 기반의 Cascade model이다. 먼저 의사결정 기반의 Cascade model을 알아보자.
Cascade model based on decision-masking
사용자는 제품을 구매할 때 주변 사람들의 의사결정을 참고하여 본인의 의사결정을 진행하는 경우가 존재한다. 예를 들어, 카카오가 라인이 있을 때 만약 일본에 거주하는 사용자라면 주변에 라인을 쓰는 사용자가 많아서 주로 라인을 쓸 것이다. 반면에, 한국에 거주하는 경우 대부분의 사용자들이 카카오톡을 사용하기 때문에 카카오톡을 사용하는 것이 보다 편할 것이다.
본 글에서는 의사결정 기반의 Cascade model은 Linear Threshold Model(LTM)을 다루어볼 것이다. LTM은 이름에서도 유추해볼 수 있듯 전파량의 Threshold를 기점으로 선형 분류하는 모델이다.
예를 들어, user $u$와 user $v$가 있다고 가정하자. 두 사용자는 카카오, 라인 중 하나를 메세지 플랫폼으로 선택하여야 한다. 둘 모두 카카오톡을 사용하는 경우 호환이 잘되어 $a$ 만큼 행복이 증가하며, 둘 모두 라인을 사용하는 경우 호환이 잘되어 $b$만큼 행복이 증가한다. 반면에, 두 사용자의 메세지 플랫폼이 다른 경우 연락이 불가능해 증가하는 행복의 양이 0이 된다.

이때 빨간색은 카카오톡, 파란색은 라인을 의미한다. 위 예시를 확장해 소셜 네트워크를 고려해보자. 소셜 네트워크에서는 여러 사람과 연결 관계를 지닐 수 있다. 따라서, 소셜 네트워크 상으 이웃 사이에 발생하는 값을 고려하여야 한다. user $u$가 카카오톡을 선택할 경우 2$a$만큼 증가하지만, 라인을 선택할 경우 3$b$만큼 값이 증가한다. 이를 고려해 행복이 최대가 되는 방향으로 선택하여야 한다.
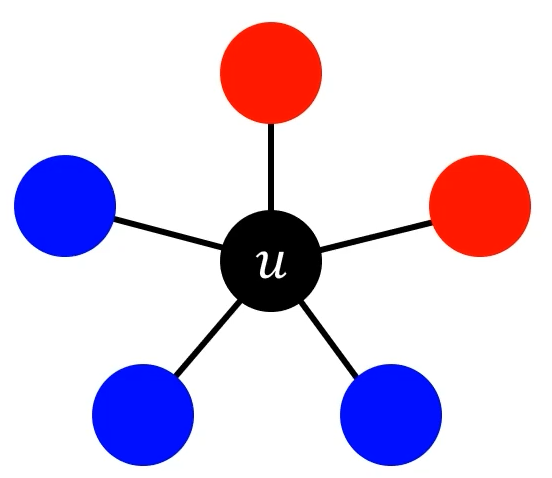
2$a$ > 3$b$라면 카카오톡을 선택할 것이고, 2$a$ < 3$b$라면 라인을 선택할 것이다. 위 예시에서 카카오톡을 A로 설정하고 라인을 B로 설정한 후 이를 일반화하면 다음과 같다. p 비율의 이웃이 A를 선택했다고 가정하고, (1-p) 비율의 이웃이 B를 선택했다고 가정하자. 그럼 이때 user $u$가 언제 A를 선택해야 할까? $ap > b(1-p)$가 될 때다. 이를 정리하면 $p > \frac{b}{a + b} $가 되며 $\frac{b}{a+b}$를 임계치 $q$라고 할 수 있다. 위 방식을 바로 Linear Threshold Model이라 한다.
Example


임계치 $q$를 55%로 가정하고 node $u$와 node $v$를 Seed Set이라고 가정하자. node $u$와 node $v$만 연결된 노드들은 임계치를 넘어서기 때문에 오른쪽 그림처럼 빨간색으로 mapping될 것이다.


위 과정을 계속 반복하면 오른쪽 그림에서 노드들이 더이상 변화하지 않고 값이 수렴하게 된다. Linear Threshold Model은 위 노드들이 더이상 변화하지 않을 때까지 혹은 iteration이 끝날 때까지 계속 반복하면서 업데이트를 진행한다.
Probability Cascade Model
코로나와 같은 경우 전파는 확률적으로 진행된다. 따라서, 확률적 전파 모형(Probability Cascade Model)을 고려하여야 한다. 본 글에서는 가장 간단한 확률적 전파 모형인 독립 전파 모형(Independent Cascade Model)을 다룬다. Independent Cascade Model을 알아보기 위해 방향성이 있고, 가중치가 있는 그래프를 가정해보자.
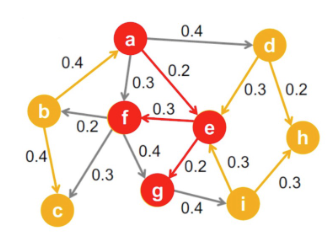
edge $(u,v)$의 가중치 $p_{uv}$는 $u$가 감염되고, $v$가 감염되지 않았을 때 $u$가 $v$를 감염시킬 확률을 의미한다. 즉, 각 node $u$가 감염될 때마다, 각 이웃 $v$는 $p_{uv}$확률로 전염된다는 것을 의미한다. 빨간색 노드를 감염자, 노란색 노드를 비감염자라고 한다면, $g$가 코로나에 감염되고 $i$에게 전파할 확률은 0.4가 되는 것이다. 여기에서도 마찬가지로 첫 번째 감염자를 Seed Set이라고 부른다. 최초 감염자들로부터 시작되며, 각 확률에 따라 코로나를 전파하고, 더이상 새로운 감염자가 없을 시 종료한다. 이때 Independent Cascade Model은 감염자는 계속 감염자 상태로 남아있는 것을 가정하고 있으나, 감염자의 회복을 가정하는 SIS, SIR 등의 다른 전파 모형도 존재한다.
'Deep Learning > Graph Neural Network' 카테고리의 다른 글
| Node Embedding (0) | 2022.09.02 |
|---|---|
| Community Detection (0) | 2022.09.02 |
| Link Prediction with DGL (0) | 2022.09.01 |
| DGL을 통한 Graph 생성하기. (0) | 2022.09.01 |
| Graph Convolution Network 구현 wtih DGL (0) | 2022.09.01 |