[Bayesian] Bayesian Deep Learning - Probability

본 자료는 edwith 최성준님이 강의하신 Bayesian Deep Learning 강의를 참고하였다.

 

핵심 키워드

$Probability$, $Samplespace$, $Randomexperiment$, $Probabilitymassfunction$, $Baye{s}^{\prime }Theorem$, $Expectation$

 

 

Probability

---

공정한 주사위 게임을 예로 들어보자. $\sigma$-field 는 power set이 될 것이고, subset은 $A$가 될 것이다. 여기서 주사위가 1이 나올 확률은 얼마인지 정의할 수 있어야 하고, 1이 나오거나 6이 나올 확률, 주사위가 1~5 사이에 하나가 나올 확률이 얼마인가에 대해서 정의할 수 있어야한다. 모든 가능한 조합을 표현할 수 있어야 하기 때문이다. 

이제부터 $\mathrm{\Omega }$ 를 B라고 부를 것이다. 

 

fair dice 

$LetP(\{1\})=P(\{2\})=P(\{3\})=P(\{4\})=P(\{5\})=P(\{6\})=\frac{1}{6}$

$P(A)=P(2,4,6)=P(\{2\})+P(\{4\})+P(\{6\})=\frac{1}{2}$ 

 

여기서 우리는 measure를 probability 로 아직 받아들이면 안된다. probability는 sample space에서 정의된 면적이다 라고만 받아들여야 한다. 

 

 

• The ramdon experiment should be well defined.
• outcomes : 나올 수 있는 모든 관측된 sample space에서 어떤 것이 정해진 후 나오는 값
• sample point $w$ : a point representing an outcome. $w\in \mathrm{\Omega }$ {1, 2, 3, 4, 5, 6}
• sample space $\mathrm{\Omega }$ : the set of all the sample points.  

 

 

 

Definition ( probability )

$P$ defined on a measurable space $(\mathrm{\Omega },A)$ is a set function

$P:A\to [0,1]$ such that (probability axioms).

     1. $P(\mathrm{\varnothing })$ = 0 

     2. $P(A)\le 0,\mathrm{\forall }A\subseteq \mathrm{\Omega }$

     3. For disjoint sets $A_i$ and $A_j\Rightarrow P({\cup }_{i=1}^k{A}_i)={\mathrm{\Sigma }}_{i=1}^{k}P(A)$ (countable additivity)

     4. $P(\mathrm{\Omega })$ = 1

 

 

그렇다면 위 axioms을 만족하는 probability 를 어떻게 만들 수 있을까? 

 

Probability allocation function

$\cdot$For discrete $\mathrm{\Omega }$ :

    $p:\mathrm{\Omega }\to [0,1]$ such that ${\mathrm{\Sigma }}_{w\in \mathrm{\Omega }}p(w)$ = 1 and $P(A)={\mathrm{\Sigma }}_{w\in A}p(w)$

$\cdot$For continuous $\mathrm{\Omega }$:

    $f:\mathrm{\Omega }\to [0,\mathrm{\infty })$ such that ${\int }_{w\in \mathrm{\Omega }}f(w)dw$ = 1 and $P(A)={\int }_{w\in A}f(w)dw$

Recall that probability $P$ is a set function $P:A\to [0,1]$ where $A$ is a $\sigma$-field

 

아래에 보이는 검은색 선은 sample space에 들어가 있고, 그때의 면적을 측정하면 probability가 된다.

example

 

conditional probability of A given B

$P(A|B)\triangleq \frac{P(A\cap B)}{P(B)}$

$P:A\to [0,1].$

conditional probability

 

Chain rule

     - $P(A\cap B)=P(A|B)P(B)$

     - $P(A\cap B\cap C)=P(A|B\cap C)P(B\cap C)=P(A|B\cap C)P(B|C)P(C)$ 

 

total probability law:

$P(A)=P(A\cap B)+P(A\cap B^c)$

$=P(A|B)P(B)+P(A|B^c)P(B^c)$

 

Bayes' rule

$P(B|A)=\frac{P(B\cap A)}{P(A)}=\frac{P(A\cap B)}{P(A)}=\frac{P(A|B)P(B)}{P(A)}$

 

 

When $B$ is the event that is considered and $A$ is an observation

• $P(B|A)$ is called posterior probability
• $P(B)$ is called prior probability

prior probability가 주어지고 posterior probability를 찾는 것이 bayesian이라고 할 수 있다.

 

 

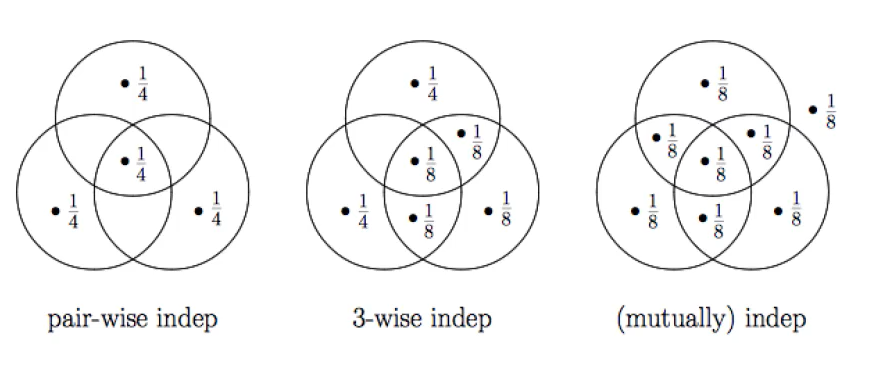
independent events $A$ and $B$ : $P(A\cap B)=P(A)\ast P(B)$

independet event를 번역 그대로 관계없는 독립적인 사건이라고 보는 것이 아니라, $A$와 $B$의 교집합과 $A$와 $B$의 확률을 각각 곱한 값이 같은 것을 independent events 라고 부른다. A,B가 멀리 떨어져있으면 indenpendent하지 않다.

 

independent $\ne$ disjoint, mutually exclusive

 

 

independent