Restricted Boltzmann Machines(RBM)은 제한된 볼츠만 머신이라는 뜻이다. RBM은 Generative Model이라고도 부른다. 일반적으로 DNN, CNN, LSTM 등과 같은 Deterministic Model 과는 다른 방식의 접근 방법이다. 우리가 일반적으로 사용하는 Deterministic Model은 loss function을 '지표'로 활용해 오차를 줄이는 것을 목표로 하지만,Generative Model의 경우 확률밀도함수(probability density function; pdf)를 모델링하는 것을 목표로 삼는다.
이미지를 예로 들면 이미지를 생성할 때 눈, 코, 입 등의 다양한 부분을 생성한다고 가정하자. 그렇다면 눈의 모양은 동그라미일수록 확률값이 높을 것이다. 만약 눈의 모양이 별표라면 가장 낮은 확률값을 가질 것이다. 이렇게 여러 사건들의 확률이 가장 높은 방향으로 접근해 생성하는 것이다. 이와 같은 모델이 GAN이 있다. Generative Model은 Explicit model과 implicit model로 나뉘는데, 앞에서 언급한 GAN의 경우 단순히 이미지 생성에만 관여하는 모델을 implicit model이라고 지칭하며, 어떤 이미지가 들어왔을 때 기존의 이미지와 얼마나 유사한가 확률값을 출력해내는 annomaly detection과 같은 행위를 하는 모델은 Emplicit model이라고 부른다.
마르코프 모델(Markov Model)
Generative model인 RBM을 설명하기에 앞서 먼저 알아야할 모델들이 존재한다. 첫 번째로는 마르코프 모델(Markov Model)이다. 마르코프 모델은 시점 T에 어떤 상태(state)로 들어갈 확률은 시점 T-1의 상태에만 의존한다는 것이다. 예를 들자면, 어제의 일이 오늘에만 영향을 미친다는 것이다. 마르코프 모델은 $\boldsymbol{V} = \{v_1, ..., v_m\}$과 같이 m개의 상태를 각각 정의한다. 그 후 각각의 상태 간 일어날 확률을 의미하는 상태 전이 확률을 정의할 수 있다. 상태 전이 확률 $a_{ij}$는 상태 $v_i$에서 상태 $v_j$로 이동할 확률을 의미하며 수식으로 표현하면 다음과 같다.
\[ a_{ij} = P(o_t = v_j \ | \ o_{t-1} = v_i) \]
\[ a_{ij} > 0 \ and \ \sum_{j=1}^m a_{ij} = 1 \]

볼츠만 머신(Boltzmann Machine, BM)
두 번째로는 마르코프 모델의 일종인 볼츠만 머신(Boltzmann Machine)이다. BM은 확률분포(위에서 언급한 pdf)를 학습하기 위해 만들어졌다고 할 수 있다. BM의 가정은 "우리가 보고 있는 것들 외 보이지 않는 요소들까지 잘 포함시켜 학습할 수 있다면, 확률 분포를 보다 정확하게 알 수 있지 않을까?"라는 것이다.
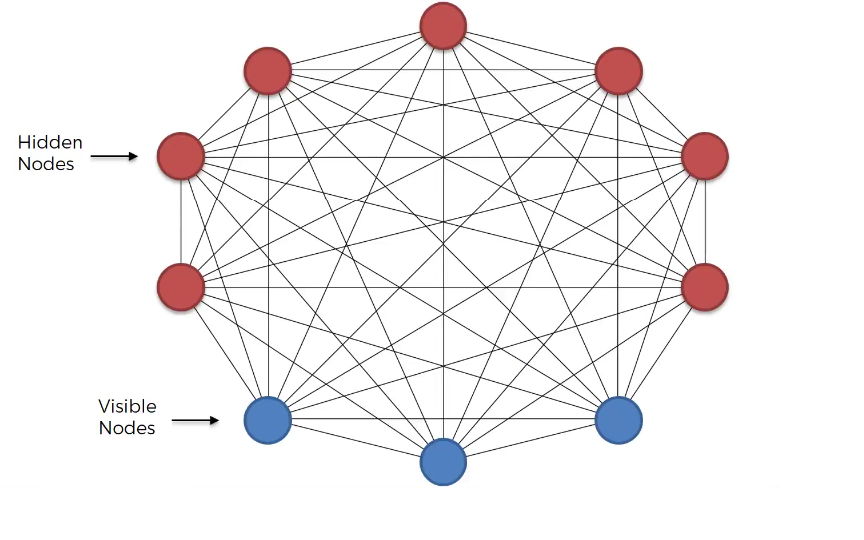
위 그림에서 보이는 것 처럼 BM은 hidden node(unit)과 visible node(unit)로 구성되어 있다. hidden node의 경우 우리가 보지 못하는 어떠한 특성의 존재를 의미하고, visible node는 우리가 볼 수 있는 특성을 의미한다. 각각의 에지(edge)는 서로의 연결성을 의미한다. 모델을 학습할 때 hidden node까지 학습할 수 있다면 보다 정확한 확률분포를 학습할 수 있다는 것을 전제로 한다. 볼츠만 머신은 d차원 이진 확률 벡터 $\boldsymbol{x} \in \{ 0, 1 \}^d$에 관해 정의된다. 볼츠만 머신의 결합 확률 분포는 다음과 같이 에너지 함수를 통해 정의할 수 있다.
\[ P(\boldsymbol{x}) = \frac{\exp(-E(\boldsymbol{x}))}{Z} \]
$E(\boldsymbol{x})$는 에너지 함수를 의미하고, $Z$는 $\sum_xP(x)=1$이 되도록 하는 정규화항이다. BM에서는 특이하게 loss function을 에너지 함수로 정의하였다. 에너지라는 개념은 물리학에서 차용한 것이라고 하며, 특정 상태(configuration) $x$에 대한 에너지를 $E(x)$라고 한다면, $E(x)$는 그 상태에 매칭되는 값을 의미한다. $E(\boldsymbol{x})$는 다음과 같이 정의할 수 있다.
$E(\boldsymbol{x}) = -x^T Ux - b^T x $
여기서 $U$는 매개 변수의 가중치 행렬을 의미하고, b는 bias를 의미한다. 위와 같은 형태로도 사용이 가능하지만, 간단하기 때문에 변수들 사이의 상호작용의 종류가 상당히 제한적이게 된다. BM은 모든 변수가 관측되지는 않을 때 즉, hidden node가 존재할 때 조금 더 성능이 좋다고 알려져있다. 딥러닝에 빗대어 살펴보면 딥러닝의 hidden layer가 BM의 hidden node와 같은 역할을 수행한다. BM에 이와 같은 hidden node(unit)을 추가하면 보다 좋은 성능을 보일 수 있으며, hidden node를 추가한 수식은 다음과 같다.
$E(v, h) = -v^TRv - v^TWh - h^TSh - b^Tv - c^Th $
$x$를 $v,h$로 구성되었다고 가정한다. $v, h$는 각각 visible unit과 hidden unit을 의미한다. BM을 학습할 때에는 MLE(Maximum Likelihood Estimate)를 사용한다.
제한된 볼츠만 머신(Restricted Boltzmann Machine, RBM)
우리는 RBM을 설명하기 위해 마르코프 모델과 BM에 대해서 언급했다. 그렇다면 RBM은 어떤 것일까? RBM은 심층 확률 모형을 구축하는 데 가장 흔이 사용되는 요소이며, 관측 가능한 변수들로 이루어진 층 하나와 잠재변수들로 이루어진 층 하나를 담은 무향 확률 그래프 모형이다. 여기서의 무향은 방향성이 없다라는 의미이다. BM의 경우에는 각 unit간 연결이 되어 있지만, RBM의 경우 visible unit과 hidden unit 사이에만 연결이 존재하고, 같은 Layer끼리는 아무런 연결성이 없는 이분 그래프(bipartite graph) 이다.
각 Layer 간 내부적 연결이 없어진 것은 사건 간 독립성을 가정함으로써 확률분포의 결합을 쉽게 표현하기 위해서이다. 또한 visible layer와 hidden layer 만을 연결함으로써 visible layer가 주어졌을 때 hidden layer의 데이터를 계산할 수 있도록 하거나, 그 역도 가능하도록 하는 조건부 확률을 계산하기 위함이다.
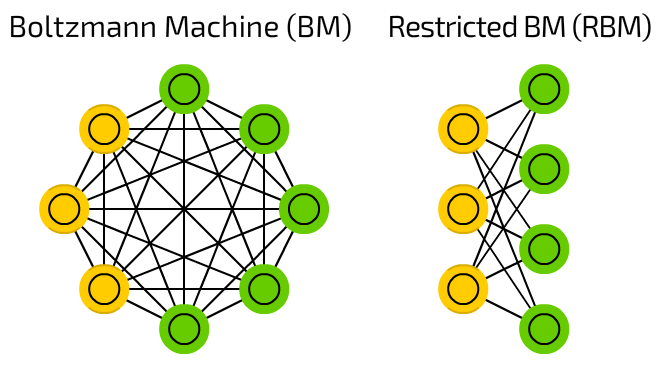
RBM의 구성을 살펴보면 딥러닝의 구조와 매우 흡사한 모형을 가지고 있다. 모형만 흡사한 것이 아니라 실제로 RBM은 Feed-Forward Neural Network(FFNN)처럼 학습을 한다. 여기서는 노란색 부분인 visible unit은 $\boldsymbol{v}$로 표기하고, 초록색 부분인 hidden unit은 $\boldsymbol{h}$로 표기할 것이다. 지금까지 RBM의 구조에 대해서 살펴보았다. RBM은 확률 분포를 학습하기 위해 만들어졌다. RBM이 주어진 데이터를 제대로 학습했다면 sampling을 통해 얻은 visible layer의 데이터가 원래 데이터와 거의 같아야 한다.
모델이 제대로 학습되었는지 확인을 하기 위해서는 여타 다른 Deterministic model들과 동일하게 loss function과 같은 하나의 '지표'가 존재해야한다. RBM에서는 이 loss function을 MLE로 사용하며, 현재 데이터들을 가지고 얻은 확률값이 최대가 되는 지점을 찾는 것이다. 만약 학습이 제대로 잘 되었다면 Likelihood는 최대가 될 것이다. 위에서 볼츠만 머신의 상태 $x$에 대한 에너지 함수를 $E(x)$라고 언급했다. 그리고 에너지 함수를 통해 결합 확률 분포 $P(x)$를 정의하였다. RBM 역시 볼츠만 머신과 동일하게 다음과 같이 결합 확률 분포 $P(x)$를 정의할 수 있다.
\[ P(x) = \frac{1}{Z} \exp(-E(x)) \]
\[ where \ \ Z = \sum_x \exp\{ -E(x)\} \]
우리는 상태 $x$를 visible units $\boldsymbol{v}$과 hidden units $\boldsymbol{h}$로 구성한다고 언급했다. 하지만 우리가 관찰할 수 있는 것은 visible units $\boldsymbol{v}$에 대한 것 뿐이다. 그렇기에 다음과 같이 visible units $\boldsymbol{v}$의 확률 분포를 결정할 수 있다.
\[ p(v) = \sum_h p(v, h) = \sum_h \frac{\exp(-E(v,h))}{Z} \]
\[ where \ \ Z = \sum_v \sum_h \exp\{ -E(v, h)\} \]
기존의 상태 $x$를 $v$와 $h$로 분리해 수식을 정리하였다. 하지만 해당 식으로 전개하기엔 수식이 너무 복잡하므로 다음과 다음과 같이 치환을 한다. 결합 확률 분포이기에 $Z=1$임을 알 수 잇다.
\[ p(v) = \frac{1}{Z^{\prime}} \exp(-F(v)) \]
\[ where \ \ F(v) = -\log \sum_h \exp(-E(v, h)) \]
\[ and \ \ Z^{\prime} = \sum_v \exp(-F(v)) \]
$F(\cdot )$은 Free Energy라고 부른다고 한다. RBM 역시 BM과 동일하게 하나의 에너지 기반 모형이기 때문에 다음과 같이 에너지 함수를 통해 서술될 수 있다.
\[ E(v, h) = -b^T v - c^T h - v^T Wh \]
$b$는 visible unit의 bias를 의미하며 input data의 inherent property를 설정해주는 부분이다, $c$는 hidden layer의 bias를 의미하며, hidden data의 inherent property를 설정해주는 부분이다. 만약 visible layer의 node 수가 $d$개이고, hidden layer의 node 수가 $n$개라고 가정하면, 각각의 차원은 $v, b \in \mathbb{R}^{d\times 1} $, $h, c \in \mathbb{R}^{n \times 1} $ 가 된다. BM의 경우 각 Layer끼리의 연결성도 존재해 복잡한 에너지 함수를 가지고 있었지만, RBM의 경우 BM에 비해 상대적으로 간단해진 것을 확인할 수 있다.
loss function
다시말하자면 RBM에게 학습이란 Contrastive Divergence(CD)를 줄이는 것이다. CD는 visible layer에 데이터를 입력해주고, hidden layer의 node 값을 샘플링한 후 다시 visible layer의 데이터를 다시 예측하도록 하는 과정에서 처음 주어진 visible layer와 다시 획득한 visible layer간 얼마나 차이가 있는지를 의미한다. 만약 $W$와 hidden layer의 bias가 제대로 학습되었다면 hidden unit을 잘 sample 해줄 수 있을 것이고, 그렇다면 다시 획득한 visible layer의 데이터는 원래 데이터와 일치할 것이다.
sampling
위에서 우리는 데이터를 잘 sampling한다고 언급했다. 그렇다면 visible layer 또는 hidden layer의 데이터는 어떻게 sampling할 수 있을까? RBM에서는 Markov Chain Monte Carlo 의 한 종류인 Gibbs sampling을 사용한다고 한다. Gibbs sampling은 두개 이상의 확률 변수의 결합 확률 분포로부터 표본을 생성하는 확률적 알고리즘으로, $n$개의 확률변수 $(X_1, \cdots, X_n)$의 결합 확률 분포 $p(x_1, \cdots, x_n)$로 부터 $k$개의 표본 $X$를 얻으려고 할 때 Gibbs sampling은 다음과 같이 작동한다.
1. 임의의 $X^{(0)} = (x_1^{(0)}, \cdots , x_n^{(0)})$을 선택한다.
2. 각 변수 $x_1, \cdots , x_n$에 대하여, 현재의 값을 기반으로 한 새로운 값을 조건부 확률 분포 $p(x_i^{(t)}|x_1^{(t)}, \cdots, x_{i-1}^{(t)}, x_{i+1}^{(t-1)}, \cdots, x_n^{(t-1)} $에서 표집한다.
3. $X^{(t)} = (x_1^{(t)}, \cdots, x_n^{(t)})$를 $X$에 추가한다.
RBM은 확률 분포를 정의할 때 에너지 함수와 exponential 함수를 사용한다. 그로 인해 computional complexity가 exponential이 된다. 우리가 모든 step을 다 수행하여 gradient를 계산하게 되면 엄청난 시간이 소요된다. 그래서 RBM 논문에서는 '어짜치 정확하게 converge한 distribution이나, 중간에 멈춘 distribution이나 방향성은 똑같지 않을까?' 라는 생각을 하게된다. 완벽한 gradient 대신, Contrastive Divergence를 통해 연산량을 줄인 것이다. Hinton이 제안한 이후 d이 알고르즘이 log likelihood의 local optimum으로 converge한다는 이론적 결과까지 증명되었다.
RBM을 구현한 코드는 여기를 참고하길 바란다.
'Deep Learning' 카테고리의 다른 글
| 퍼셉트론(Perceptron) (0) | 2022.05.06 |
|---|---|
| Object Function, Cost Function, Loss Fuction (3) | 2022.04.28 |
| [Deep Learning] RBF : Radial basis function (0) | 2022.03.21 |
| Multi-layer Perceptron (MLP) (0) | 2021.06.21 |