Multi-layer Perceptron (MLP)

Multi-layer Perceptron (MLP)

단층 퍼셉트론은 Linear - model 이다. ( logistic, Multiple linear regression, ...) 선형 모델은 식의 복잡도가 낮은 것이 한계점이다. 복잡도가 낮기 때문에 좋은 예측 성능을 찾아내기 힘들다. (단, 설명변수와 종속변수 간의 관계가 선형이 아닐경우) 기존의 단층 퍼셉트론에서 XOR을 할 경우 모델을 정확하게 구분하기에 어려움을 겪었다.

XOR

선을 하나만 그어서는 문제가 발생하기 때문에 선을 여러개를 그어서 합치자 라는 것이 Multi-layer Perceptron (MLP)의 개념이라고 할 수 있다. 복잡한 문제를 바로 풀 수 없다면 분해하여 각각을 구분하는 것이다.

MLP

왼쪽 하단의 점을 구분할 수 있는 퍼셉트론을 하나 만들고, 오른쪽 상단에 있는 점을 구분할 수 있는 퍼셉트론을 만들어 이 둘을 적당히 잘 조합하여 선 사이에 있는 점과 바깥의 점을 구분할 수 있을 것이다. 선을 어떻게 조합하냐에 따라서 새로운 비선형 모델을 만들 수 있다.

 

logistic, decision, MLP 차이

MLP

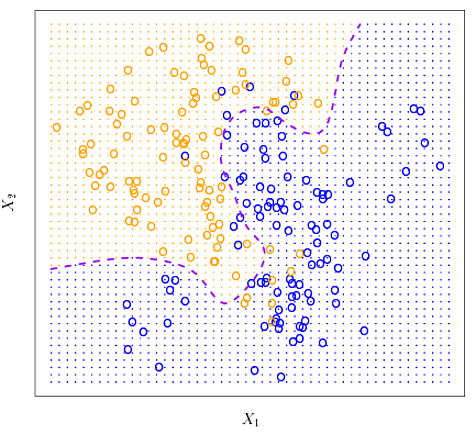
Logistic 은 선은 단 하나만 존재할 수 있다 하지만 기울기에 대해서는 제약이 없다. Decision Tree는 선의 개수는 제한이 없지만 어떤 값보다 크다 작다라는 설명력을 가지려면 축에 대해서 수직으로 작용하여야 한다. 그리고 MLP는 사전에 선의 개수를 조절할 수 있다.(hidden layer, node 수를 조정하면서 가능) 선의 방향에 대해서도 아무런 제약이 없다.

$ y = \Sigma_{i}^{p}w_{p}^{(2)}h_{p}$ 

Classification

$y_{j}$  soft max function

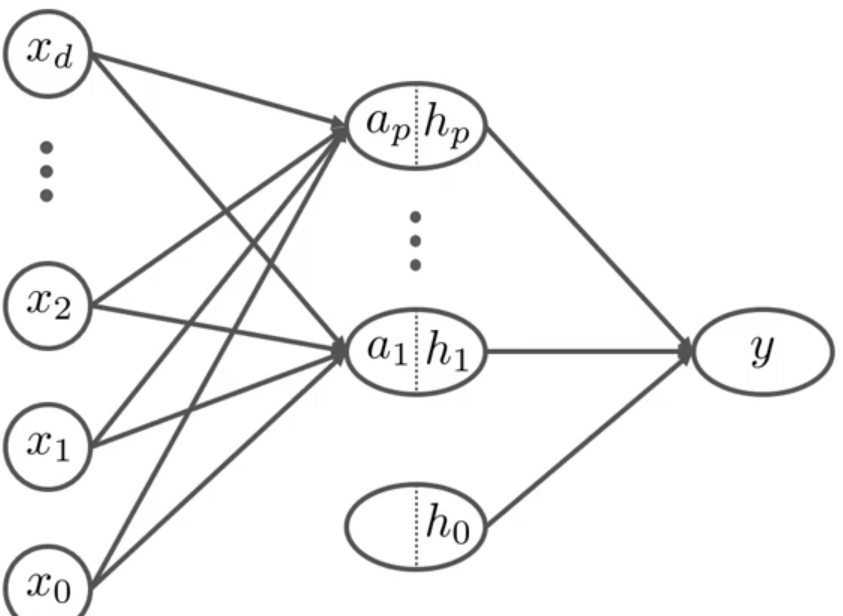
input layer와 Hidden layer, Output layer로 구분되어 있다. ( hidden layer가 여러개라면 딥러닝 구조로 들어간다)

hidden layer의 각 하나의 node는 퍼셉트론을 의미하고 퍼셉트론 여러개가 합쳐진 MLP라고 할 수 있다. 각각의 퍼셉트론은 각자 자기 나름대로 input을 취합하여 결과값을 도출해낸다. ( 각각의 가중치는 다 다르다 )

 

Classification 인 경우는 output node는 Class의 수 만큼 출력되게 된다. (one hot encoding 방식으로 출력된다)

$w_{p}^{(1)} $ 의 의미는 input 과 hidden node를 연결하는 가중치로 표현된다.

hidden node 개수가 많아질수록 조금더 복잡한 모형을 구할 수 있다

 

XOR problem revisited

XOR 에서는 일반적인 퍼셉트론의 식으로는 구분을 하기가 어렵기 때문에 MLP를 사용한다. 처음으로 왼쪽 아래 파란 원만 구분할 수 있는 선을 그린다. (그림 1) $a_{1} = x_{1}+x_{2} - {3 \over 2} $ 를 가지고 $H_{1}$ 을 구하게 된다. ( activate function은 step function이다.) 두번째로는 오른쪽 상단의 파란 원만 구분할 수 있도록 선을 그린다. (그림 2)

$a_{2} = x_{1} + x_{2} - {5 \over 2} $ 를 가지고 $H_{2}$를 구하게 된다. 좌표 축을 h1, h2로 바꾸어 그래프를 그리면 그림 3과 같이 나온다. 

그림 1

그림 2

그림 3 

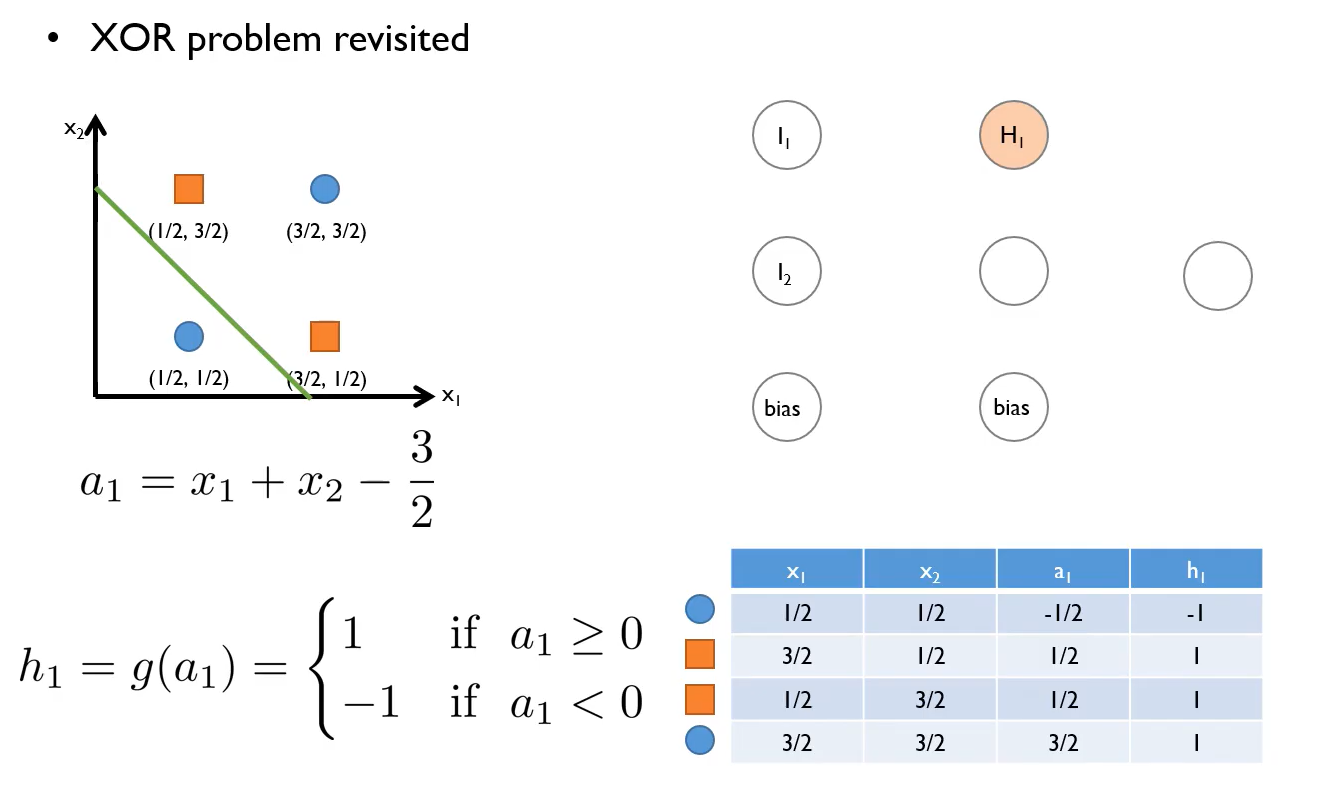
처음 그래프에서는  선형적으로 분리가 불가능(non - Separable) 하였지만, 퍼셉트론에 의해 분리된 공간상에서는 선형으로 분리가 가능(Separable)하게 되었다. 이것이 MLP의 원리이다.

 

---

강필성 교수님 수업자료를 참고하여 작성하였습니다.