Contents
조건부 확률(Conditional Probability)
본 강의에서는 조건부 확률(Conditional Probability)에 대해서 알아보고, 조건부 확률에서 나오는 용어들이 어떤 것들이 있는지, 이 용어들의 정의에 대해서 알아본다.
Independent
독립은 조건부 확률을 다루기 위해서는 필수적으로 알아야될 개념이다. 확률에서 나오는 독립은 일반적으로 생각하는 독립과는 다를 수 있다. 일반적으로 다루는 독립은 완전히 독립적으로 떨어져 있는 것을 의미하지만, 여기에서 나오는 독립은 조금 다른 개념이다.
두 사건 A, B가 있다고 하자. 이때 다음과 같을 때 이를 독립이라고 한다.
\[ P(A \cap B) = P(A)P(B) \]
우리는 이전 글에서 서로소(disjoint)에 대해서 알아보았다. 서로소는 서로 겹치지 않는 것을 의미하고, A와 B가 서로소인 사건이라면, A가 발생했을 때 B는 발생할 수 없다. 반면에, A와 B가 독립이라면, A의 발생은 B의 발생여부에 대한 그 어떠한 영향도 끼치지 않는다.
\[ P(A \cap B) = P(A)P(B), P(B \cap C) = P(B)P(C), P(C \cap A) = P(C)P(A) \]
\[ P(A \cap B \cap C) = P(A)P(B)P(C) \]
모두 성립할 때 사건 A, B, C는 독립이다. 먼저 각각의 쌍들이 독립인지 확인하고 A, B, C의 교집합도 독립임을 확인하여야 한다.
Newton-Pepys Problem
Newton-Pepys Problem은 1693년에 나온 매우 유명한 예제 중 하나다. 공정한 주사위를 가지고 있을 때, 다음중 어떤 경우가 발생할 확률이 가장 높은가? (a) 6개의 주사위 적어도 한 개가 '6'인 경우, (b) 12개의 주사위 중 적어도 두 개가 '6'이 나온 경우 (c) 18개의 주사위 중에서 적어도 세 개가 '6'이 나온 경우
'적어도 몇 개'라는 표현이 나오면 합집합을 생각해야 된다. 전체 전체 집합에서 여집합을 빼면서 계산할 수 있기 때문이다. 이때 P(A)는 전체 확률에서 모두 '6'이 나오지 않을 확률을 의미한다. 이는 모든 주사위가 '6'이 나올 확률을 뜻하기도 한다. P(B)는 12개의 주사위를 던졌을 때, '6'이 한 번도 나오지 않을 확률과 한 번만 나올 확률을 전체 확률에서 빼면 된다. 마지막 P(C)는 18개의 주사위를 던졌을 때, '6'이 한 번도 나오지 않을 확률과 한 번 혹은 두 번만 나올 확률을 빼면 된다.
\[ \begin{equation} \begin{split} P(A) & = 1 - \left( \frac{5}{6} \right)^6 \approx 0.665 \\ \\ P(B) & = 1 - \left\{ \left(\frac{5}{6}^{12} \right) + \frac{1}{6} \times \left( \frac{5}{6} \right)^{11} \times 12 \right\} \approx 0.619 \\ \\ P(C) & = 1 - \sum^2_{k=0} \begin{pmatrix} 18 \\ k \end{pmatrix} \left( \frac{1}{6} \right)^k \left( \frac{5}{6} \right)^{18-k} \approx 0.597 \end{split} \end{equation} \]
조건부 확률에서 사용하는 독립 개념에 대해서 알아 보았으니 이제 조건부 확률이 어떤 것인지 알아보자. 조건부 확률은 새로운 정보를 얻었을 때, 기존의 믿음/불확실성(uncertainty)을 어떻게 업데이트 하는가에 대한 내용이다. 즉, 주어진 사건이 일어났다는 가정 하에 다른 한 사건의 일어날 확률을 의미한다.
\[ P(A|B) = \frac{P(A \cap B)}{P(B)}, \quad (P(B) > 0) \]
사건 B가 주어졌을 때, 즉, 발생했을 때 사건 A가 발생할 확률을 의미한다. 조건부 확률을 통해 아래와 같은 다양한 정리를 도출할 수 있다. 가장 대표적인 예가 베이즈의 정리(Bayes' Theorem)이며, 이후 베이지안 통계를 다룰 때 매우 중요하다.
\[ (1) \quad P(A \cap B) = P(B)P(A|B) = P(A)P(B|A) \]
\[ (2) \quad P(A_1, A_2, ..., A_n) = P(A_1)P(A_2|A_1)P(A_3|A_1, A_2)...P(A_n|A_1, ..., A_{n-1})\]
\[ (3) \quad \begin{equation} \begin{split} P(A|B) & = P(B)P(A|B) = P(A)P(B|A) \\ \\ P(A|B) & = \frac{P(A)P(A|B)}{P(B)} \end{split} \end{equation} \]
베이즈 공식을 보면 기존의 수식을 바꿔가며 새로운 수식을 도출해 값을 계산하고 있다. 왜 이렇게 변화하면서 값을 바꾸어 계산해야 될까? 사건 A를 사용자가 호텔에 방문할 확률이라고 하자. 사건 B는 웹사이트에 있는 호텔 광고를 보고 클릭할 확률이라 하자. 호텔 광고를 클릭했을 때 사용자가 호텔을 방문할 확률은 P(A|B)가 된다. 이를 구하기 위해서는 모든 광고를 찾아 확률값을 계산하고 이를 계산하여야 한다. 쉬운 일이 아니다. 반면에 $\frac{P(B|A)P(A)}{P(B)}$로 계산하게 되면, 사용자가 호텔에 방문했을 때 광고를 클릭하고 올 확률은 호텔에서 조사하면 그만이다. 이렇게 문제를 바꾸면 단순한 문제가 된다.
Conditioning Continued, Law of Total Probability
본 강의에서는 전체 확률의 법칙을 이해하고 문제풀이에 적용할 수 있으며, 조건부 독립의 개념을 이해하고 전체 확률의 법칙(Law of Total Probability), 조건부 확률, 사전확률과 사후확률(Prior, Posterior Probability), 조건부 독립(Conditional independence)에 대해서 다룬다. 사전확률과 사후확률은 위에서 다룬 베이즈 정리에 매우 필수적인 개념이기에 숙지하여야 한다.
Law of Total Probability
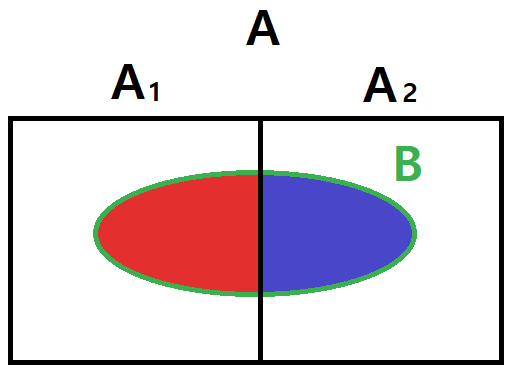
전체 확률의 법칙 혹은 전확률 정리는 조건부 확률과 관계된 법칙 중 하나다. 조건부 확률로부터 조건이 붙지 않은 확률을 계산할 때 사용할 수 있으며, 베이즈 정리 공식의 일부에 전확률 정리 공식이 들어간다. 전체 사건을 A라고 한다면, 사건 $B$가 발생할 확률은 아래와 같다.
\[ \begin{equation} \begin{split} P(B) & = P(B \cap A) \\ \\ & = P(B \cap A_1) + P(B \cap A_2) \\ \\ & = P(B|A_1)P(A_1) + P(B|A_2)P(A_2) \end{split} \end{equation} \]
이 수식을 위 베이즈 정리로 유도되는 수식에 대입하면 아래와 같은 수식을 도출할 수 있다.
\[ \begin{equation} \begin{split} P(A_1|B) & = \frac{P(B \cap A_1)}{P(B)} \\ \\ & = \frac{P(B|A_1) P(A_1)}{P(B)} \\ \\ & = \frac{P(B|A_1) P(A_1) }{ P(B|A_1)P(A_1) + P(B|A_2)P(A_2)} \end{split} \end{equation} \]
위 수식은 사건 $B$가 발생했을 때 사건 $A_1$이 발생할 확률을 의미한다. 이는 전체 사건 $B$가 발생할 확률에서 $A_1$가 발생할 확률을 계산하는 문제로 이해할 수 있다.
Example1
카드 한 벌에서 무작위로 두 장을 뽑았을 때 두 장이 모두 에이스일 확률을 구해보자. 둘다 에이스인 사건을 A라고 하고, 에이스가 주어졌을 때를 사건 B라고 하자. 첫 번째 뽑은 카드가 에이스일 때 두 번째 카드도 에이스일 확률은 아래와 같이 수식으로 계산이 가능하다.
\[ P(A|B) = \frac{P(A \cap B)}{ P(B) } \]
\[ \frac{ _4C_2 / _{52}C_2}{1 - _{48}C_2 / _{52}C_2} = \frac{1}{33} \]
$ _4C_2 / _{52}C_2$는 52장 중 A를 두 장 뽑을 확률을 의미한다. 분모의 $1 - _{48}C_2 / _{52}C_2$는 첫 번째 카드가 에이스일 확률을 의미한다. 에이스가 아닐 확률에 여사건을 계산한 것이다.
그렇다면 첫 번째 카드를 스페이드 에이스로 뽑았을 때 다음 뽑은 카드도 에이스일 확률은 어떻게 구할 수 있을까?
\[ \frac{ 3 }{ 51 } = \frac{1}{17} \]
카드가 두 장 있다고 할 때 첫 번째 카드는 스페이드 에이스로 고정되어 있다. 그렇다면 두 번째 카드가 에이스일 확률은 $\frac{3}{51}$ 이다. 쉽게 계산할 수 있다. 위 수식처럼 분모를 구하고 분자를 계산하는 형태로도 가능하지만, 복잡하게 계산되기 때문에 직관적으로 이해하는 것이 중요하다.
Example2
인구의 1%가 걸리는 병이 있고, 이 병의 검사 결과가 95%의 정확도를 갖고 있다고 하자. 검사가 양성으로 나왔을 때, 실제 이 병에 걸렸을 확률은? 이때, 병에 걸릴 확률에 대한 값을 $P(A)$라고 하고, 걸리지 않을 확률을 $P(A^C)$라 하자.
\[ \begin{equation} \begin{split} P(A|B) & = \frac{P(A \cap B)}{P(B)} \\ \\ & = \frac{P(B|A) P(A)}{P(B)} \\ \\ & = \frac{P(B|A)P(A)}{P(B|A)P(A) + P(B|A^C)P(A^C) } \\ \\ & = \frac{0.95 * 0.01}{0.95 * 0.01 + 0.05*0.99} \\ \\ & = 0.16 \end{split} \end{equation} \]
사전에 주어진 확률은 $P(A)=0.01$이 되고, 구하고자 하는 값은 $P(A|B)$이다. 검사의 정확도는 95%이기 때문에 $P(B|A) = P(B^C|A^C) = 0.95$가 될 수 있다. 우리는 검사가 양성이 나올 확률은 $P(B)$로 표기할 수 있는데, 이는 우리가 알지 못하는 값이다. 따라서 전체 확률의 법칙을 통해 $P(B)$를 $P(B|A)P(A) + P(B|A^C)P(A^C)$로 나누어 계산하는 것이다. $P(B|A^C)$에 대한 값은 다루지 않았으나, $P(B^C|A^C)=0.95$임을 알고 있기 때문에 $0.05$로 쉽게 찾을 수 있다.
해당 문제의 가정은 다른 정보 없이 단순히 인구의 1%가 해당 병을 가지고 있다는 것만 다루고 있다. 즉, 사전에 얻은 정보가 하나 뿐인 것이다. 만약 새로운 정보가 유입되는 경우 확률값은 달라진다. 예를 들어, 해당 병의 고유한 증상이 있거나 하는 정보(확률)를 얻는다면 확률은 달라진다. 그러나 이 경우에도 동일하게 베이즈 정리를 쓴다는 것은 변함이 없다. 이때의 사전확률(Prior)은 $P(A)$를 의미하고, 사후확률(Posterior)은 사건 B가 발생했을 때의 확률 즉, $P(A|B)$가 된다. 혼동하지 말자.
Conditional Independence
조건부 독립은 'A와 B는 조건 C하에서 독립이다'라는 것이다. 즉, 어떠한 조건 하에서 A와 B가 독립이 된다는 것을 의미한다. 이를 수식적으로 나열하면 아래와 같다.
\[ \begin{equation} \begin{split} P(A \cap B | C ) =& \frac{ P(A \cap B \cap C)}{P(C)} \\ \\ \text{iff } \frac{P(A \cap B \cap C}{P(C)} =& \left( \frac{P(A \cap C)}{P(C)} \right) \left( \frac{P(B \cap C)}{P(C)} \right) \\ \\ \text{iff } P(A \cap B \cap C) =& \frac{P(A \cap C) P(B \cap C)}{P(C)} \\ \\ \text{iff } \frac{P(A \cap B \cap C)}{P(B \cap C)} =& \frac{P( A \cap C)}{P(C)} \\ \\ \text{iff } P(A|B \cap C) =& P(A|C) \end{split} \end{equation} \]
조건부 독립이면, 독립일 수도 있고 독립이 아닐 수도 있다. 또한, 독립이라고 무조건 조건부 독립이 되지 않을 수도 있다.
'Mathematics > Statistics' 카테고리의 다른 글
| [Statistics] Power Law Distribution (0) | 2022.09.27 |
|---|---|
| [Statistics] Probability 110 - Probability and Counting (0) | 2022.09.06 |
| [Statistics] AIC(Akaike information criterion) (0) | 2022.05.25 |
| [Statistics] 구조방정식모델(structural equation model)의 모든 것 (6) | 2022.03.29 |
| [Statistics] F-test (0) | 2022.03.23 |