[Statistics] Power Law Distribution

 

 

Power Law Distribution은 다양한 이름으로 불린다. Long Tail Distribution으로도 들어본 적 있을 것이다. 이 그래프는 사회의 현상을 가장 잘 매핑할 수 있는 함수이며, 어떤 식으로 유도되는지 알아보자. 

 

Power Law Distribution은 Real-World 네트워크 구조를 가장 잘 설명할 수 있다고 한다. 이 분포는 오른쪽으로 긴 꼬리를 가진 형태를 띄고 있어서 가독성이 많이 떨어진다. 이때 Power Law Distribution에 아래와 같은 Log-Log 수식을 취하면 Log-Log plot을 그릴 수 있고, 유의미한 패턴을 찾을 수 있다. 

$$\begin{array}{rl}\ln p(x)& =-\alpha \ln x+c\\ \\ p(x)& =C{x}^{-\alpha }\end{array}$$

 

이때 $2<\alpha <3$인 경우 항상 1보다 큰 값을 가지게 된다. Pow Law Distribution이 어떻게 유도되는지 알기 위해서는 먼저, Complementary Cumulative Distribution Function (CCDF)를 알고 있어야 한다. CCDF는 Cumulative Distribution Function (CDF)를 통해 계산되며, CCDF를 파레토 법칙(Pareto's Law)이라고 부른다. 모델을 학습할 때 학습 데이터와 테스트 데이터를 분할하는 경우 파레토 법칙을 통하여 8:2로 분할해 사용한다. 

$$\begin{array}{rl}P(X\ge x)& ={\int }_x^{\mathrm{\infty }}p(x)dx=C{\int }_x^{\mathrm{\infty }}{x}^{-\alpha }dx\\ \\ & =\frac{C}{\alpha -1}{x}^{-(\alpha -1)}\end{array}$$

 

CDF를 이해하기 위해서는 또 Probability Density Function (PDF)를 알고 있어야 한다. PDF는 확률 밀도 함수로 확률 질량 함수(Probability Mass Function)과는 다르다. 이는 연속적인 변수의 분포를 나타내고 우리가 가장 많이 접한 함수 중 하나다. 이때 PDF에 $a$와 $b$사이의 면적을 측정하기 위해서는 적분을 사용하여야 하며, 아래와 같은 수식을 띈다.

$$\begin{array}{rl}P(a\le X\le b)& ={\int }_a^b{f}_X(x)dx\\ \\ f_X(x)& =\frac{d{F}_X(x)}{dx}\end{array}$$

$$f_X(x)\ge 0\text{ for all }x,F_X(x)={\int }_{-\mathrm{\infty }}^x{f}_X(u)du,{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{f}_X(x)dx=1$$

 

CDF는 PDF의 $P(X\le x)$의 값을 의미한다. CCDF는 반대로 $P(X\ge x)$의 값을 의미하며, 우리가 계산한 값에서 1을 빼주면 쉽게 계산이 가능하다. 위 수식으로 유도하는 경우 $a=-\mathrm{\infty },b=x$로 설정하고, 도출되는 값을 1에서 빼면 수식이 동일하다. 

$$\begin{array}{rl}1-P(-\mathrm{\infty }\le X\le x)& =P(X\ge x)\\ \\ & ={\int }_x^{-\mathrm{\infty }}p(x)dx\\ \\ & =C{\int }_x^{-\mathrm{\infty }}{x}^{-\alpha }dx\\ \\ & ={\left[\frac{C}{-\alpha +1}{x}^{-\alpha +1}\right]}_x^{\mathrm{\infty }}\\ \\ & =\frac{C}{\alpha -1}{x}^{-(\alpha -1)}\end{array}$$

위 수식의 경우 C라는 값이 하나 더 생기기 때문에, C를 $x$에 관련된 수식으로 변경하여 $p(x)$ 수식을 조금더 간단하게 표현해보자. 

$$p(x)=C{x}^{-\alpha }\text{ for }k\ge k_{\text{min}}$$

$$\begin{array}{rl}{\int }_{k_{\text{min}}}^{\mathrm{\infty }}p(k)dk=1& ={\left[\frac{C}{-\alpha +1}{k}^{-\alpha +1}\right]}_{k_{\text{min}}}^{\mathrm{\infty }}=1\\ \\ & \frac{C}{\alpha -1}{k}_{\text{min}}^{-\alpha +1}=1\\ \\ & C=(\alpha -1){\left(\frac{1}{k_{\text{min}}}\right)}^{-\alpha +1}=\left(\frac{\alpha -1}{k_{\text{min}}}\right){\left(\frac{1}{k_{\text{min}}}\right)}^{-\alpha }\\ \\ \therefore p(k)& =\left(\frac{\alpha -1}{k_{\text{min}}}\right){\left(\frac{k}{k_{\text{min}}}\right)}^{-\alpha }\end{array}$$

위 수식을 기반으로 CCDF를 도출해보자.

$$\begin{array}{rl}P(K\ge k)& ={\int }_k^{\mathrm{\infty }}p(y)dy\\ \\ P(K\ge k)& =\frac{C}{\alpha -1}{k}^{-(\alpha -1)}\because P(X\ge x)=\frac{C}{\alpha -1}{x}^{-(\alpha -1)}\\ \\ & =\left(\frac{1}{\alpha -1}\right)\left(\frac{\alpha -1}{k_{\text{min}}}\right)\left({\frac{1}{k_{\text{min}}}}^{-\alpha }\right)k^{-(\alpha -1)}\therefore C=\left(\frac{\alpha -1}{k_{\text{min}}}\right){\left(\frac{1}{k_{\text{min}}}\right)}^{-\alpha }\\ \\ & ={\left(\frac{1}{k_{\text{min}}}\right)}^{-\alpha +1}{k}^{-(\alpha -1)}\\ \\ & ={\left(\frac{k}{k_{\text{min}}}\right)}^{-\alpha +1}\\ \\ \therefore P(K\ge k)& ={\left(\frac{k}{k_{\text{min}}}\right)}^{-\alpha +1}\end{array}$$

이때 $x$가 1로 주어진다면, 1보다 많이 발생할 확률을 의미한다. 예를 들어, 지진이 1회 이상 일어날 확률을 통해서 몇 년 만에 지진이 일어날지 예측하는 등의 실제 real-world의 사건을 예측할 수 잇다. T 시점을 예측하고자 하는 경우 아래의 수식을 통해 도출이 가능하다.

$$\tau =\frac{T}{nP(X\ge x)}=\frac{T}{n}{\left(\frac{x}{x_{\text{min}}}\right)}^{\alpha -1}$$ 

$$\log \tau =\log Tn+(\alpha -1)(\log x-\log x_{\text{min}}$$ 

$$\log x=\left(\frac{1}{\alpha -1}\right)\log \tau +C$$ 

$$\text{where }C=\log x_{\text{min}}-\left(\frac{1}{\alpha -1}\right)\log \frac{T}{n}$$ 

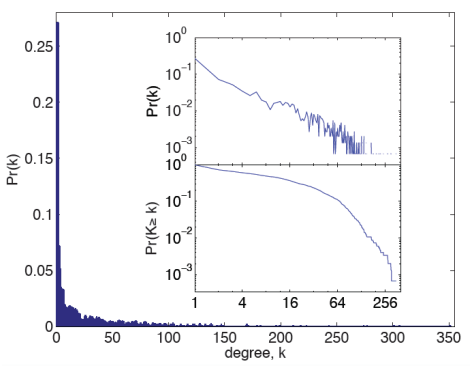
아래의 그림을 통해 $\tau$ 즉, 시간 동안 얼마만큼의 사건이 발생할 것인지 수식을 도출할 수 있을 것이다. 오른쪽 그림의 경우 real-world 데이터에 이를 적용한 그래프를 나타낸다.