Contents
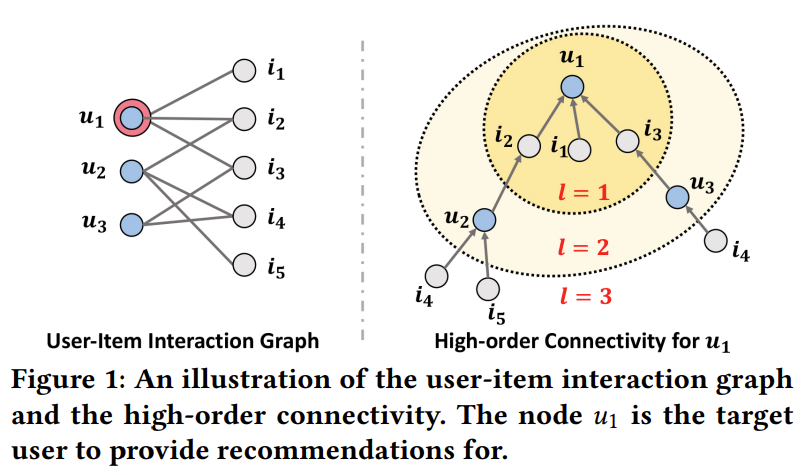
Neural Graph Collaborative Filtering (NGCF)는 기존의 협업 필터링(Collaborative Filtering)이 고차-연결성(High-Order Connectivity)을 고려하지 못한다는 단점을 극복하고자 그래프를 협업 필터링에 도입 시킨 기법이다. 전통적인 협업 필터링은 user-item interaction만을 고려하게 된다. 대표적인 Neural Collaborative Filtering (NCF)를 생각해보면 사용자 ID와 제품 ID를 내적하거나 연결(Concatenate)하여 사용자의 제품에 대한 구매 확률을 도출한다. 그렇기 때문에 제품과 다른 사용자 간의 관계 즉, 고차-연결성을 고려하지 못한다는 것이다. 예를 들어 $u_1 \leftarrow i_2 \leftarrow u_2 \leftarrow i_4$라는 그래프 상의 경로가 있을 때 그래프 구조에서는 이 경로를 모두 고려해 이웃 사용자들로부터 협력 신호(Collaborative Signal)을 제공 받아 $u_1$에게 $i_4$를 추천할 정보를 얻을 수 있지만, 기존의 협업 필터링에서는 어렵다는 것을 언급하고 있다. 이번 글에서는 NGCF의 코드를 리뷰하기 떄문에 논문의 자세한 내용은 여기를 참고하길 바란다.
Embedding Layer
먼저, 모델의 입력으로 사용하기 위해서는 사용자 ID와 제품 ID를 아래와 같이 임베딩(Embedding)하여야 한다.
\[ E = [ e_{u_1}, \cdots, e_{u_N}, e_{i_1}, \cdots, e_{i_M} ] \]
$e_u \in \mathbb{R}^d, \\ (e_i \in \mathbb{R}^d )$에서 $d$는 임베딩 크기를 의미하고, $e_u$와 $e_i$는 각각 사용자와 제품의 표현(Representation) 혹은 임베딩 벡터라고 부른다. 코드에서는 룩-업(Look-up) 테이블을 만들어, 인덱스에 위치하는 값을 추출한다.
import torch
from torch import nn
class NGCF(nn.Module):
def __init__(self, args, matrix):
super(NGCF, self).__init__()
self.num_users = args.num_users
self.num_items = args.num_items
self.latent_dim = args.latent_dim
self.device = args.device
self.user_emb = nn.Embedding(self.num_users, self.latent_dim)
self.item_emb = nn.Embedding(self.num_items, self.latent_dim)
self.num_layers = args.num_layers
GNN Layer
그래프에서는 Message Passing 단계가 필요하다. 해당 논문에서는 아래와 같은 수식을 통해 계산하고 있다.
\[ m_{u \leftarrow i} = \frac{1}{\sqrt{|\mathcal{N}_u| | \mathcal{N}_{i} |}} (W_1 e_i + W_2 (e_i \odot e_u)) \]
$|\mathcal{N}_u|$과 $|\mathcal{N}_i|$는 각각 사용자 노드와 제품 노드의 수를 의미한다. 추천 시스템에서 노드(Node)는 사용자와 제품을 의미하고, 간선(Edge)은 구매 여부 혹은 평점을 나타낸다. 위 수식을 행렬 형태로 변환하면 아래와 같이 표현할 수 있다.
\[ E^{(l)} = \text{LeakyReLU} ( (\mathcal{L} + I)E^{(l-1)}W^{(l)}_1 + \mathcal{L}E^{(l-1)} \odot E^{(l-1)}W^{(l)}_2 ) \]
코드를 실행시킬 때에는 행렬 형태로 변환하고 계산하기 때문에 계산의 효율성 문제로 행렬로 변환하고 사용한다.
class GNNLayer(nn.Module):
def __init__(self, in_feats, out_feats):
super(GNNLayer, self).__init__()
self.in_feats = in_feats
self.out_feats = out_feats
self.W1 = nn.Linear(in_feats, out_feats)
self.W2 = nn.Linear(in_feats, out_feats)
def forward(self, L, SelfLoop, feats):
# (L+I)EW_1
sf_L = L + SelfLoop
L = L.cuda()
sf_L = sf_L.cuda()
sf_E = torch.sparse.mm(sf_L, feats)
left_part = self.W1(sf_E) # left part
# EL odot EW_2, odot indicates element-wise product
LE = torch.sparse.mm(L, feats)
E = torch.mul(LE, feats)
right_part = self.W2(E)
return left_part + right_part
Build Matrix
그래프에서는 Laplacian Matrix, Adjacency Matrix, Diagonal Matrix 그리고 Feature Matrix를 사용한다. 논문에서는 각 행렬을 아래와 같이 표현하고 있다.
\[ \mathcal{L} = D^{-\frac{1}{2}} A D^{-\frac{1}{2}}\quad \text{and} \quad A = \begin{bmatrix} 0 & R \\ R^{\top} & 0 \end{bmatrix} \]
$\mathcal{L}$은 Laplacian Matrix를 나타내고, $A$는 Adjacency Matrix, $D$는 Diagonal Matrix를 의미한다. Feature Matrix는 모델의 입력으로 사용되며 0번째 $E$가 바로 Feature Matrix $X$가 된다. 수식에서 표현되는 $R \in \mathbb{R}^{M \times N}$은 user-item interaction matrix이다. $D^{-\frac{1}{2}}$를 Adjacency Matrix 양쪽에 곱한 이유는 정규화(normalization)를 해주기 때문이다.
def LaplacianMatrix(self, ratings):
iids = ratings['business_id'] + self.num_users
matrix = sp.coo_matrix((ratings['stars'], (ratings['user_id'], ratings['business_id'])))
upper_matrix = sp.coo_matrix((ratings['stars'], (ratings['user_id'], iids)))
lower_matrix = matrix.transpose()
lower_matrix.resize((self.num_items, self.num_users + self.num_items))
A = sp.vstack([upper_matrix, lower_matrix])
row_sum = (A > 0).sum(axis=1)
row_sum = np.array(row_sum).flatten()
D = np.power(row_sum, -0.5)
D = sp.diags(D)
L = D * A * D
L = sp.coo_matrix(L)
row = L.row
col = L.col
idx = np.stack([row, col])
idx = torch.LongTensor(idx)
data = torch.FloatTensor(L.data)
SparseL = torch.sparse.FloatTensor(idx, data)
return SparseL코드를 살펴보면 먼저, Rating Matrix $R$를 입력으로 받고, Sparse Matrix로 변환한다. 이때 user_id는 사용자 ID를 의미하고, business_id는 제품 ID를 의미한다. Upper Matrix는 $[ 0 \quad R]$로 표현된 행렬의 윗 부분을 만들기 위함이고, Lower Matrix는 그 아래의 행렬 부분을 만들기 위함이다. 그 후 vstack 함수를 사용해 합친 후 Diagonal Matrix와 Adjacency Matrix를 곱해 Laplacian Matrix를 생성한다. 여기서는 PyTorch를 사용하고 있기 때문에 마지막에 torch.spase를 사용해 numpy 를 pytorch 로 변환한다.
Model Prediction
NGCF 논문에서는 각 Layer 별로 출력된 Representation을 연결하고, weighted average, max pooling, LSTM 등과 같은 Layer를 추가로 연결해 최종 값을 도출한다.
\[ e^*_u = e^{(0)}_u || \cdots || e^{(L)}_u, \quad e^*_i = e^{(0)}_i || \cdots || e^{(L)}_i \]
\[ \hat{y}_{\text{NGCF}} (u, i) = e^{*\top}_u e^*_i \]
해당 코드에서는 MLP Layer를 사용하여 간단하게 구현해보았다.
def forward(self, uids, iids):
iids = self.num_users + iids
features = self.FeatureMatrix()
final_emb = features.clone()
for gnn in self.GNNLayers:
features = gnn(self.L, self.I, features)
features = self.leakyrelu(features)
final_emb = torch.concat([final_emb, features],dim=-1)
user_emb = final_emb[uids]
item_emb = final_emb[iids]
inputs = torch.concat([user_emb, item_emb], dim=-1)
outs = self.fc_layer(inputs)
return outs.flatten()
Build DataLoader
DataLoader를 만드는 것은 필수는 아니지만, Pytorch를 사용할 때에는 만들고 사용하는 것이 편리하다. 생각보다 간단하게 만들 수 있으니 되도록이면 사용하자.
from torch.utils.data import Dataset, DataLoader
class GraphDataset(Dataset):
def __init__(self, dataframe):
super(Dataset, self).__init__()
self.uid = list(dataframe['user_id'])
self.iid = list(dataframe['business_id'])
self.ratings = list(dataframe['stars'])
def __len__(self):
return len(self.uid)
def __getitem__(self, idx):
uid = self.uid[idx]
iid = self.iid[idx]
rating = self.ratings[idx]
return (uid, iid, rating)
def get_loader(args, dataset, num_workers):
d_set = GraphDataset(dataset)
return DataLoader(d_set, batch_size=args.batch_size, num_workers=num_workers)
Model Training
def graph_evaluate(args, model, test_loader, criterion):
output = []
test_loss = 0
model.eval()
with torch.no_grad():
for batch in tqdm(test_loader, desc='evaluating...'):
batch = tuple(b.to(args.device) for b in batch)
inputs = {'uids': batch[0],
'iids': batch[1]}
gold_y = batch[2].float()
pred_y = model(**inputs)
output.append(pred_y)
loss = criterion(pred_y, gold_y)
loss = torch.sqrt(loss)
test_loss += loss.item()
test_loss /= len(test_loader)
return test_loss, output
def graph_train(args, model, train_loader, valid_loader, optimizer, criterion):
best_loss = float('inf')
train_losses, valid_losses = [], []
for epoch in range(1, args.num_epochs + 1):
train_loss = 0.0
model.train()
for batch in tqdm(train_loader, desc='training...'):
batch = tuple(b.to(args.device) for b in batch)
inputs = {'uids': batch[0],
'iids': batch[1]}
gold_y = batch[2].float()
pred_y = model(**inputs)
loss = criterion(pred_y, gold_y)
loss = torch.sqrt(loss)
optimizer.zero_grad()
loss.backward()
optimizer.step()
train_loss += loss.item()
train_loss /= len(train_loader)
train_losses.append(train_loss)
valid_loss , outputs = graph_evaluate(args, model, valid_loader, criterion)
valid_losses.append(valid_loss)
print(f'Epoch: [{epoch}/{args.num_epochs}]')
print(f'Train Loss: {train_loss:.4f}\tValid Loss: {valid_loss:.4f}')
if best_loss > valid_loss:
best_loss = valid_loss
if not os.path.exists(args.SAVE_PATH):
os.makedirs(args.SAVE_PATH)
torch.save(model.state_dict(), os.path.join(args.SAVE_PATH, f'{model._get_name()}_parameters.pt'))
return {
'train_loss': train_losses,
'valid_loss': valid_losses
}, outputs이로써 학습에 필요한 코드는 전부 작성되었다. 그렇다면 이제 실제 학습을 해보자.
models = NGCF(args, d_train).to(args.device)
optimizer = optim.Adam(models.parameters(), lr = 1e-3)
criterion = nn.L1Loss()
results = graph_train(args, models, train_loader, valid_loader, optimizer, criterion)최적화함수를 호출하고, 손실함수를 정의한다. 그런다음 실제 학습을 수행하면 된다. 본 코드에는 BPRLoss를 사용하지 않았다. 사용한 데이터는 Yelp 데이터를 사용하였으며, 본 논문에서 사용하는 Implicit 관점이 아니라 Explicit 관점으로 코드를 작성했다. 다시 말해, 평점 3.5 점 이상인 경우 1로 표기하고, 3.5 미만인 경우 0으로 표기하였다. BPRLoss는 실제로 1인 값과 0인 값을 가지고 학습하는 것을 의미한다.
\[ L_{BPR} = - \underset{u=1}{\overset{M}{\sum}} \underset{i \in \mathcal{N}_u}{\sum} \underset{j \notin \mathcal{N}_u}{\sum} \text{ln} \sigma (\hat{y}_{ui} - \hat{y}_{uj}) + \lambda || E^{(0)}||^2 \]
실제 코드를 살펴보면 잘 학습되고 있는 것을 볼 수 있다. 전체 코드를 확인하고 싶으면 여기를 참고하면 된다.
'Python > Pytorch' 카테고리의 다른 글
| [Pytorch] pytorch에서 value count 하는 법 (0) | 2023.06.30 |
|---|---|
| [Pytorch] Transformer 구현하기 (0) | 2022.12.20 |
| [Pytorch] RuntimeError: CUDA error: CUBLAS_STATUS_NOT_INITIALIZED when calling (0) | 2022.12.05 |
| [Pytorch] BERT로 감성 분석하기. 기초 설명까지 (2) | 2022.12.03 |
| [Pytorch] Learning Rate Scheduler 사용하기 (0) | 2022.11.17 |