Contents
Neural Graph Collaborative Filtering (NGCF)의 제목을 보면 Neural Graph, Collaborative Filtering을 보고, Collaborative Filtering에 Graph를 접목시킨 Neural Network 임을 알 수 있을 것이다. 본 논문에서는 기존의 Collaborative Filtering의 문제점을 지적하고 이를 개선하기 위한 모델인 NGCF를 제안하였다. 본 논문을 읽기 위해서는 Collaborative Filtering에서 Matrix Factorization과 Graph Neural Network가 어떤 내용인지에 대한 선행 지식이 요구되며 이번 글에서는 깊게 다루지 않는다.
Introduction
Collaborative Filtering이란 사용자의 과거 기록에 기반하여 사용자가 선호할 만한 제품을 추천하는 방법으로, 대표적인 모델은 Matrix Factorication이 있다. Matrix Factorization은 행렬 분해라 부르며, 사용자-제품 행렬을 유저 행렬과 제품 행렬로 분해하고 내적(inner-product)을 통해 계산하는 방식이다. Matrix Factorizaton은 linear한 구조를 통해 계산하는 방식이지만, non-linear한 구조를 사용한 Neural Collaborative Filtering도 존재한다.
위에서 언급한 Matrix Factorization과 Neural Collaborative Filtering 등과 같은 모델은 다음과 같은 과정으로 모델을 학습하고 있다.
- Embedding: 사용자와 제품 정보를 One-hot Encoding으로 변형한 후 Embedding 과정을 통해 Latent Vector로 변환한다.
- Interaction model: Embedding을 통해 도출된 사용자 Latent Vector와 제품 Latent Vector를 내적 혹은 element-wise product 을 수행하여 사용자와 제품 간의 상호작용을 기반으로 결과를 도출한다.
이같은 방식은 우수한 성능을 발휘하고 있으나, 학습 과정을 살펴보면 1차원 구조의 사용자와 제품 간의 상호작용을 바탕으로 모델을 학습하고 있기에 사용자와 제품 간의 상호작용을 표현하기에는 다소 부족하다. 즉, 기존의 모델로는 사용자-제품 간의 상호작용에 잠재된 Collaborative signal을 명시적(Emplicit)으로 인코딩하지 않기 때문이다.

기존의 모델에서는 사용자와 제품 간의 관계를 단순히 Bipartite Graph 형태로 바라보고 있었다. 그러나 실제로는 단순히 Bipartite Graph를 가정하고 문제를 접근할 경우 어려울 수 있다. 왼쪽 그림과 같이 $u_1$는 $i_1, i_2, i_3$과 연결되어 있으나 $i_2$는 $u_2$과도 연결되어 있기에 이와 같은 관계에 대해서는 표현하지 못하기 때문이다. 따라서 본 논문에서는 오른쪽 그림과 같이 High-order connectivity를 이용한 Graph를 제안하였다. High-order connectivity는 경로(Hop) 길이가 1보다 큰 노드(Node)에서 $u_1$에 도달하는 경로를 의미하며, High-order connectivity에는 Collaborativei signal을 전달하는 semantic information이 포함되어 있다.
기존 방식과 같이 상호작용 행렬을 기반으로 모델링 할 경우 구현하는 것이 매우 복잡하기 때문에 본 논문에서는 Graph Mining에서 사용하는 Embedding Propagation에 영감을 받아 이를 사용하여 모델링한다. Embedding Propagation Layer에서는 상호작용하는 사용자(또는 제품)의 Embedding을 집계(Aggregating)하여 제품(또는 사용자)의 Embedding을 개선하며, Embedding Propagation Layer를 여러 층으로 쌓아서 Collaborative signal을 capture할 수 있다.
Methodology
NGCF는 Embedding Layer, Multiple Embedding Propagation Layer, Prediction Layer로 총 3 가지 Layer로 구성되어 있다. 각각의 Layer가 어떠한 역할을 하는지 알아보자.

Embedding Layer
일반적인 CF 기법과 동일하게 사용자와 아이템에 대한 Look-up Table을 만들어 입력으로 사용하며, 각각 $e_u \in \mathbb{R}^d, e_i \in \mathbb{R}^d$로 표현하며, 이때 d는 embedding size를 의미한다.
\[ \boldsymbol{E} = [ e_{u_1}, \cdots, e_{u_N}, e_{i_1}, \cdots, e_{i_M} ] \]
Embedding Layer는 end-to-end 방식으로 사용된다. 기존의 CF 기법의 사용자 Embedding과 제품 Embedding은 모델을 학습하기 위해 바로 내적을 수행하여 학습하지만, NGCF의 경우 사용자-제품 상호작용 그래프에 propagation하여 Embedding을 개선한다. 이와 같은 방식은 Embedding에 Collaborative Signal을 명시적으로 전달하기 때문에 기존 모델보다 효과적으로 Embedding할 수 있다.
Embedding Propagation Layers
Embedding Propagation Layer가 본 논문에서 가장 핵심적인 부분이며, Graph 구조를 따라 Collaborative signal을 Capture하고 사용자와 제품 Embedding을 개선하기 위해 메세지(Message)를 전달하도록 구성하였다.
First-order Propagation
First-order Propagation은 사용자가 직접 구매한 제품에 대한 상호작용 정보를 제공한다. 예를 들어 $u_1$가 $i_1, i_2, i_3$을 구매한 경우 $e_{u_1}$는 $e_{i_1}, e_{i_2}, e_{i_3}$를 입력으로 사용한다. 이를 기반으로 연결된 사용자와 제품 간의 Embedding Propagation을 수행하고, Message Construction과 Message Aggragation을 공식화(Formulate)한다. 그렇다면 Message Construction과 Message Aggragation은 무엇일까?
Message Construction
만약 사용자-제품 쌍 ($u, i$)가 있는 경우 제품 $i$가 사용자 $u$에게 전달할 메세지의 수식은 다음과 같이 표현할 수 있다.
\[ \text{m}_{u \leftarrow i} = f(e_i, e_u, p_{ui}) \]
이때 $\text{m}_{u \leftarrow i}$는 propagationg할 정보, 즉, message embedding을 의미하고, $f(\cdot)$은 message encoding function, $p_{ui}$는 얼마만큼 정보를 전달할 것인지를 조절하는 계수를 의미한다. 이를 구현하기 위해서 다음과 같은 수식을 활용한다.
\[ \text{m}_{u \leftarrow i} = \frac{1}{\sqrt{|N_u||N_i|}} (W_1 e_i + W_2 (e_i \odot e_u)) \]
$W_1, W_2 \in \mathbb{R}^{d' \times d} $는 weight matrix를 의미하며 $d'$는 transformation size를 의미한다. $\frac{1}{\sqrt{|N_u||N_i|}}$는 Laplacian norm을 의미하며, $N_u$와 $N_i$는 각각 사용자 $u$와 제품 $i$에 대한 first-hop의 이웃 수를 의미한다.
Message Aggregation
Message Aggregation은 Message Construction에서 계산된 정보들을 집계(aggregation)하며, 집계 함수는 다음과 같다.
\[ e_u^{(1)} = \text{LeakyReLU} (\text{m}_{u \leftarrow u} + \sum_{i \in N_u} \text{m}_{u \leftarrow i} ) \]
$e_u^{(1)}$는 첫 번째 Embedding Layer를 통과한 후 사용자 $u$의 representation을 의미한다. 본 논문에서는 LeakeReLU를 사용했는데, 이는 적은 양의 negative signal도 고려하기 위함이라고 한다. 추가적으로 $u$의 self-connection을 고려하기 위해 $\text{m}_{u \leftarrow u} = W_1 e_u$도 더해주었다. self-connection을 통해 원래 feature의 정보를 고려하는 것이다.
High-order Propagation
이러한 Embedding Propagation Layer가 여러 층으로 쌓이면 High-order Propagation이 된다. 우리는 이를 통해 high-order information를 찾을 수 있다. high-order connectivity는 사용자와 제품 간의 관련성을 추정하기 위해 필요한 Collaborative signal을 encoder하는 과정에서 매우 중요한 역할을 한다.
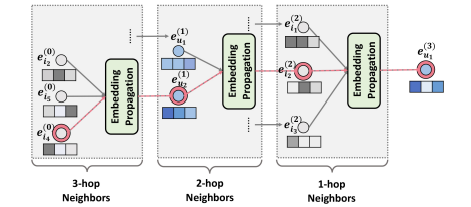
$l$ 만큼 쌓은 Embedding Propagtaion Layer는 $l$-hop neighbors로 부터 전파된 메세지를 제공 받는다. 위에서 정리한 메세지 집계 함수를 일반화하면 다음과 같다.
\[ e^{(l)}_u = \text{LeakyReLU}(\text{m}^{(l)}_{u \leftarrow u} + \sum_{i \in N_u} \text{m}^{(l)}_{u \leftarrow i} \]
\[ \begin{cases} \text{m}^{(l)}_{u \leftarrow i} = p_{ui} ( W^{(l)}_i e^{(l-1)}_i + W^{(l)}_2 (e^{(l-1)}_i \odot e^{(l-1)}_u )) \\ \\ \text{m}^{(l)}_{u \leftarrow u} = W^{(l)}_1 e^{(l-1)}_u \end{cases} \]
Propagation Rule in Matrix Form
위에서는 특정 사용자에 대한 수식을 다루어 보았다. 실제로 모델을 학습하기 위해서는 행렬 형태로 변환한 후 학습하게 되는데, 위 수식을 행렬 폼으로 변환하게 되면 다음과 같은 수식이 도출된다.
\[ E^{(l)} = \text{LeakyReLU}((\mathcal{L} + \mathrm{I}) E^{(l-1)} W_1^{(l)} + \mathcal{L} E^{(l-1)} \odot E^{(l-1)} W^{(l)}_2 ) \]
$E^{(l)} \in \mathbb{R}^{(N+M) \times d_l}$는 embedding propagation를 $l$ 번 수행한 후 사용자와 제품에 대한 representation을 의미한다. $\mathrm{I}$는 identity matrix를 의미하고, $\mathcal{L}$은 사용자-제품 그래프를 위한 Laplacian matrix를 의미한다. Laplacian matrix를 표현하면 아래와 같으며, 자세한 내용은 여기를 참고하길 바란다.
\[ \mathcal{L} = \mathrm{D}^{-\frac{1}{2}} \mathrm{A} \mathrm{D}^{-\frac{1}{2}}\ \text{and} \ \mathrm{A} = \begin{bmatrix} \mathrm{0} & \mathrm{R} \\ \mathrm{R}^{\mathrm{T}} & \mathrm{0} \end{bmatrix} \]
$\mathrm{R} \in \mathbb{R}^{N \times M}$은 사용자-제품 상호작용 행렬을 의미하며, $\mathrm{0}$은 영(zero) 행렬을 의미한다. $\mathrm{A}$는 인접(adjacency) 행렬, $\mathrm{D}$는 차수(Degree) 행렬을 의미한다.
Model Prediction
각기 다른 Layer에서 전파된 사용자 $u$의 representation은 ${e^{(1)}_u, \cdots, e^{(L)}_u$로 표현할 수 있다. 각 Layer의 representation은 서로 다른 메세지를 전달하기 때문에 서로 다른 Contribution을 한다. 본 논문에서는 이를 연결(Concatenate)하여 사용자와 제품에 대한 최종 Embedding을 구성한다.
\[ e^*_u = e^{(0)}_u|| \cdots || e^{(L)}_u, \ \ \ e^*_i = e^{(0)}_i || \cdots || e^{(L)}_i \]
|| 는 연결 연산(Concatenate operation)을 의미한다. 이렇게 함으로써, 초기 embedding을 조금 더 풍부하게 표현할 뿐만 아니라 L을 조정하면서 전파 범위를 제어할 수 있다. 연결하는 것 외에도 weighted average, max pooling, LSTM 등과 같은 기법을 사용해도 된다. 각기 계산된 $e^*_u, e^*_i$를 내적함으로써 $\hat{y}$를 예측할 수 있다. 이때 내적을 통해 연산하며 수식은 다음과 같다.
\[ \hat{y}_{\text{NGCF}}(u, i) = e^{*T}_u \cdot e^*_i \]
Optimization
본 논문에서는 모델을 최적화 하기 위해 BPR loss를 사용하며 수식은 다음과 같다.
\[ \text{Loss} = \sum_{(u, i, j) \in O} -\text{ln} \sigma (\hat{y}_{ui} - \hat{y}_{uj}) + \lambda || \Theta||^2_2 \]
$O={(u,i,j)|(u,i) \in \mathcal{R}^+, (u,j) \in \mathcal{R}^- }$에서 $\mathcal{R}^+$는 관측되는 상호작용을 의미하고 $\mathcal{R}^-$는 관측되지 않는 상호작용을 의미한다. 즉, Negative Sampling을 의미하며, 추천 시스템에서의 Negative Sampling에 대한 개념은 구매하지 않은 제품 중에서 Sampling하는 것을 의미한다. $\lambda$는 과적합(Overfitting)을 막기 위한 $L_2$ norm의 제어 변수로 이해하면 된다.
Experiments
본 논문에서 제안하는 NGCF의 성능을 측정하기 위해 Gowalla, Yelp, Amazon-Book 의 데이터를 사용하여 성능을 측정하였으며, 다음과 같은 총 3가지의 연구 질문에 초점을 맞추어 실험을 진행하였다.
RQ1. How does NGCF perform as compared with state-of-the-art Cf methods?
RQ2. How do different hyper-parameter settings affect NGCF?
RQ3. How do the representation benefit from the high-order connectivity?
RQ1) 본 논문에서 제안한 NGCF 모델이 기존의 state-of-the-art Cf method와 비교했을 때 우수한 성능을 보여주는지, RQ2) NGCF에는 Layer의 수, dropout 등 다양한 hyper-parameter가 존재하는데 이를 조절할 경우 어떠한 영향을 미치는지, RQ3) high-order connectivity가 representation에 어떠한 영향을 주는지 파악하는 것에 초점을 두었다.
Performance Comparison (RQ1)
NGCF의 모델의 성능을 측정하기 위해 아래와 같이 기존에 제안된 모델을 구축하여 recall과 ndcg를 사용하여 성능을 비교하였으며, 모든 경우에 우수한 성능을 보여주는 것을 확인하였다.

Study of NGCF (RQ2)
Layer의 수를 달리한 경우 Layer의 수가 3과 4일 때 가장 우수한 성능을 보이는 것을 확인하였으며, Layer가 1개 혹은 2개 인 경우에는 성능을 발휘하지 못한는 것을 확인하였다.
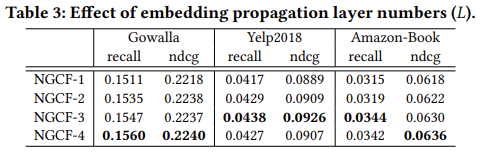
Yelp 데이터의 경우 Layer의 수가 3개를 넘어서는 경우 과적합(Overfitting)이 발생해 Layer의 수가 깊어질수록 오히려 성능이 저하되는 것을 확인할 수 있다. 이를 방지하기 위해 Dropout의 효과를 파악하기 위한 실험을 진행하였다. 본 논문에서는 message Dropout과 node Dropout 총 두 가지 Dropout의 효과를 파악하였으며, Dropout의 경우에는 node에 dropout을 취했을 때 성능이 훨씬 좋은 것을 확인하였다. .

다음으로는 NGCF와 MF를 Epoch에따라 Recall이 어떻게 변화하는지 확인하는 실험을 진행하였다. 아래의 그림에서 보이듯 NGCF가 MF보다 훨씬 빨리 수렴하는 것을 확인할 수 있다. 이는 NGCF의 propagation이 MF보다 효율적인 것을 의미한다. 본 논문에서는 모델의 용량도 MF에 비해 우수하다고 기술하고 있는데, 이를 따로 생각해본 바로는 사용자와 제품 간의 정보를 더 많이 함의하고 있다는 것으로 해석하였다.

Effect of High-order Connectivity (RQ3)
아래의 그림은 MF와 NGCF에서 3-order Connectivity까지 활용한 경우를 t-SNE로 표현하였으며, 그림에도 나타나듯 NGCF-3이 보다 잘 Grouping하는 것을 확인할 수 있다. Embedding Propagation Layer의 깊이가 Embedding 공간에서 노드를 더 잘 표현하는 것을 의미한다. 별표는 사용자를 의미하고, 원은 아이템을 의미한다.

Conclusion
본 논문에서는 기존의 Embedding 방법과는 달리 Embedding Propagation Layer를 사용하여 Message Construction과 Message Aggregation 과정을 통해 High-order connectivity Graph를 생성하여 제품에 대한 사용자의 선호도를 보다 잘 예측할 수 있는 방안을 제시하였다.
차이나 대학의 NCF를 제안하신 Xiangnan He 교수님이 교신저자로 들어가 있는 논문이며, 추천 시스템에 Graph Mining을 접목시킨 논문 중 재미있는 논문이라 생각이 든다. 다음 논문 리뷰에서는 추천 시스템에서 Graph Mining과 Review까지 고려한 GraphRec과 NGCF의 문제점을 보완한 LightGCN도 리뷰하고자 한다.
Reference
[1] https://www.youtube.com/watch?v=ce0LrvVblCU
[2] http://cinslab.com/wp-content/uploads/2021/05/huangkaiwen-SIGIR-2019-NGCF.pdf