Contents
Graph Neural Networks for Social Recommendation (WWW'19)는 소셜 네트워크에서 추천시스템을 적용한 논문이며, 당시 SoTA 성능에 도달한 GraphRec이다. 현재까지도 사용되는 기법이기도 하고, 이를 기반으로 한 많은 Application 연구도 진행되고 있다.
Abstract
최근 몇 년 동안 Graph Neural Networks (GNNs)은 node information와 위상적인(topological) 구조를 자연스럽게 통합하고 그래프 데이터에서 모델을 학습하는 성능이 우수한 것이 검증되었다. 소셜 네트워크에서는 user-user 혹은 user-item graph 구조를 가지고 있기 때문에 소셜 네트워크에 GNN을 적용할 경우 우수한 성능을 발휘할 수 있다. 따라서, 본 논문에서는 소셜 추천시스템을 위한 Graph neural networks framework (GraphRec)을 제안한다. GraphRec은 user와 item 간의 user-item graph에서 interaction과 opinion을 포착하는 접근법을 제안하며, 두 개의 그래프와 heterogeneous strength을 제대로 모델링할 수 있다.
Introduction
소셜 네트워크는 친구, 동료 등과 같은 주변 사람들을 통해 정보를 획득하고 유포하는 현상(phenomenon)을 기반으로 개발되었으며, user의 사회적 관계가 정보 필터링에 중요한 역할을 한다. 따라서, 사회적 관계를 제대로 파악하는 경우 모델의 추천 성능을 향상시키는데 도움이 된다는 것으로 입증되었다. 최근 연구에 따르면 GNN이 그래프의 topological 구조를 잘 학습할 수 있는 것으로 검증되었다. 그러나 소셜 네트워크와 같은 구조는 아래 그림과 같이 user 간의 관계와 user-item 간의 관계를 다루는 두 가지의 그래프가 결합된 구조를 가지고 있다.

이 구조는 기존의 GNN에서 다루는 그래프 구조와 다르기 때문에 정보를 어떻게 aggregate할지에 대한 문제에 직면하였다. 해당 문제는 다음과 같은 다양한 Challenges가 존재한다. 첫 번째, 정보를 보다 잘 aggregate하기 위해 user-item interaction graph 뿐만 아니라 user opinion graph를 결합하는 것이다. 두 번째, user와 item 간의 interaction과 opinion을 한꺼번에 포착하는 것이다. online에서 user 간의 관계는 서로 다른 관계를 가지고 있을 수 있다. 예를 들어, user가 서로 친한 관계를 띄고 있다면 유사한 취향을 더 많이 공유할 수 있기 때문에 weight를 따로 두지 않고 모델을 학습할 경우 추천 성능이 저하될 수 있다. 따라서, 마지막으로, weight를 고려하는 것이다.
본 논문에서는 위 3 가지 과제를 모두 해결할 수 있는 GraphRec을 제안한다. GraphRec을 통해 다음과 같은 Contribution을 할 수 있다. 첫 번째, 새로운 방법의 Graph Neural Network (GraphRec)을 제안하며 , 이는 소셜 추천시스템에서 일관되게 사용이 가능하다. 두 번째, user-item graph에서 interaction과 opinion을 모두 capture할 수 있는 접근 방식을 제공한다. 세 번째, heterogeneous strength를 수학적으로 고려하는 방법을 소개한다. 마지막으로, 실제 다양한 데이터에서 GraphRec이 효율적인 것을 검증하였다.
The Proposed Framework
Definition and Notation
- $r_{ij}$: The rating value of item $v_j$ by user $u_i$
- $q_j$: The embedding of item $v_j$
- $p_i$: The embedding of user $u_i$
- $e_r$: The opinion embedding for the rating levbel $r$, such as 5-star rating, $r \in \{1, 2, 3, 4, 5\}$
- $d$: The length of embedding vector
- $C(i)$: The set of items which user $u_i$, interacted with
- $N(i)$: The set of social friends who user $u_i$, directly connected with
- $B(j)$: The set of users who have interacted the item $v_j$
- $\boldsymbol{h}^I_i$: The item-space user latent factor from item set $C(i)$ of user $u_i$
- $\boldsymbol{h}^S_i$: The social-space user latent factor from the social friends $N(i)$ of user $u_i$
- $\boldsymbol{h}_i$: The user latent factor of user $u_i$, combining from item space $\boldsymbol{h}^I_i$ and social space $\boldsymbol{h}^S_i$
- $\boldsymbol{x}_{ia}$: The opinion-aware interaction representation of item $v_a$ for user $u_i$
- $\boldsymbol{f}_{jt}$: The opinion-aware interaction representation of user $u_t$ for item $v_j$
- $\boldsymbol{z}_j$ : The item latent factor of item $v_j$
- $\alpha_{ia}$: The item attention of item $v_a$ in contributing to $\boldsymbol{h}^I_i$
- $\beta_{io}$: The social attention of neighboring user $u_o$ in contributing to $\boldsymbol{h}^S_i$
- $\mu_{jt}$: The user attention of user $u_t$ in contributing to $z_j$
- $r^\prime_{jt}$: The predicted rating value of item $v_j$ by user $u_i$
- $\oplus$: The concatenation operaor of two vectors
- $T$: The user-user social graph
- $\boldsymbol{R}$: The user-item rating matrix (user-item graph)
- $\boldsymbol{W}, \boldsymbol{b}$: The weight and bias in neural network
user 집합과 item 집합을 각각 $U = \{u_1, u_2, ..., u_n\} \ \text{and} \ V = \{v_1, v_2, ..., v_m\} $이라고 하자. $n$은 user의 수를 의미하고, $m$은 item의 수를 의미한다. 이때 user-item rating matrix $\boldsymbol{R}^{n \times m}$이 된다. 만약 user $i$가 item $j$에 rating을 부여한 경우 $r^\prime_{ij}$는 1에서 5 사이의 값이 표기되고, rating을 부여하지 않은 경우 $r^\prime_{ij}$ = 0으로 표기된다. 이는 $\mathcal{O} = \{ \left\langle u_i, v_j \right\rangle | r_{ij} \neq 0 \}$, $\mathcal{T} = \{ \left\langle u_i, v_j \right\rangle | r_{ij} = 0 \} $로 표현할 수 있다.
An Overview of the Proposed Framework
본 논문에서 제안하는 GraphRec의 구조는 아래의 그림과 같다. GraphRec은 user modeling, item modeling, rating prediction 총 3 가지 요소로 구성되어 있다. 먼저, user modeling은 user의 latent factor를 학습한다. 소셜 네트워크의 데이터는 social graph와 user-item graph로 구성되어 있기 때문에, 각각 나누어서 서로 다른 관점으로부터 user representation을 학습하는 방법을 제공한다. 하나는 item aggregation이며, 이는 user-item graph에서 user와 item 간의 interaction을 통해서 사용자를 이해하는 aggregation이다. 나머지 하나는 social aggregation이며, 이는 social graph에서 social-space로 부터 user 간의 관계를 파악하는 aggregation이다. 최종적으로 item-space, social-space로 부터 정보를 결합함으로써 user latent factor를 얻을 수 있다.
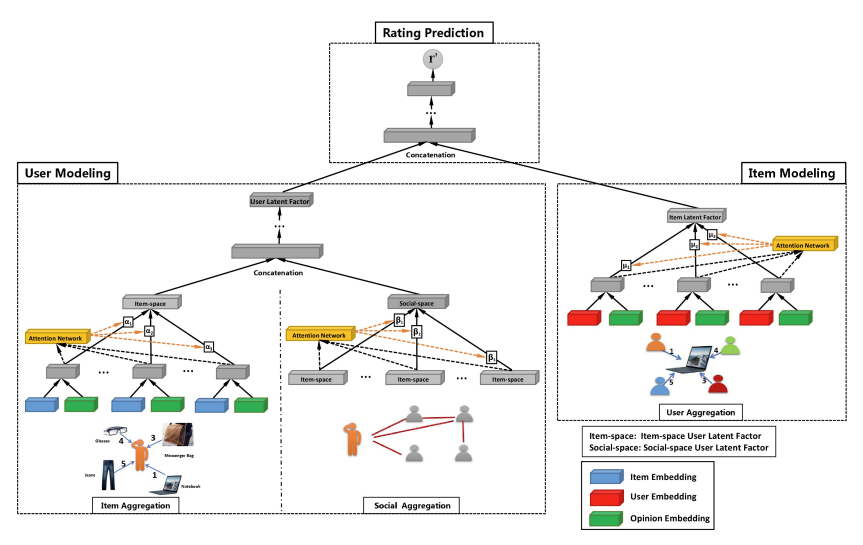
item modeling은 item의 latent factor를 학습하는 것이다. user-item graph에서 interaction과 opinion을 각각 고려하기 위해 user aggregation을 사용한다. user aggregation은 user의 item에 대한 opinion을 aggregate한다. 마지막으로 rating prediction은 user modeling과 item modeling을 통합하고 prediction하면서 model parameter를 학습한다.
User Modeling
위에서 언급한 내용처럼 user modeling은 user latent factor $\boldsymbol{h}_i \in \mathbb{R}^d$를 학습하는 것에 초점을 둔다. 이때 핵심 Challenge는 user-item graph와 social graph를 어떻게 결합하는 것인지에 대한 부분이다. 해당 문제를 해결하기 위해 item aggregation과 social aggregation를 이용한다. item aggregation은 user-item graph로 부터 item-space user latent factor $\boldsymbol{h}^I_i \in \mathbb{R}^d $를 학습하는 것이며, social aggregation은 social graph로 부터 social-space user latent factor $\boldsymbol{h}^S_i \in \mathbb{R}^d$를 학습하는 것이다. 최종적으로는 둘을 결합하여 최종 user latent factor $\boldsymbol{h}_i$를 도출한다.
Item Aggregation
user-item graph는 user와 item 간의 interaction 뿐만 아니라 user가 남긴 item에 대한 opinion(or rating score)도 포함되어 있다. 따라서, 본 논문에서는 item-space user latent factor $\boldsymbol{h}^I_i$를 학습하기 위한 interaction과 opinion을 동시에 capture할 수 있는 접근법을 제공한다. item aggregation은 user $u_i$와 interaction이 존재하고, user의 opinion이 존재하는 item을 고려하면서 item-space user latent factor $\boldsymbol{h}^I_i$를 학습하는 것이 목적이다. 이를 수식으로 표현하면 다음과 같다.
\[ \boldsymbol{h}^I_i = \sigma ( \boldsymbol{W} \cdot \text{Aggre}_{\text{items}} ( \{ \boldsymbol{x}_{ia}, \forall a \in C(i)) \} ) + \boldsymbol{b} ) \]
$\text{Aggre}_{\text{item}}$은 Aggregation function을 의미하고, $\sigma$는 non-linear function 중 ReLU를 의미하며, 나머지 notation은 위에서 언급한 notation과 동일하다. 이때 $\boldsymbol{x}_{ia}$는 MLP를 통한 item emedding $\boldsymbol{q}_a$와 opinion embedding $\boldsymbol{e}_r$의 combination을 의미하며, 아래와 같은 수식으로 계산된다.
\[ \boldsymbol{x}_{ia} = g_v ( [ \boldsymbol{q}_a \oplus \boldsymbol{e}_r ] ) \]
$g_v$는 $\boldsymbol{q}_a$와 $\boldsymbol{e}_r$을 융합하는 것을 의미하며, MLP를 사용한다. $\text{Aggre}_{\text{items}}$로 주로 사용되는 함수는 mean으로 본 논문에서는 $\{ \boldsymbol{x}_{ia}, \forall a \in C (i) \}$에 대해서 element-wise mean를 적용하였다. localized spectral convolution의 mean aggregator는 아래와 같은 수식을 따른다.
\[ \boldsymbol{h}^I_i = \sigma( \boldsymbol{W} \cdot \left\{ \sum_{a \in C(i)} \alpha_i \boldsymbol{x}_{ia} \right\} + \boldsymbol{b} ) \]
$\alpha_i$는 $\frac{1}{|C(i)|}$를 의미한다. 모든 값을 더한 후 item의 수 만큼 나누어주는 것이다. 이와 같은 방식은 user마다 interaction의 영향이 서로 다를 수 있기 때문에 최적화하는 방식이 아닐 수 있다. 따라서, 각 interaction에 가중치를 할당해서 item에 따라 서로 다른 contribution을 줄 수 있도록 Attention mechanisms을 사용하여 아래와 같이 설정한다.
\[ \boldsymbol{h}^I_i = \sigma( \boldsymbol{W} \cdot \left\{ \sum_{a \in C(i)} \alpha_{ia} \boldsymbol{x}_{ia} \right\} + \boldsymbol{b} ) \]
이를 통해 $(v_a, u_i)$ 각각의 pair에 대해서 개별적인 weight를 할당할 수 있다. 이는 2-layer 구조를 가지는 attention network로 $\alpha_{ia}$를 학습할 수 있으며 수식은 아래와 같이 표현된다.
\[ \alpha^*_{ia} = w^T_2 \cdot \sigma(\boldsymbol{W}_1 [ \boldsymbol{x}_{ia} \oplus \boldsymbol{p}_i ] + \boldsymbol{b}_1 ) + b_2 \]
\[ \alpha_{ia} = \frac{\text{exp} ( \alpha^*_{ia} ) }{ \sum_{a \in C(i)} \text{exp}(\alpha^*_{ia}) } \]
Social Aggregation
social correlation theories 때문에 user의 선호도는 user와 직접 연결된 친구들과 유사하거나 영향을 받는다. 따라서, user 간의 유대는 user의 행동에 더 영향을 미칠 수 있다. 다시 말해, social-space latent factor를 학습하는 것은 user의 유대 강도를 고려하여야 한다. 본 논문에서는 이를 고려한 수식을 아래와 같이 제시한다.
\[ \boldsymbol{h}^S_i = \sigma ( \boldsymbol{W} \cdot \text{Aggre}_{\text{neighbors}} ( \{ \boldsymbol{h}^I_o, \forall o \in N(i) \} ) + \boldsymbol{b} ) \]
$\text{Aggre}_{\text{neighbors}}$는 user의 이웃에 대한 aggregation 함수를 의미한다. aggregation 함수로는 mean 함수가 제일 많이 사용되며 이를 수식으로 표현하면 아래와 같다.
\[ \boldsymbol{h}^S_i = \sigma ( \boldsymbol{W} \cdot \left\{ \sum_{o \in N(i)} \beta_i \boldsymbol{h}^I_o \right\} + \boldsymbol{b} ) \]
이때 mean 함수를 사용하기 때문에 $\beta_i = \frac{1}{|N(i)|}$가 된다. 그러나 mean 함수를 사용하게 되면 user 간의 유대 강도를 제대로 고려할 수 없다. 따라서, item aggregation에서도 다룬 attention mechanism을 사용하여 아래와 같은 수식으로 사용한다.
\[ \begin{equation} \begin{split} \boldsymbol{h}^S_i & = \sigma( \boldsymbol{W} \cdot \left\{ \sum_{o \in N(i)} \beta_{io} \boldsymbol{h}^I_o \right\} + \boldsymbol{b} ) \\ \\ \beta^*_{io} & = w^T_2 \cdot \sigma ( \boldsymbol{W}_1 \cdot [ \boldsymbol{h}^I_o \oplus \boldsymbol{p}_i ] + \boldsymbol{b}_1 ) + b_2 \\ \\ \beta_{io} & = \frac{\text{exp}(\beta^*_{io}) }{ \sum_{o \in N(i)} \text{exp}(\beta^*_{io} )} \end{split} \end{equation} \]
Learning User Latent Factor
social graph와 user-item interaction은 서로 다른 정보를 제공하기 때문에 이를 고려하여 user latent factor를 학습하기 위해 item-space user latent factor와 social-space user latent factor를 함께 사용한다. 두 정보를 학습하기 위해서 본 논문에서는 MLP를 사용하여 $\boldsymbol{h}^I_i$와 $\boldsymbol{h}^S_i$를 결합해 최종 $\boldsymbol{h}_i$를 도출한다.
\[ \begin{equation} \begin{split} c_1 & = [ \boldsymbol{h}^I_i \oplus \boldsymbol{h}^S_i ] \\ \\ c_2 & = \sigma(\boldsymbol{W}_2 \cdot c_1 + \boldsymbol{b}_2 ) \\ \\ & \cdots \\ \boldsymbol{h}_i & = \sigma ( \boldsymbol{W}_l \cdot c_{l-1} + \boldsymbol{b}_l ) \end{split} \end{equation} \]
$l$은 hidden layer의 수를 의미한다.
Item Modeling
Item modeling은 item latent factor를 학습하기 위해 사용되며 $\boldsymbol{z}_j$로 표기한다. item은 interaction과 opinion으로 구성되어 있다. 따라서, user modeling에서 한 것과 마찬가지로 이를 모두 고려하여 item latent factor를 잘 학습하여야 한다.
같은 item이라고 하더라도 user마다 opinion이 다를 수 있다. 다양한 user가 제공하는 opinion을 통해 동일한 item의 특성을 잘 파악할 수 있으며, 이는 modeling하는 것에 있어 도움을 준다. 따라서, item에 opinion을 남긴 user의 representation $\boldsymbol{f}_{jt}$을 학습하기 위해 아래와 같은 수식을 따른다.
\[ \boldsymbol{f}_{jt} = g_u ( [ \boldsymbol{p}_t \oplus \boldsymbol{e}_r ] ) \]
$g_u$는 $\boldsymbol{p}_t$와 $\boldsymbol{e}_r$을 융합하는 것을 의미하며, user modeling과 마찬가지로 MLP를 사용한다. 그 후 user representation을 aggregate하는 함수는 아래와 같이 정의할 수 있다.
\[ \boldsymbol{z}_j = \sigma ( \boldsymbol{W} \cdot \text{Aggre}_{\text{users}} ( \{ \boldsymbol{f}_{jt}, \forall t \in B(j) \} ) + \boldsymbol{b} ) \]
여기서도 마찬가지로 attention mechanism을 사용하기 때문에 아래와 같이 표현할 수 있다.
\[ \begin{equation} \begin{split} \boldsymbol{z}_j & = \sigma( \boldsymbol{W} \cdot \left\{ \sum_{t \in B(j)} \mu_{jt} \boldsymbol{f}_{jt} \right\} + \boldsymbol{b} ) \\ \\ \mu^*_{jt} & = w^T_2 \cdot \sigma ( \boldsymbol{W}_1 \cdot [ \boldsymbol{f}_jt \oplus \boldsymbol{q}_j ] + \boldsymbol{b}_1) + b_2 \\ \\ \mu_{jt} & = \frac{ \text{exp} ( \mu^*_{jt} ) }{\sum_{t \in B(j)} \text{exp}(\mu^*_{jt}) } \end{split} \end{equation} \]
Rating Prediction
rating prediction은 model parameter를 학습하는 것에 대해서 다룬다. 본 연구에서는 rating prediction을 위한 GraphRec을 제안하였으며, user와 item에 대한 latent factor를 먼저 연결(concatenate)한 후 MLP를 통과하여 rating을 예측한다.
\[ \begin{equation} \begin{split} \boldsymbol{g}_1 & = [ \boldsymbol{h}_i \oplus \boldsymbol{z}_j ] \\ \\ \boldsymbol{g_2} & = \sigma(\boldsymbol{W}_2 \cdot \boldsymbol{g_1} + \boldsymbol{b}_2 ) \\ \\ & \cdots \\ \\ \boldsymbol{g}_{l-1} & = \sigma ( \boldsymbol{W}_l \cdot \boldsymbol{g}_{l-1} + \boldsymbol{b}_l ) \\ \\ r^\prime_{ij} & = w^T \cdot \boldsymbol{g}_{l-1} \end{split} \end{equation} \]
$r^\prime$은 $u_i$의 $v_j$에 대한 predicted rating을 의미한다.
Model Training
GraphRec의 model parameter를 추정하기 위해서는 optimizer를 설정하여야 한다. 본 논문에서는 목적함수를 아래와 같이 설정하였다.
\[ \text{Loss} = \frac{1}{2|\mathcal{O}|} \sum_{i, j \in \mathcal{O}} (r^\prime_{ij} - r_{ij} )^2 \]
실제 구현 단계에서는 RMSprop을 사용하여 최적화 하였다. 또한, 과적합(Overfitting)을 방지하기 위해 dropout을 사용하였다.
Experiment
본 논문에서는 PMF, SoRec, SoReg, SocialMF, TrustMF, NeuMF, DeepSoR, GCMC+SN 등의 기존 연구에서 성능이 우수하다고 알려진 추천시스템 기법을 활용하여 벤치마크 모델로 사용하였다. 데이터는 Ciao와 Epinion 데이터를 사용하였으며,데이터의 기초 통계와 실험 결과는 다음과 같다.
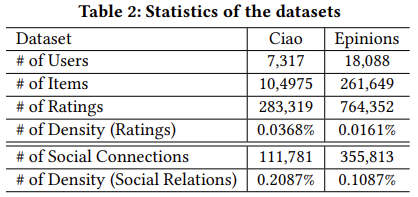

실험 결과, social network information이 추천시스템에 도움을 주는 것을 확인할 수 있으며, neural network를 사용할 경우 추천 성능을 높일 수 있는 것을 확인하였다. 마지막으로, 본 논문에서 제안하는 GraphRec이 다른 기법에 비해 우수한 성능을 발휘하는 것을 확인하였다.
본 논문에서는 GraphRec의 어떤 부분이 추천 성능에 기여하는지를 확인하기 위해 GraphRec의 hyper parameter를 조정하며 GraphRec-SN, GraphRec-Opinion, GraphRec-$\alpha$, GraphRec-$\beta$, GraphRec-$\alpha$&$\beta$, GraphRec-$\mu$ 등 다양한 실험을 진행하였다. GraphRec-SN은 social network information을 지운 버전을 의미하며, GraphRec-Opinion은 $\boldsymbol{x}_{ia}$와 $\boldsymbol{f}_{jt}$를 학습하는 동안 opinion 정보를 지운 버전을 의미한다. 다음으로 $\alpha, \beta$등의 모델은 attetnion mechanism에서 attention을 사용하지 않고 mean aggregate를 사용한 버전을 의미한다.

social information과 opinion을 제거한 경우 기존의 모델에 비해 예측 성능이 저하되는 것을 확인할 수 있으며, attention mechanism을 사용한 경우 성능이 가장 우수한 것을 확인할 수 있다. 마지막 그림인 Figure 5는 embedding size를 달리했을 때의 실험 결과를 의미한다. emedding size가 64인 경우 가장 우수한 성능을 보이는 것을 확인할 수 있다.
Conclusion and Future Work
본 논문에서는 소셜 네트워크 분야에 적용할 수 있는 rating 예측을 위한 GraphRec을 제안해 user-item graph에서 interaction과 opinion을 동시에 포착할 수 있는 접근법을 제공하였다. 본 논문의 실험은 opinion information이 모델의 성능 향상에 있어 중요한 역할을 한다는 것을 확인하였다. 게다가, attention mechanism을 통해 서로 다른 weight를 부여할 경우 성능이 향상되는 것도 확인하였다. 본 연구에서는 정적 데이터를 기반으로 모델을 학습하였으나 실제 소셜 네트워크는 정적 네트워크인 경우가 많다. 따라서, 추후 동적 네트워크에서도 적용할 수 있는 모델을 구축하고자 한다.