Contents
SIGIR'20 에 발표된 LightGCN: Simplifying and Powering Graph Convolution Network for Recommendation을 리뷰하고자 한다. LightGCN은 간단하면서도 강력한 Graph Convolution Network 이다. 기존의 GCN 즉, Spectral GCN은 Node Classification을 하기 위해 만들어졌기 때문에 사용자와 제품 간의 연결성만 다루는 CF 구조에서는 적절하지 않기 때문에, 추천 시스템에 적용하기 위해 LightGCN을 제안하였다.
Abstract
본 논문이 발표되기 전에는 GCN (Graph Convolution Network) 를 기반으로 추천 시스템을 구축하였다. GCN은 graph mining을 하기 위해 제안된 모델이기에 구조상 적합하지 않았다. GCN에 design한 feature transformation과 nonlinear activation는 학습에 거의 도움이 되지 않았으며, 심지어 이를 추가할 경우 오히려 학습이 어려워지고 추천 성능이 감소한다는 문제점이 존재했다.
본 연구에서는 이러한 GCN 구조를 "neighborhood aggregation"라는 필수 요소만을 고려한 형태로 간결하게 변경하여 추천 성능을 개선 시킨 LightGCN을 제안하였다. LightGCN은 users embedding과 item embedding을 학습시키고 모든 레이어를 거쳐 산출된 weight sum을 최종 embedding으로 사용하였다. 이처럼 간단한 구조를 보이고 있으나 NGCF (Neural Graph Collaborative Filtering)보다 16% 우수한 성능을 발휘하였다.
[Tensorflow Code] [Pytorch Code] [Original Paper]
Introduction
NGCF는 high-hop neighhors로 sub-graph 구조의 사용을 심화한 모델이며, 이는 GCN으로 부터 발전된 모델이다. NGCF는 GCN의 구조를 기반으로 feature transformation, neighborhood aggregation과 nonlinear activation을 통해 user, item embedding을 구체화 하였으나 이러한 구조는 매우 무겁고 burdensome하였다. 본 논문에서는 이러한 문제점을 극복한 LightGCN을 제안하였으며, NGCF와 LightGCN을 비교한 결과는 다음과 같다. (hop은 network 구조에서 출발지와 목적지 사이에 위치한 경로의 한 부분을 의미하며, Graph에서 high-hop은 target node에서 얼마만큼 떨어져 있는지를 의미한다.)
NGCF
NGCF는 feature transformation, neighborhood aggregation 그리고 nonlinear activation을 propagation rule을 통해 embedding을 구체화하고 있다. 본 논문에서는 실험을 통해 faeture transformation과 nonlinear activation은 오히려 학습에 방해된다는 사실을 발견하였다. semi-supervised node classification에서는 각 노드에 다양한 semantic feature가 존재한다. 그렇기에 nonlinear transformation이 feature의 학습에 긍정적인 영향을 제공하였다. 그러나 Collaborative Filtering의 input은 단순히 user-item interaction만을 고려하기 때문에 sematic한 정보가 없어서 오히려 성능을 저하한다.
LightGCN은 학습에 도움되지 않는 nonlinear activation과 feature transformation을 제거하고 neighborhood aggregation만을 weighted sum하여 embedding을 구체화함으로써 모델의 구조를 간단하게 만들고 성능을 개선시켰다. LightGCN의 구조를 살펴보기 이전 NGCF의 구조를 먼저 살펴보자. NGCF에서는 user-teim interaction graph를 활용하여 다음과 같이 embedding을 전파한다.
\[ \boldsymbol{e}^{(k+1)}_u = \sigma (\boldsymbol{W}_1 \boldsymbol{e}^{(k)}_u + \sum_{i \in N_u} \frac{1}{\sqrt{|N_u||N_i|}} (\boldsymbol{W}_1 \boldsymbol{e}^{(k)}_i + \boldsymbol{W}_2 (\boldsymbol{e}^{(k)}_i \odot \boldsymbol{e}^{(k)}_u ))) \]
\[ \boldsymbol{e}^{(k+1)}_i = \sigma (\boldsymbol{W}_1 \boldsymbol{e}^{(k)}_i + \sum_{u \in N_i} \frac{1}{\sqrt{|N_u||N_i|}} (\boldsymbol{W}_1 \boldsymbol{e}^{(k)}_u + \boldsymbol{W}_2 ( e^{(k)}_u \odot \boldsymbol{e}^{(k)}_i ))) \]
$\boldsymbol{e}^{(k)}_u$와 $\boldsymbol{e}^{(k)}_i$는 각각 k-layer 만큼 propagation된 embedding을 의미한다. $\sigma$는 nonlinear activation function을 의미하고, $N_u$는 user $u$와 interaction이 존재하는 item $i$의 집합을 의미하며 $N_i$는 item $i$와 interaction이 존재하는 user $u$의 집합을 의미한다. 마지막으로, $\boldsymbol{W}_1$과 $\boldsymbol{W}_2$는 feature transformation metrices를 의미한다. 만약 3-hop neighbors를 설정한다면 아래와 같은 그림으로 표현할 수 있다.
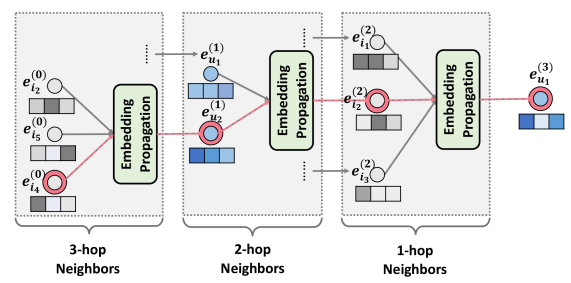
LightGCN
LightGCN arthitecture
기존에 제안된 GCN 기반 모델의 Aggregator의 경우 feature transformation과 nonlinear function을 사용하고 있다. 그러나 이와 같은 함수는 CF 기법에서는 성능이 좋지 않다. 따라서, LightGCN은 추천을 위한 GCN의 필수적인 성분(ingredient)만을 사용하여 NGCF를 경량화하고 성능을 개선하기 위해 제안된 모델이다. GCN의 기본적인 아이디어는 Graph에 대한 smoothing feature를 통해 node에 대한 representation을 학습하는 것이며, 이를 위해 Graph Convolution을 반복적으로 수행한다(image classification에서 conv-layer를 거쳐가며 보다 복잡한 feature를 추출하는 것과 비슷한 맥락). 이를 수식으로 표현하면 다음과 같다.
\[ \boldsymbol{e}^{(k+1)}_u = \text{AGG}(\boldsymbol{e}^{(k)}_u, {\boldsymbol{e}^{(k)}_i : i \in N_u}) \]
\[ \boldsymbol{e}^{(k+1)}_u = \sum_{i \in N_u} \frac{1}{\sqrt{|N_u|} \sqrt{|N_i|}} \boldsymbol{e}^{(k)}_i \]
\[ \boldsymbol{e}^{(k+1)}_i = \sum_{u \in N_i} \frac{1}{\sqrt{|N_i|} \sqrt{|N_u|}} \boldsymbol{e}^{(k)}_u \]
$\frac{1}{\sqrt{|N_u|} \sqrt{|N_i|}}$는 standard GCN[paper]의 symmetric normalization term을 의미하며, normalization term을 수행하는 이유는 convolution operation을 통한 embedding scale의 증가를 피하기 위함이다. L1 norm과 같은 다른 normalization 기법도 존재하지만 symmetric normalization이 가장 우수한 성능을 발휘하여 본 논문에서는 이를 통해 학습을 진행한다.
LightGCN은 기존에 제안된 Graph convolution operations과는 달리 연결된 neighbors에 대해서만 계산했기 때문에(아래의 NGCF에서는 target node $e^{(l-1)}_{u_1}$가 같이 연산하고 있음. 이를 self-connection이라 부름) self-connection이 필요없다.


Layer Combination and Model Prediction
LightGCN은 오직 첫 번째 Layer인 $e^{(0)}_u$와 $e^{(0)}_i$ 만 학습이 가능하다. 첫 번째 Layer를 제외한 나머지 Layer는 propagation rule에 의해 전파되어 학습이 필요없기 때문이다. 그 후 최종 representation을 위해 각 layer를 결합(conbine)하며, 이때의 수식은 다음과 같다.
\[ \boldsymbol{e}_u = \sum^{K}_{k=0} \alpha_k \boldsymbol{e}^{(k)}_u;\ \ \ \boldsymbol{e}_i = \sum^{K}_{k=0} \alpha_k \boldsymbol{e}^{(k)}_i \]
$\alpha_k$는 k번째 layer embedding의 중요도를 의미한다. 이는 최적화해야 될 hyper parameter 혹은 model parameter를 의미한다. 원래는 학습을 통해 최적의 $\alpha_k$를 찾는 것이 우수한 성능을 나타낼 수 있지만, 저자는 논문이 복잡해지는 것을 피하기 위해 $\alpha_k$를 simple하게 $\frac{1}{(K+1)}$로 설정했다.
본 논문에서는 layer를 모두 combine하여 최종 representation을 얻는데, 이러한 구성을 수행하는 이유는 다음과 같다.
- layer의 수가 증가함에 따라 마지막 layer의 embedding이 over-smoothed 되기 때문에, 마지막 layer만을 사용하는 것은 문제가 존재한다.
- 각각의 layer에서 서로 다른 semantic을 포착한다. 따라서, 서로 다른 정보를 포착한 결과를 결합함으로써 보다 포괄적인(comprehensive) representation을 추출할 수 있다.
- 서로 다른 layer의 embedding을 가중합(weighted sum)을 통해 결합함으로써 기존의 Graph Convolution이 가진 self-connected의 효과를 포착할 수 있다.
가중합을 통해 계산된 $\boldsymbol{e}_u$와 $\boldsymbol{e}_i$는 최종적으로 inner product를 통해 $\hat{y}_{ui}$를 출력한다. ($\hat{y}_{ui} = \boldsymbol{e}^T_u \boldsymbol{e}_{i}$)
Matrix Form
LightGCN의 embedding 방식을 계산하기 위해 Matrix Form을 설명하면 다음과 같다. user-item interaction matrix를 $\boldsymbol{R} \in \mathbb{R}^{M \times N}$으로 표현할 수 있으며, 이때 $M$과 $N$은 각각 user의 수, item의 수를 의미한다. 이때, user-item graph의 adjacency matrix $\boldsymbol{A}$는 다음과 같이 표현할 수 있다.
\[ \boldsymbol{A} = \begin{pmatrix} \boldsymbol{0} & \boldsymbol{R} \\ \boldsymbol{R}^T & \boldsymbol{0} \end{pmatrix} \]
이때, 0 번째 layer의 embedding matrix를 $\boldsymbol{E}^{(0)} \in \mathbb{R}^{(M \times N) \times T}$로 표현할 수 있으며, $T$는 embedding size를 의미한다. 이와 같은 방식으로 $\boldsymbol{E}^{(k+1)}$를 표현하면 수식은 다음과 같다.
\[ \boldsymbol{E}^{(k+1)} = (\boldsymbol{D}^{-\frac{1}{2}} \boldsymbol{A} \boldsymbol{D}^{\frac{1}{2}} ) \boldsymbol{E}^{(k)} \]
$\boldsymbol{D}$는 $(M + N) \times (M + N)$ 차원을 가진 diagonal matrix(Degree matrix라고도 부름)를 의미한다. diagonal matrix는 대각 성분을 제외한 나머지 index는 전부 0의 값을 가진 matrix를 의미한다. $D_{ii}$는 adjacency matrix $\boldsymbol{A}$의 차수(Degree)를 의미한다. 이에 관련된 내용은 여기를 참고하면 보다 상세히 작성해두었다.
위에서 언급 했듯 k 번째 layer의 가중치는 $\alpha_k$로 표현한다고 언급했다. 이를 통해 $\boldsymbol{E}$를 표현하면 수식은 다음과 같이 나타낼 수 있다.
\[ \begin{equation} \begin{split} \boldsymbol{E} & = \alpha_0 \boldsymbol{E}^{(0)} + \alpha_1 \boldsymbol{E}^{(1)} + \cdots + \alpha_K \boldsymbol{E}^{(K)} \\ \\ & = \alpha_0 \boldsymbol{E}^{(0)} + \alpha_1 \tilde{\boldsymbol{A}} \boldsymbol{E}^{(0)} + \cdots + \alpha_K \tilde{\boldsymbol{A}}^{K} \boldsymbol{E}^{(K)} \end{split} \end{equation} \]
$\tilde{\boldsymbol{A}} = \boldsymbol{D}^{-\frac{1}{2}} \boldsymbol{A} \boldsymbol{D}^{-\frac{1}{2}}$로 symmetrically normalized matrix를 의미한다. propagation rule로 인해 $\boldsymbol{E}^{(0)}$이 고정되어 있고, $\tilde{\boldsymbol{A}}$만 제곱함으로써 계산의 효율성을 증가시켰다.
Model Analysis
본 논문에서는 LightGCN이 단순히 구조를 간단히 한 것 뿐만 아니라는 이면에 존재하는 합리성을 입증하기 위해 다음과 같은 총 3가지 측면을 언급하고 있다.
Connection
본 연구에서는 self-connection을 하지 않더라도 동일한 효과를 발휘한다고 언급하였다. self-connection의 경우 identity matrix ($\boldsymbol{I}$)를 adjacency matrix ($\boldsymbol{A}$)에 더하는 것으로 표현할 수 있으며, 수식은 다음과 같다(이는 Simplified GCN (SGCN)에서 증명함).
\[ \boldsymbol{E}^{(k+1)} = (\boldsymbol{D} + \boldsymbol{I})^{-\frac{1}{2}} (\boldsymbol{A} + \boldsymbol{I})(\boldsymbol{D} + \boldsymbol{I})^{-\frac{1}{2}} \boldsymbol{E}^{(k)} \]
이때 identity matrix는 Diagonal matrix와 동일한 차원을 가진다. 위 수식에서 $(\boldsymbol{D} + \boldsymbol{I})^{-\frac{1}{2}}$는 학습에 사용되지 않고 embedding을 re-scale하는 것에만 관련이 있기에 생략한다. 이후 k 번째 embedding matrix를 구하는 수식은 다음과 같이 표현할 수 있으며, LightGCN에서 가중합한 식과 동일하게 된다.
\[ \begin{equation} \begin{split} \boldsymbol{E}^{(k)} & = (\boldsymbol{A} + \boldsymbol{I} \boldsymbol{E}^{(K-1)} = (\boldsymbol{A} + \boldsymbol{I})^K \boldsymbol{E}^{(0)} \\ \\ & = \begin{pmatrix} K \\ 0 \end{pmatrix} \boldsymbol{E}^{(0)} + \begin{pmatrix} K \\ 1\end{pmatrix} \boldsymbol{AE}^{(0)} + \cdots + \begin{pmatrix} K \\ K \end{pmatrix} \boldsymbol{A}^K \boldsymbol{E}^{(0)} \end{split} \end{equation} \]
위 수식은 이항정리를 통해 계산할 수 있는 수식이다.
Over-smoothing
LightGCN은 마지막 Layer로 인한 Over-smoothed를 막기 위해 weighted sum을 사용하였다. Over-smoothing은 Layer의 수가 증가하면 증가할수록 node의 embedding이 서로 유사해지는 현상을 의미한다. node 간의 거리가 너무 가까운데에서 발생하는 문제이며, over-smoothing 추천 성능을 저하시킨다. 이를 극복하기 위해 $\boldsymbol{E}^{(k)}$를 구할 때 initial embedding을 더해 줌으로써 over-smoothing을 해결하고, 이를 수식으로 나타내면 다음과 같다.
\[ \boldsymbol{E}^{(k+1)} = \beta \boldsymbol{E}^{(0)} + (1 - \beta) \tilde{\boldsymbol{A}} \boldsymbol{E}^{(k)} \]
이때 $\beta$를 통해 initial embedding의 영향력을 제어할 수 있다.
Second-Order Embedding Smoothness
LightGCN은 nonlinear activation을 사용하지 않는다. 즉, 간단하고 linear하기 때문에 smooth embedding으로 부터 더 많은 인사이트를 얻을 수 있다. 이를 아래와 같이 표현함으로써 user와 user 간의 공통으로 연결된 item으로 부터 smoothness의 강도를 나타내는 coefficient를 구할 수 있다.
\[ \boldsymbol{e}^{(2)}_u = \sum_{i \in N_u} \frac{1}{ \sqrt{|N_u|} \sqrt{|N_i|} } \boldsymbol{e}^{(1)}_i = \sum_{i \in N_u} \frac{1}{|N_i|} \sum_{v \in N_i} \frac{1}{ \sqrt{|N_u|} \sqrt{|N_v|} } \boldsymbol{e}^{(0)}_v \]
\[ c_{v \rightarrow u} = \frac{1}{\sqrt{|N_u|} \sqrt{|N_v|}} \sum_{i \in N_u \cap N_v } \frac{1}{|N_i|} \]
interaction이 많은 item의 수가 많을수록 coefficient는 커지고, user $u$와 연결된 $v$가 적을수록 coefficient가 커지는 것을 확인할 수 있다.
Model Training
LightGCN에서 학습해야 할 parameter는 첫 번째 layer의 embedding 뿐이며, 이는 $\theta = \boldsymbol{E}^{(0)}$를 의미한다. 다시 말하자면, 모델의 복잡성(Complexity)는 Matrix Factorization (MF)와 동일하다. 본 논문에서는 Bayesian Personalized Ranking (BPR) loss를 사용하여 모델을 최적화 하였다. BPR는 실제 구매한 item과 구매하지 않은 item의 차이를 계산하여 실제 구매한 item에는 높은 가중치를 부여하고, 구매하지 않은 item에는 낮은 가중치를 부여하는 방식이며, 수식은 다음과 같다.
\[ \text{L}_{\text{BPR}} = -\sum^M_{u=1} \sum_{i \in N_u} \sum_{j \notin N_u} \ln \sigma(\hat{y}_{ui} - \hat{y}_{uj}) + \lambda ||\boldsymbol{E}^{(0)} || ^2 \]
$M$은 user의 수를 의미하고, $i$는 구매한 item의 집합을, $j$는 구매하지 않은 item의 집합을 의미한다. $\hat{y}_{ui}$와 $\hat{y}_{uj}$는 각각 user $u$가 item $i$를 구매할 확률과 item $j$를 구매하지 않을 확률을 의미한다. $\lambda$는 L2-norm을 의미한다.
Experiments
본 논문에서는 Gowalla, Amazon-Book과 Yelp2018 데이터를 사용하여 LightGCN과 NGCF를 비교하였다. Yelp2018의 경우 데이터가 변경되어 새로 실험을 진행한 후 결과를 비교하였다.


성능을 보면 LightGCN이 NGCF보다 전체적으로 우수한 성능을 발휘하고 있는 것을 확인할 수 있다. loss를 보면 LightGCN이 보다 빨리 수렴하는 것을 확인할 수 잇다. NGCF에 비해 속도 면에서도 우수하고, 성능 면에서도 우수한 것이다.

LightGCN-single은 각 layer를 combination을 하지 않은 후 학습을 진행한 결과를 의미하고, LightGCN은 layer combination을 수행한 결과를 의미한다. LightGCN의 경우 Layer의 수가 증가함에 따라 데이터셋에 상관없이 성능이 개선되는 것을 확인할 수 있으나, LightGCN-single의 경우 일부 데이터에 대해서는 LightGCN에 비해 우수한 성능을 보이고 있으나, Layer가 증가함에 따라 성능이 감소하는 추세를 보이고 있다. 이는 over-smoothing 문제가 발생한 것을 의미한다.
Conclusion
본 연구에서는 feature Transformation과 nonlinear activation이 오히려 학습에 방해가 되고, 성능이 저하된다는 사실을 확인하였다. 또한, weighted sum이 self-connection의 효과를 나타내어 over-smoothing 문제를 일부 제어하는데 도움이 되는 사실도 확인하였다.
'Paper review > Recommender System' 카테고리의 다른 글
| Graph Neural Networks for Social Recommendation (WWW'19) (0) | 2022.08.01 |
|---|---|
| Neural Graph Collaborative Filtering (SIGIR'19) (0) | 2022.06.12 |
| Collaborative Filtering for Implicit Feedback Datasets (ICDM'08) (0) | 2022.03.17 |
| AutoRec: Autoencoders Meet Collaborative Filtering (WWW'15) (0) | 2022.03.09 |
| [Short] Sentiment Analysis in TripAdvisor, Ana Valdivia (2017) (0) | 2021.11.06 |