본 논문에서는 Autoencoder에 기반한 새로운 CF 모델인 AutoRec을 제안하였다. AutoRec은 기존의 Neural Network 에 비해 representational 하고 computational advantages가 있다고 주장하며, 현재의 SOTA(State-of-the-Art) 성능에 도달하는 것을 입증했다. 그럼 이제 AutoRec이 어떤 모델인지 살펴보자.
AutoRec Model
평점 기반 CF(Collaborative Filtering)에서는 사용자의 수는 $m$, 아이템의 수는 $n$이라고 설정할 경우 사용자-아이템 간 상호작용을 표현하는 평점 행렬 $R$은 $R \in \mathbb{R}^{m \times n}$가 되며, 사용자 $u$는 $u \in U = \{1,...,m\}$로, 아이템 $i$는 $i \in I = \{1, ..., n\}$가 된다. $U$와 $I$는 각각 사용자 집합, 아이템 집합을 의미한다. 또한, 각 아이템에 대한 평점 vector는 다음과 같이 정의할 수 있다.
\[ r^{(i)} = (R_{1i}, ..., R_{mi}) \in \mathbb{R}^m \]
$r^{(i)}$는 사용자가 아이템 $i$에 대해 측정한 평점들의 vector를 의미한다. 이와 같이 변수들을 정의한 이유는 item-based 혹은 user-based autoencoder를 design 하기 위함이었다. 우리는 누락된 평점을 예측하기 위해 관찰된 vector를 입력으로 사용하고, 저차원 공간에 project 시켜 vector를 재구성한다. $\mathbb{R^d}$ 차원에서 vector의 집합 $S$와 $k \in \mathbb{K_+}$가 주어졌다면 autoencoder는 다음과 같이 cost function을 정의할 수 있다($k$는 hidden node의 수).
\[ \min_{\theta} \sum_{r \in S} ||r - h(r;\theta)||^2_2 \]

여기서 +1은 bias를 의미하고, $W, V$는 각각의 node에 모두 연결되어 있다. 위 그림에서 음영처리가 된 부분은 실제 관측된 ratings을 의미하고, $r^{(i)}$를 학습하기 위한 weight의 solid connection을 의미한다. 우리는 위에서 모델을 학습하기 위해 실제 item rating vector $r$과 $h(r;\theta)$의 최소화 하는 $\theta$를 찾는 방향으로 학습한다고 언급했다. $h(r;\theta)$는 모델이 예측한 평점 행렬을 의미하며 다음과 같은 수식으로 표현할 수 있다.
\[ h(r;\theta) = f(W \cdot g(Vr + \mu) + b) \]
$f(\cdot)$과 $g(\cdot)$은 활성화 함수를 의미하며, $\theta = \{W, V, \mu, b \}$ 이다. $V$는 item ratings vector와 hidden node 간을 연결해주는 weight 부분이고, $W$는 hidden node와 다시 출력되는(우리가 생성한) item ratings vector 간을 연결해주는 weight 부분이다. 또한, $\mu$와 $b$는 bias를 의미하고 각각 parameter의 차원은 다음과 같다.
\[ V \in \mathbb{R}^{d \times k}, \ W \in \mathbb{R}^{k \times d}, \ \ \mu \in \mathbb{R}^k, \ \ r \in \mathbb{R}^d, \ \ b \in \mathbb{R}^d \]
cost를 최소화하기 위해서는 backpropagation을 통하여 $\theta$를 학습해야한다는 것은 자명한 사실이다. AutoRec의 cost function은 위에서 다루었던 autoencoder의 cost function과는 약간 다르게 regularization 항이 추가되어 있으며, 다음과 같은 수식으로 표현할 수 있다.
\[ \min_{\theta} \sum^n_{i=1} || r^{(i)} - h(r^{(i)};\theta))||^2_{\mathcal{O}} + \frac{\lambda}{2} \cdot (||W||^2_F + ||V||^2_F ) \]
$||\cdot||^2_{\mathcal{O}}$은 오직 관찰된 평점의 contribution만을 고려한다는 것을 의미한다. $||\cdot||^2_F$는 논문에서 따로 언급은 하지 않았지만, 행렬 크기를 계산할 때 사용하는 Frobenius norm을 의미하는 것으로 유추한다. $r^{(i)}$는 Item-based AutoRec(I-AutoRec)의 ratings vector를 의미하고, User-based AutoRec(U-AutoRec)일 경우 $\{r^{(u)}\}^m_{u=1}$로 표기한다. I-AutoRec의 경우 각 유저에 대해서 값을 계산하기에 I-AutoRec은 총 $2mk + m + k$개의 parameter를 가지며, 사용자 $u$가 아이템 $i$에 측정한 평점의 수식은 다음과 같다.
\[ \hat{R}_{ui} = (h(r^{(i)}; \hat{\theta}))_u \]
본 논문에서는 Restricted Bolzmann Machines based CF(RBM-CF)를 비교 모델로 선정하여 모델을 평가하였다. RBM에 대한 내용은 여기를 참고하면 된다. 본 논문에서는 AutoRec과 RBM-CF 간의 차이점으로 총 네 가지를 언급하였다.
1. purpose
RBM-CF는 확률 밀도 함수(probability density function; pdf)를 모델링하는 것을 목적으로 하는 Generative model이지만, AutoRec은 Discriminative model 기반이다. Discriminative model은 Logistic과 같은 model을 의미하고, Generative model은 Gaussian Mixture Model과 같은 model을 의미한다.
2. cost function
RBM-CF의 경우 pdf를 모델링하는 것이 purpose이므로 확률이 최대가 되는 값을 산출하기 위해 MLE(Maxtimum Likelihood Estimate)를 사용한다. 그에 반해 AutoRec은 Discriminative model이기에 rating 예측에 사용되는 평가 지표인 RMSE(Root Mean Squared Estimate)를 사용한다. MLE에 대한 내용은 여기를 참고하면 된다.
3. Optimization
RBM-CF는 모든 $v, h$ 조합에 대해 값을 모두 계산해야하기 때문에 정확한 계산을 위한 computational complexity는 exponential하게 된다(에너지 함수로 계산되는 수식이 지수함수로 구성되어 있기 때문). 계산이 복잡하기에 $p(v,h)$를 계산하는 Gibbs sampling의 step을 converge 할 때까지 수행하는 것이 아니라, n번만 돌려서(논문에서는 1번만 돌림) $p(v,h)$를 approximate하고, 그 값을 통해 $\sum_{v,h}p(v,h)v_i h_i$를 계산하는 방식을 Contrastive Divergence 알고리즘이라 한다. 그에 반해 AutoRec은 비교적 computatinoal이 빠른 gradient based backpropagation을 사용한다.
4. number of parameters
RBM-CF의 경우 discrete ratings에 대해서만 적용이 가능하고, 독립임을 가정했기 때문에 각각의 별도의 parameter를 추정하는 방식으로 진행된다. 그렇기 때문에 $r$을 예측하기 위해서는 $nkr$ 혹은 $mkr$의 parameter가 요구된다. 하지만 AutoRec은 $r$에 대해 agnostic하다고 표현했다. agnostic하다는 뜻은 parameter간 상호 공유가 가능하다는 것을 의미함으로 RBM-CF에 비해 보다 적은 parameter가 필요하다는 것을 뜻한다. 더 적은 paramter를 사용함으로써 메모리의 사용량은 더 적고, overfitting이 될 가능성 역시 줄어드는 경향이 존재한다.

본 논문에서는 추가적으로 MF 기반 모델인 Biased Matrix Factorization(BiasedMF), Local Low-Rank Matrix Factorization(LLORMA) 에 대해 추가 비교를 수행했다. 선정한 MF 기반 모델은 사용자와 아이템 간의 상호작용을 선형으로 표현하였지만, AutoRec의 경우 활성화 함수인 $g(\cdot)$을 Sigmoid로 사용함으로써 비선형까지 고려했기 때문에 선형, 비선형 간 성능차이를 파악하기 위해 비교 대상으로 MF 모델을 선정한 것으로 보인다.
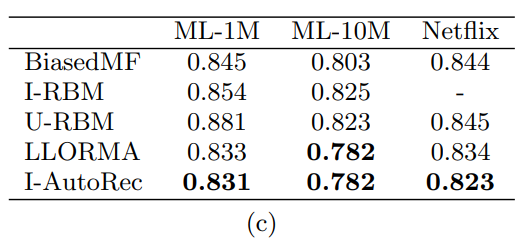

UBCF에 비해 IBCF의 성능이 좋은 것처럼 U-AutoRec보다는 I-AutoRec의 성능이 좋은 것을 확인할 수 있다. 본 논문에서는 RBM과 AutoRec 모두 일반적으로 User based보다 Item based의 성능이 좋게 나온 것을 확인하였고, 그 이유로는 아이템에 측정된 평점 수가 사용자가 아이템에 대해 측정한 평점 수 보다 많기 때문에(덜 sparse 하기 때문) 더 좋은 성능이 나온다고 했다. 또한 AutoRec의 모든 모델이 모든 RBM 보다 성능이 좋은 것을 확인했다.
한가지 신기한 점은 $f(\cdot), g(\cdot)$ 함수를 Sigmoid 대신 ReLU를 사용할 때 오히려 성능이 떨어졌다고 한다. 추가적으로 hidden unit의 수를 나타내는 $k$의 경우 size를 늘릴수록 좋은 성능을 보여주었는데, 본 논문에서는 $k=500$으로 설정하여 분석을 수행했다고 한다.