Contents
One-Class Collaborative Filtering (OCCF)은 user-item 쌍에서 positively-related를 식별하는 것을 목적으로 한다. positively-related 는 긍정적인 관련성을 의미하고, 사용자가 선호할 만한 제품을 찾는 것을 의미한다. 기존 연구에서는 Negative Sampling (NS)에 의존하여 이를 추출하였으나, 다양한 문제점이 존재한다. 본 논문에서는 NS의 문제점을 해결하기 위해 새로운 OCCF 기법인 BUIR을 제안한다.
1. Introduction
최근 Implicit Feedback만 사용하는 추천 시스템 연구에서 사용자의 선호도를 정확하게 예측하기 위해 OCCF에 초점을 둔 연구가 많이 진행되고 있다. OCCF는 적은 수의 관측된 상호작용(interaction)만을 사용함으로써 사용자가 가장 선호할 만한 제품을 찾는 것이 목적이다. 대부분의 OCCF 관련 논문은 유사도를 기반(e.g., inner product)으로 사용자가 제품과 상호작용이 있을 확률을 정의하고, 이를 통해 추천 성능을 측정한다.
그러나, OCCF의 문제에서는 negative interaction을 사용할 수 없기 때문에 관측되지 않은 값들은 모두 negative로 가정한다. 다시 말해, 모든 사용자에 대해서 아직 구매하지 않은 제품은 구매한 제품보다 덜 선호하는 것으로 간주한다. 따라서, 기존 연구에서는 이를 바로 Negative로 사용하거나 NS를 통해 확률적으로 Negative를 샘플링하여 연산량을 줄이는 형태로 진행하였다.
그러나, 기존 연구에서 사용하는 NS는 다음과 같은 문제점이 존재한다. 첫 번째, 데이터의 Sparsity 정도에 따라 효과가 달라진다. Positive Sample이 적을수록 Positive하지만 interaction이 없는 값이 많아져서, 실제로 Negative를 샘플링하기 어려워진다. 두 번째, NS가 어떻게 샘플링 되냐에 따라 모델의 수렴 속도가 달라진다. 예를 들어, non-uniform distribution으로 Negative를 추출하게 되면, 모델의 성능을 향상될 수 있지만, 많은 양의 사용자와 연산을 수행해야하기 때문에 속도가 저하된다.
본 논문에서는 위 문제를 해결하기 위해 새로운 OCCF 기법인 BUIR을 제안한다. BUIR은 모델을 학습할 때 NS가 필요하지 않으며, 모델의 핵심은 $(u, v)$ interaction이 주어졌을 때 $u$와 $v$의 유사도를 유사하게 인코딩하는 것이다. 그러나 단순히 Negative Supervision 없이 모델을 학습하게 되면 간단한 문제이기 때문에 빠르게 수렴하게 되고, Encoder는 입력값이 들어가면 모두 동일한 값을 출력하는 'Collapsed Solution' 이 된다.
본 논문에서는 Collapsed Solution이 end-to-end 학습 당시에 $u$와 $v$를 동시에 최적화할 때 발생하는 문제라 주장하고, 해당 방법 대신 Student teacher like network를 사용한다. 구체적으로 BUIR은 Bootstrap 방식을 사용하여 Online Encoder, Target Encoder로 구성된 두 가지 별개의 Encoder 네트워크를 사용한다. 실제 학습은 Online Encoder에서만 진행되고, Target Encoder에서 계산된 Gradient를 Online Encoder에 넘겨주어 값을 도출한다. 또한, 데이터의 희소성 문제를 해결하기 위해 Self-Supervised Learning을 통하여 Data Augmentation을 적용한다.
2. Related Work
본 논문에서는 OCCF와 Self-Supervised Learning을 통해 모델을 학습하고 있다. 2 장에서는 BPR Loss와 Contrastive Learning에서 사용하는 InfoNCE의 Loss의 수식만 간략하게 다룬다.
\[ \mathcal{L} = - \sum_{(u, v^p, v^n)} \in \mathcal{O} \phi( sim(u, v^p) > sim(u, v^n)) \]
$\mathcal{O} = \{ (u, v^p, v^n) | (u, v^p) \in \mathcal{R}, (u, v^n) \notin \mathcal{R} \} $은 Negative Pair와 Positive Pair로 이루어진 집합을 의미한다. $v^p$와 $v^n$은 각각 Positive, Negative를 의미하고, Positive는 실제 사용자가 클릭이나 구매를 한 제품을 의미하고, Negative는 사용자의 클릭이나 구매가 관측되지 않은 제품을 의미한다. $\phi$는 최적화 함수를 의미한다. 대표적인 최적화 기법이 바로 BPR이다.
Self-supervised Constrastive Learning은 대조 학습으로 불리며, Data Augmentation을 통해 Positive Pair와 Negative Pair를 생성하고 이를 이용하여 최적화하는 방식이다. 대표적인 Loss Function은 InfoNCE가 있다.
\[ \mathcal{L} = \sum_{x \in \mathcal{D}} \log \frac{\exp(\text{sim}(x, x^p))}{ \exp (\text{sim}(x, x^p)) + \sum_{x^n \in \mathcal{D} \backslash \{x\}} \exp (\text{sim}(x, x^n))} \]
Contrastive Learning은 Positive Pair는 유사도가 높도록 계산하고, Negative Pair는 유사도가 작도록 학습하는 방식이다.
3. BUIR: Proposed Framework
3.1 Problem Formuation
본 논문에서 사용하는 수식을 기술한다. $\mathcal{U} = \{u_1, ..., u_M \}$과 $\mathcal{V = \{ v_1, ..., v_n\} }$은 각각 사용자와 아이템에 대한 집합을 의미한다. 이때 user-item interaction은 $\mathcal{R} = \{ (u,v) | \text{user } u \text{ is interacted with item } v \} $가 된다. OCCF의 최종 목적은 사용자 $u$가 제품 $v$를 선호할 지에 대한 선호도 점수인 $s(u,v) \in \mathbb{R}$를 도출하는 것이다.
3.2 Bootstrapping the Representations
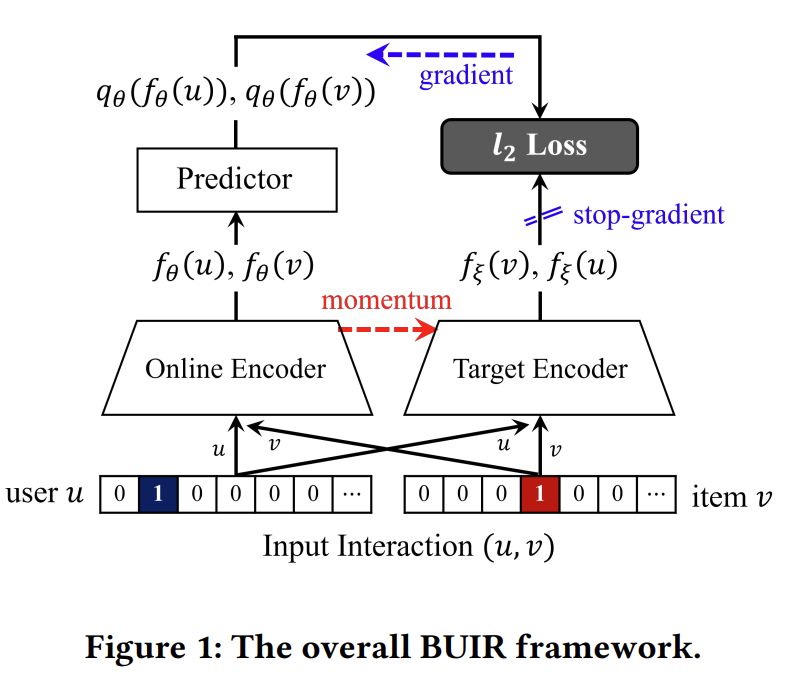
$f$를 사용자와 제품의 표현을 구성하기 위한 Encoder network라고 하자. Encoder 구조의 가장 간단한 예는 바로 Embedding Layer가 된다. Embedding Layer는 user-id와 item-id를 입력하면 D 차원의 embedding vector를 출력한다. BUIR는 같은 구조를 가진 Online Encoder $f_{\theta}$와 Target Encoder $f_{\xi}$로 구성되어 있다. BUIR는 Target Encoder의 output을 사용함으로써 Online Encoder를 학습하는 것이 핵심이다.
기존 연구에서 제안된 End-to-End 방식과 BUIR 간의 주요 차이점은 $f_{\theta}$와 $f_{\xi}$가 서로 다른 방식으로 업데이트 된다는 것이다. Online Encoder는 Output과 Target 사이의 오류를 최소화하는 방식으로 학습하지만, Target Network는 출력을 일관되게 유지하기 위해 momentum update를 기반으로 천천히 업데이트 한다. 이때 Predictor $q_{\theta} : \mathbb{R}^D \rightarrow \mathbb{R}^D $ 즉, Mean squared error를 통하여 BUIR의 Loss를 최소화 한다.
\[ \begin{equation} \begin{split} \mathcal{L}_{\theta, \xi} (u, v) & = l_2 [q_{\theta} (f_{\theta} (u)), f_{\xi} (v) ] + l_2 [ q_{\theta} (f_{\theta} (u)), f_{\xi} (u) ] \\ \\ & \approx -\frac{q_{\theta} (f_{\theta} (u))^T f_{\xi} (v)}{|| q_{\theta} ( f_{\theta}(u)||_2 || f_{\xi} (v) ||_2 } - \frac{ q_{\theta} (f_{\theta} (v))^T f_{\xi} (u) }{||q_{\theta} (f_{\theta} (v)) ||_2 ||f_{\xi} (u)||_2 } \end{split} \end{equation} \]
$l_2[x, y]$는 $l_2$ 정규화를 의미한다. BUIR는 이때 $f_{\theta}(u)$와 $f_{\xi}(v)$가 유사한 값을 띄도록 $f_{\theta}(v)$를 업데이트 한다. Online Encoder와 Target Encoder 의 학습은 Momentum 방식으로 진행되며 아래의 수식을 따른다.
\[ \begin{equation} \begin{split} \theta & \leftarrow \theta - \eta \cdot \nabla_{\theta} \mathcal{L}_{\theta, \xi} \\ \\ \xi & \leftarrow \tau \cdot \xi + (1 - \tau) \cdot \theta. \end{split} \end{equation} \]
$\eta$는 Learning Rate를 의미하고, $\tau \in [0, 1]$는 Momentum Coefficient를 의미한다. 위 손실 값은 $\theta$와 $\xi$에 대해 Collapsed Solution을 제공한다. 이는 두 Encoder가 모든 사용자와 제품에 대해 동일한 표현을 생성한다는 것을 의미한다. 이와 같은 이유로 $f_{\theta}$와 $f_{\xi}$를 최적화 하게 될 경우 Collapsed Solution이 도출될 수 밖에 없다. 이러한 문제를 극복하기 위해 본 논문에서는 각각의 Encoder를 서로 다른 방식으로 학습하여 최적화 한다. Target Encoder의 경우 $\theta - \xi$를 통해 최적화하고, Online Encoder의 경우 $(-\nabla_{\theta} \mathcal{L}_{\theta, \xi})$를 통해 최적화를 한다. 이렇게 하면 두 인코더가 모두 같은 Collapsed Solution으로 수렴되는 것을 방지할 수 있다.
3.3 Top-K Preferred Item Prediction
Top-K 방식은 사용자가 가장 선호하는 상위 K 개의 제품을 추천하기 위해 사용되는 방식이다. 예를 들어, 제품이 100개 있는 경우 100개의 제품을 유사도를 기준으로 내림차순으로 정렬하고 상위 K개의 제품을 추천한다. 만약 상위 K개의 제품을 선택하지 않고, 전부 추천하게 되는 경우 사용자의 선호도를 반영했다고 할 수 없기 때문에 최근에는 K=10, K=20 등을 설정하여 제품을 추천한다. 유사도를 계산하는 수식은 아래와 같다.
\[ s(u, v) = q_{\theta} ( f_{\theta} (u))^T f_{\theta} (v) + f_{\theta}(u)^T q_{\theta} (f_{\theta} (v)) \]
이때 수식을 살펴보면 오직 Online Encoder의 값을 통해서만 선호도 점수를 도출한다.
3.4 Neighbor-based Data Augmentation
본 논문에서는 Self-Supervised Contrastive Learning을 통해 Data Augmentation을 수행한다. 이분 그래프(bipartite)에서는 노드 간의 연결이 엣지로 구성되어 있기 때문에 해당 노드의 하위 집합, 즉, 이웃을 이용하여 Data Augmentation을 수행한다.
\[ \psi(u, \mathcal{V}_u) = (u, \mathcal{V}^{\prime}_u ), \quad \text{where } \mathcal{V}^{\prime}_u \sim \{ \mathcal{S} | \mathcal{S} \subseteq \mathcal{V}_u \} \]
\[ \psi(u, \mathcal{U}_v) = (v, \mathcal{U}^{\prime}_v, \quad \text{where } \mathcal{U}^{\prime}_v \sim \{ \mathcal{S} | \mathcal{S} \in \mathcal{U}_v \} \]
$\mathcal{V}^{\prime}_u$는 사용자 이웃의 부분 집합 중 하나를 의미한다. $\psi$는 Augmentation Function을 의미한다. 사용자가 입력으로 들어왔을 때 사용자 이웃의 부분 집합 중 하나를 사용하는 것이다. 이때 3.2절과 유사하게, Online Encoder는 $\mathcal{L}_{\theta, \xi} (\psi(u, \mathcal{V}_u), \psi (v, \mathcal{U}_v))$를 최소화 하는 방향으로 학습한다.
4. Experiments
4.1 Experimental Settings
본 논문에서는 기존 연구에서 성능이 우수하다고 알려진 BPR, NeuMF, CML, SML, NGCF, LGCN, M-VAE, CFGAN 등의 모델을 이용하여 성능을 비교하였다. 본 논문에서는 다양한 환경에서 성능을 비교하기 위해 각 사용자에 대한 특정 비율의 상호작용을 포함하는 데이터셋을 구성하였다. 이때 특정 비율은 $\beta$로 표기하고 $\beta = 10%$인 경우 10%만 학습으로 사용하는 것을 의미한다. 나머지는 Valid, Test 셋으로 동일한 비율로 분할하여 사용하며, 총 5번의 시행을 통해 평균값을 계산한다.
4.2 Comparison with OCCF Methods
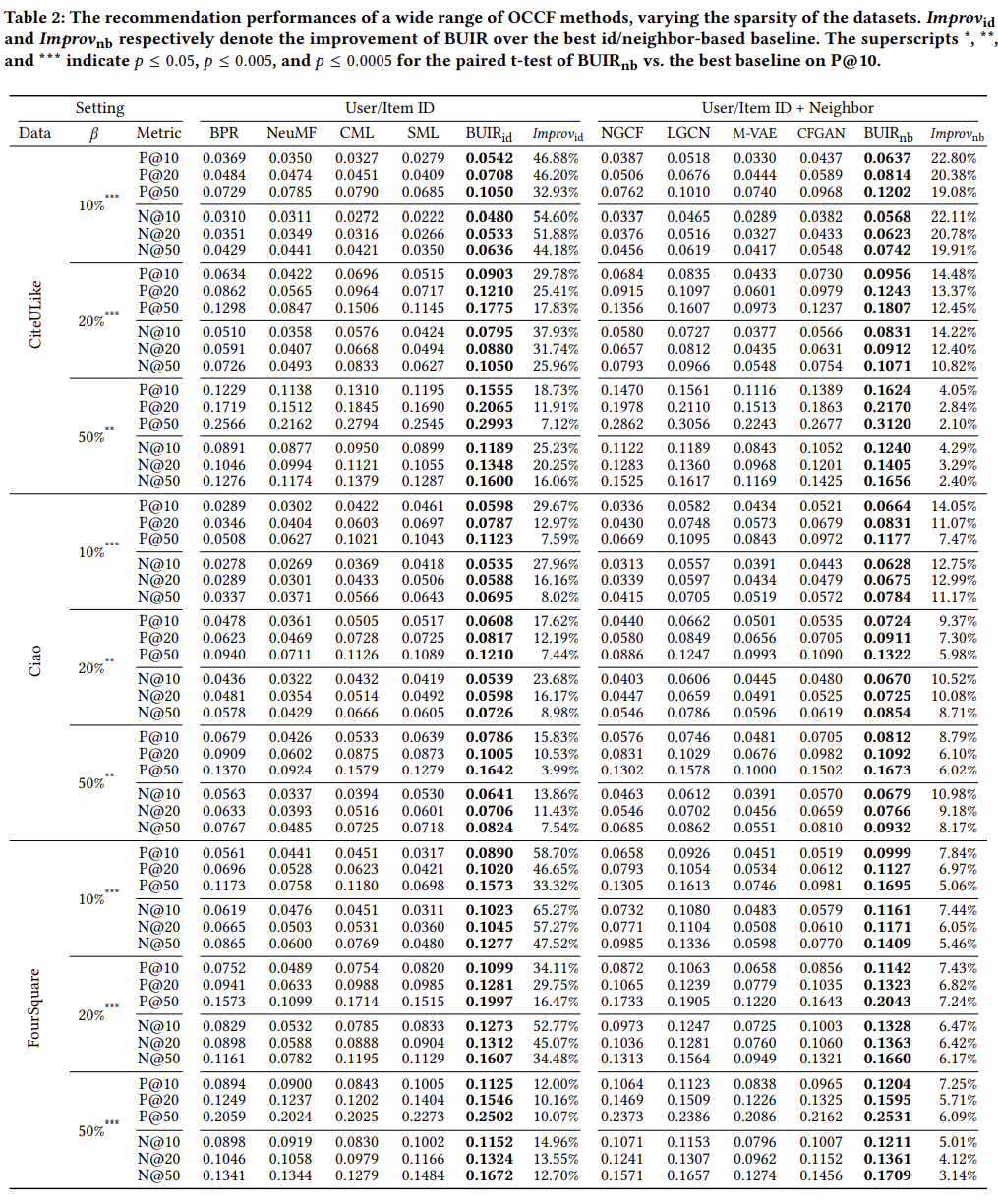
실험 결과는 Table2와 같으며, 본 논문에서 제안하는 BUIR의 성능이 가장 우수한 것을 확인할 수 있다. 모든 데이터셋에 대해서 유의미한 정도의 차이를 보이고 있다. 또한, 데이터가 더 sparse한 경우에 성능이 더욱 우수한 것을 확인할 수 있다. $\text{BUIR}_{id}$는 Embedding Layer에서만 BUIR을 사용한 것을 의미한다. $\text{BUIR}_{id}$는 LightGCN 방법에서 BUIR을 적용한 것을 의미한다.
4.2.1 Effectiveness of BUIR_id
모든 데이터셋에서 $\text{BUIR}_{id}$의 성능이 우수한 것을 확인할 수 있다. $\text{BUIR}_{id}$는 실제 사용자가 구매하지 않은 제품 중에서 구매할 가능성이 높은 제품 간의 상호작용을 사용할 가능성이 높기 때문에 데이터가 Sparse할 경우 보다 우수한 성능을 발휘하고 있다.
4.2.2 Effectiveness of BUIR_nb
$\text{BUIR}_{nb}$도 역시 가장 우수한 성능을 보여주고 있다. 구체적으로 NGCF, LightGCN 등과 같이 이웃 기반으로 학습하는 모델과 성능을 비교한 결과, 기존의 단순히 Embedding 만 사용하여 학습하는 모델에 비해 보다 성능이 우수한 것을 확인할 수 있다.
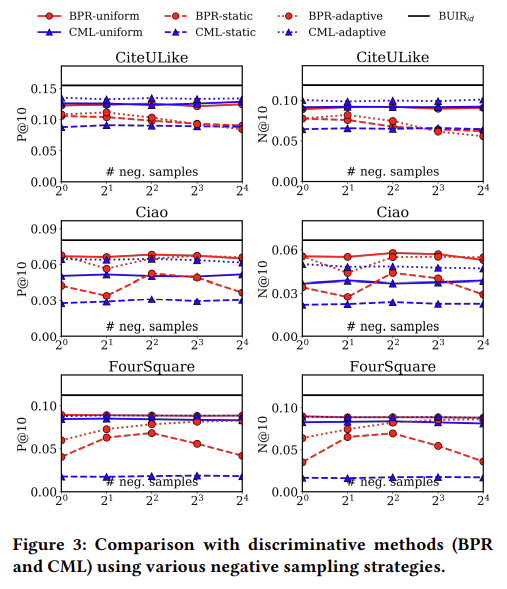
4.2.3 Comparison of different negative sampling strategies
Negative Sampling을 어떻게 하냐에 따라서 추천 시스템의 성능이 달라질 수 있다. 따라서, 본 논문에서는 베이스라인의 모델에서 NS를 다양한 방법으로 사용하여 추천 성능을 도출하고, 이를 $\text{BUIR}$와 비교하엿다. 비교결과, 본 논문에서 제안하는 모델의 성능이 우수한 것을 확인할 수 있다.
4.3 Ablation Study
$\text{BUIR}$ 에서 각 구성 요소 즉, Predictor, Neighbor, Augment 의 효율성을 검증하기 위해 각각의 요소를 제거하여 아래의 표와 같은 실험을 진행하였다. 실험 결과, Predictor, Neighbor, Augment 각각 추가할 때마다 성능이 개선되는 것을 확인할 수 있다.

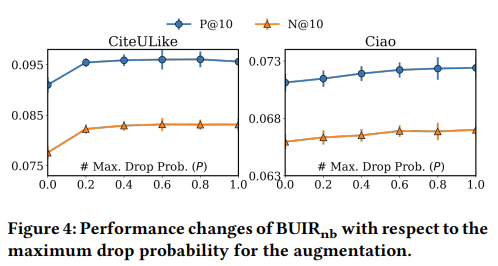
4.4 Effect of Neighbor Augmentation
Data Augmentation Function $\phi$의 효과에 대한 성능을 측정하기 위해 Drop rate를 달리하여 실험을 진행하였다. 실험 결과, Drop Rate를 높이더라도 성능이 증가하는 것을 확인할 수 있다. 이를 요약하면, Neighbor Augmentation을 사용하면, Augmentation View를 활용하여 데이터의 희소성 문제를 완화할 수 있어 성능이 향상된다.
4.5 Evaluation on Representation Quality
$\text{BUIR}$을 통해 도출된 Representation의 성능을 검증하기 위해 , 다운스트림(Downstream) 태스크를 진행하여 실험을 진행하였다. 실험 결과, $\text{BUIR}_{id}$와 $\text{BUIR}_{nb}$의 성능이 우수한 것을 확인할 수 있다.

4.6 Sensitivity Analysis
$\text{BUIR}$에는 Latent Dimension $D$, momentum coefficient $\tau$, predictor $q_{\theta}$가 존재한다. 이를 달리하여 성능이 얼마나 변화하는지 실험하였다. 실험결과, $\tau$는 [0.0, 1.0]에서 가장 우수한 성능을 발휘하고 있다. $\tau$가 높을수록 Encoder가 제대로 학습하는 것을 의미한다. $q_{\theta}$는 Layer의 수가 하나인 경우에 가장 우수한 성능을 발휘하고 있다. 이는, Layer의 수가 증가할수록 두 Encoder를 최정화하는 것이 어렵기 때문이라고 판단하였다.

5. Conclusion
본 논문에서는 사용자와 제품의 표현을 학습하기 위한 새로운 프레임워크인 $\text{BUIR}$를 제안하였다. BUIR는 Bootstrap 방식을 사용하여 cross-prediction error를 최소화한다. 이는 부분적으로 관찰된 긍정적인 상호작용만 사용하도록 하고, NS 를 사용하지 않아도 된다. 또한, Contrastive Learning을 통해 Data Augmentation 함으로써 데이터의 희소성 문제를 일부 완화한다. 마지막으로, 다양한 데이터와 다양한 실험을 통해 $\text{BUIR}$의 성능이 기존 모델에 비해 우수한 성능을 보여주는 것을 확인하였다.