Contents
본 논문은 Contrastive Learning (CL)을 추천 시스템에 적용한 논문이다. SIGIR'22에서 발표된 컨퍼런스 논문이며, 이전에 제안된 Self-Supervised Learning과는 다른 구조를 띄는 simGCL을 제안하였다. 본 논문에서 제안하는 simGCL이 어떤 것인지 알아보자.
1. Introduction
최근 딥러닝에서 다시 Contrastive Learning (CL)을 적용한 연구들이 제안되고 있다. CL은 라벨이 지정되지 않은 데이터에서 일반적인 특징을 추출하고, 정규화하는 것으로 인해 여러 분야에서 우수한 성능을 발휘하였다. 이는 annotation이 필요하지 않기 때문에, 추천 시스템의 희소성(Sparsity) 문제를 해결할 수 있다. 그로 인해, CL을 추천 시스템에 적용하고자 하는 연구들이 많이 제안되었다. 대표적인 연구는 SGL이 있으며, SGL은 처음으로 추천 시스템에 CL을 적용한 논문이다. 이는 섭동 이론(perturbations Theory)을 통해 이분 그래프(Bipartite Graph)를 증강(Augmenation)하여 실험을 진행하였다. 이때 섭동 이론은 테일러 급수처럼 여러 데이터를 통해 값을 찾는 것을 의미하며, SGL에서는 node dropout, edge dropout을 통해 생성된 graph perturbations으로 관측되지 않은 노드의 값을 찾는 것을 의미한다. [Figrue 1]

이처럼 CL이 추천 시스템에 고무적인 결과를 도출함에도 불구하고, 명확하게 왜 성능이 좋아지는 지에 대한 설명을 얻을 수가 없다. 직관적으로 SGL은 서로 다른 graph augmentation를 통해 실제 user-item interaction을 본질적인 정보를 포착할 수 있다고 가정한다. 그러나 일부 연구에서는 edge dropout rate를 0.9로 설정하더라도 학습이 제대로 되는 것을 확인하였다. 이로써, 다음과 같은 연구 질문을 던질 수 있다. "추천 시스템에 CL을 적용할 때 Graph Augmentation이 정말 필요한가?"
연구 질문에 답하기 위해 본 연구에서는 graph augmentation가 있는 경우와 없는 경우의 성능을 비교하였다. 실험 결과, augmenation이 있는 경우와 없는 경우가 거의 유사한 것으로 확인되었다. 그 후, non-CL과 CL 기법의 표현(Representation)을 시각화하고, 성능과 연관시킴으로써 추천 성능에 실제로 중요한 것은 graph augmenation이 아니라 CL의 Loss인 것을 알게 되었다. Contrastive Loss 함수인 InfoNCE는 Graph Augmenation이 적용되더라도 더 균일한 user-item 표현을 학습한다. 즉, Augmentation보다 CL Loss가 더 중요하다는 것을 의미한다.
그러나, Graph Augmentation이 장점이 없는 것은 아니다. Best Seller나 Influence, Heavy User 들로 인해 추천 제품이 편향되는 것을 Node Dropout, Edge Dropout을 통해 어느정도 완화할 수 있다. 게다가, 효과적이지는 않지만, 원래 그래프 학습보다는 CL을 적용한 경우 성능이 개선되었다. 그러나, Dropout을 수행할 때 직접 Graph를 만들어주어야 되기 때문에 시간이 많이 소모된다. 추가적으로, 노드나 엣지가 잘리기 때문에 실제 그래프와 Augmented 그래프 간의 차이가 존재할 수 있기 때문에 그로 인해 학습이 제대로 안될 수 있다.
그렇다면, 보다 "효율적인 Graph Augmentation 방법은 없을까?" 본 논문에서는 표현의 분포의 균일성이 핵심 포인트 인 것을 확인하고, 균일성을 더 제어할 수 있는 Augmentation 방법이 없는 간단한 CL 방법을 제안한다. 본 논문에서는 Node Dropout, Edge Dropout 등과 같은 방법 대신 그래프에 노이즈를 추가하였다. 서로 다른 노이즈를 그래프에 추가할 경우 contrastive view에서는 분산이 생성되는 반면에, 학습이 가능한 invariance는 제어된 크기로 인해 여전히 유지된다. 이때 contrastive view는 positive pair와 negative pair를 의미한다. 서로 같은 positive pair의 경우 표현이 가깝게, negative pair의 경우 다르게 학습하는 것이다. 이를 Graph Augmentation에 비해 노이즈 버전이 임베딩 공간을 보다 균일한 분포로 직접 정규화하므로 구현하는 것이 훨씬더 효율적이다.
위 내용을 정리하면 본 논문의 메인 Contribution은 아래와 같다.
- CL이 추천 성능을 높일 수 있는 이유를 실험적으로 밝히고 Graph Augmentation보다 InfoNCF 손실이 결정적인 요인인 것을 확인하였다.
- 노이즈를 추가하는 방법을 통해 균일도를 원활하게 조절할 수 있게 되어 Graph Augmenation 없는 CL 추천 방법을 제안하였다.
- simGCL이 3개의 벤치마크 데이터셋에서 추천 성능과 효율성 측면에 Graph Augmentation 기반 기법보다 본 논문에서 제안하는 simGCL의 우수한 것을 검증하였다.
2. Investigation of Graph Contrastive Learning in Recommendation
2.1 Graph CL for Recommendation
CL 기법은 Data Augmentation을 사용하여 추천 시스템에 적용한 경우가 많다. Augmentation을 통해 데이터를 생성하고, 이를 학습하여 편향을 줄이려는 것이 목적이다. 본 연구에서는 추천 시스템에서 SoTA를 달성한 SGL 기법을 사용하여 실험을 구성하였다. SGL은 Node Dropout, Edge Dropout 등을 통해 데이터를 Augmentation하고 CL 기법에 InfoNCE를 적용하여 다음과 같이 Loss를 측정한다.
\[ \mathcal{L}_{joint} = \mathcal{L}_{rec} + \lambda \mathcal{L}_{cl} \]
InfoCNE는 추천 시스템을 통한 Loss인 $\mathcal{L}_{rec}$와 CL 기법을 통한 Loss인 $\mathcal{L}_{cl}$로 구성되어 있다. $\mathcal{L}_{cl}$은 아래와 같이 계산된다.
\[ \mathcal{L}_{cl} = \sum_{i \in \mathcal{B}} -\log \frac{\exp(z^{\prime T}_i z^{\prime \prime}_i / \tau )}{\sum_{j \in \mathcal{B}} \exp ( z^{\prime T}_i z^{\prime \prime}_i / \tau ) } \]
$i, j$는 각각 배치 $\mathcal{B}$에서의 사용자와 제품을 의미한다. $z^{\prime} ( z^{\prime \prime})$은 서로 다른 dropout based graph augmentation으로 부터 학습된 후 $L_2$ 정규화된 $d$ 차원의 노드 표현(Node Representation)을 의미한다. 그리고 $\tau > 0$는 temperature를 의미한다. 이때 같은 두 노드의 표현이 유사하도록 만들고, 서로 다른 노드의 표현은 다르도록 하는 것이 목적이다. 즉, $ z^{\prime T}_i z^{\prime \prime}_i$는 가깝도록 학습하고, $z^{\prime T}_i z^{\prime \prime}_j$는 멀어지도록 학습하는 것이다. user-item Graph로부터 표현을 학습하기 위해, SGL은 널리 사용되는 LightGCN을 이용하여 아래와 같이 학습한다.
\[ E = \frac{1}{1 + L} ( E^{(0)} + \tilde{A}E^{(0)} + \cdots + \tilde{A}^L E^{(0)} ) \]
$E^{(0)} \in \mathbb{R}^{|N| \times d}$은 node embedding의 초기 값을 의미하고, $|N|$는 노드의 수를 의미한다. $L$은 Layer의 수를 의미하고, $\tilde{A} \in \mathbb{R}^{|N| \times |N|}$는 정규화된 무향 그래프의 인접행렬을 의미한다.
2.2 Necessity of Graph Augmentation
CL 기반 추천 시스템이 작동하는 방식을 이해하기 위해서는 먼저 SGL에서 그래프 확장이 왜 필요한 지에 대해서 알아야 한다. 이를 확인하기 위해 먼저, Graph Augmentation이 없는 경우의 CL의 수식을 아래와 같이 표현하였다.
\[ \mathcal{L}_{cl} = \sum_{i \in \mathcal{B}} -\log \frac{ \exp(1/\tau)}{\sum_{j \in \mathcal{B}} \exp(z^T_i z_j / \tau )} \]
이때 $\mathcal{L}_{cl}$은 원래의 user-item Graph를 통해서만 표현을 학습하기 때문에, $z^{\prime}_i = z^{\prime \prime}_i = z_i$가 된다. 그 후 Graph Augmentation을 한 모델과 하지 않은 모델 간의 성능을 비교하였다. 실험 과정은 4.1절에서 자세히 다룬다. 실험 결과, SGL-WA(Without Augmentation) 모델의 성능이 다른 SGL-ND, SGL-ED 모델에 비해 성능이 낮은 것을 확인할 수 있다. CL Only는 추천시스템의 Loss는 사용하지 않고 오로지 CL Loss만 사용한 경우다.
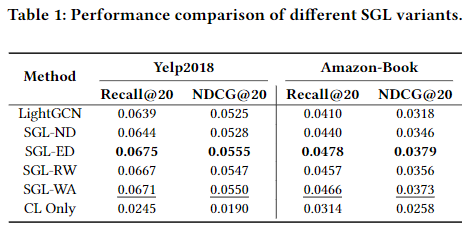
SGL를 제안한 논문에서는 LightGCN과 성능을 비교하였으며, 실험 결과 SGL의 성능이 LightGCN에 비해 우수한 것을 확인하였다. 따라서, CL의 효율성이 검증되었다. 본 연구에서의 실험 결과, SGL-WA의 성능이 LightGCN보다 우수하고, 심지어는 SGL-ND, SGL-RW 보다 성능이 우수한 것을 확인하였다. 즉, CL Loss 만을 사용한 경우에도 성능이 향상되고, Graph Augmentation으로 인한 성능 개선은 미미한 것으로 확인되었다.
실험 결과를 바탕으로 다음과 같은 결론을 도출할 수 있다. Node Dropout과 Random Walk의 경우 주요 노드와 관련이 높은 엣지를 드롭할 가능성이 매우 높아 상관관계가 있는 subgraph를 연결되지 않은 조각들로 쪼개어 원본 그래프를 크게 왜곡해서 발생하는 문제라고 추측한다. 이를 통한 Graph Augmentation은 같은 노드 간의 표현이 같도록 학습하는 CL 방법에서는 오히려 부정적인 영향을 미칠 수 있기 때문이다. 반면에, Edge Dropout의 경우 원래 그래프를 크게 왜곡할 가능성이 낮아 다른 모델에 비해 이점을 가지기 때문에 성능이 우수한 것으로 확인된다. 그러나, Edge Dropout 역시도 모델을 학습할 때 인접 행렬을 재구성해야 하기 때문에 시간이 많이 소요된다. 따라서, 이를 극복하기 위한 대안이 제시되어야 한다.
2.3 InfoNCE Loss Influence More
기존 연구에서 InfoNCE를 최적화할 경우 positive pairs의 특징이 잘 정렬되고, hypersphere가 잘 정규화된 분포를 가지는 균일성을 띄는 것으로 확인했다. 위 방식이 추천 시스템에서도 동일한 패턴을 보이는 지 확인하기 위해 이에 대한 문제를 조사하였다.
실험 결과, LightGCN은 일부 공간에 클러스터링 되어 있는 것을 확인할 수 있고, SGL-WA, SGL-ED의 경우 LightGCN에 비해 조금 더 균일한 것을 확인할 수 있으며, Density 또한 덜 sharp 한 것으로 확인된다. 4 번째 그림의 경우 오직 CL Loss만 사용한 경우를 의미하며, 이때 가장 균일한 분포를 띄는 것을 확인할 수 있다.

본 논문에서는 LightGCN에서 특징들이 군집화를 이루는 이유에 대해서 다음과 같이 설명한다. 첫 번째는 LightGCN의 메세지 전달 메커니즘이다. Layer의 수가 증가할 수록 노드들의 표현은 주변 노드들과 비슷해진다. 두 번째는 추천 시스템에서의 데이터에 대한 문제다. LightGCN의 경우 아래와 같은 BPR Loss 를 사용한다.
\[ \mathcal{L}_{rec} = -\log(\sigma(e^T_u e_i - e^T_u e_j )) \]
BPR Loss는 관측된 정보와 관측되지 않은 정보 간의 차이를 최대화 하는 형태로 학습된다. 이때 미분을 수행하면 $\nabla e_u = -\eta (1-s)(e_i - e_j) $가 도줄된다. $\eta$는 learning rate를 말하고, $s = \sigma (e^T_u e_i - e^T_u e_j)$가 된다. 추천 시스템은 일반적으로 Pow-Law Distirbution, 즉, Long-tail 을 가진 Distribution를 띄는데, 임베딩을 학습할 때 기본적으로 $ - \nabla e$ 방향으로 학습하게 된다. 그렇게 되면 당연히 메세지를 전달할 때 클러스터링 문제를 더욱 악화할 수 밖에 없다. 이는 representation degeneration을 야기한다. 우리는 위에서 다룬 $\mathcal{L}_{cl}$을 아래와 같이 풀어서 다른 식으로 도출할 수 있다.
\[ \mathcal{L}_{cl} = \sum_{i \in \mathcal{B}} -1 / \tau + \log \left ( \exp(1/\tau) + \sum_{j \in \mathcal{B} / \{ i \}} \exp( z^T_i z_j / \tau ) \right ) \]
$ -1 / \tau$는 상수이기 때문에 CL Loss를 최적화할 때에는 서로 다른 Node Embedding 간의 코사인 유사도가 최소가 되는 방향으로 학습하게 된다. 이는 Recommendation Loss의 영향을 받는 경우에도 균일한 분포로 만들어질 것이다. 해당 결과를 바탕으로 분포의 균일성이 SGL에서 추천 성능에 결정적인 영향을 미치는 기저 요인이라는 것을 확인할 수 있다. 균일한 표현 분포가 노드의 고유한 특성을 보존하고 일반화 능력을 향상시킬 수 있기 때문에 CL Loss를 최적화하는 것은 편향을 제거할 수 있는 방법 중 하나라고 볼 수 있다.
3. simGCL: Simple Graph Contrastive Learning for Recommendation
본 논문에서는 학습된 표현의 균일성을 조정함으로써 최적의 성능에 도달할 수 있다고 추측하고, 이를 위한 SimGCL (Simple Graph Contrastive Learning method) 모델을 제안한다.
3.1 Motivation and Formulation
Node Dropout, Edge Dropout 처럼 그래프 구조를 조작하는 것은 다루기 힘들 뿐더러, 시간이 많이 걸리기 때문에 본 논문에서는 아래와 같이 임베딩 공간에서 노이즈를 주어 균일성을 조정하고자 한다.
\[ e^{\prime}_i = e_i + \Delta^{\prime}_i, \quad e^{\prime \prime}_i + \Delta^{\prime \prime}_i \]
이때 $\Delta^{\prime}$과 $\Delta^{\prime \prime}$은 $||\Delta||_2 = \epsilon, \ \text{and} \ \Delta = \bar{\Delta} \odot \text{sign}(e_i), \ \bar{\Delta} \in \mathbb{R}^d ~ U(0, 1)$을 따르는 노이즈 벡터(Noise Vector)를 의미한다.

첫 번째 제약 조건은 $\Delta$의 크기를 제어한다. 이때 $\Delta$는 반지름이 $r=\epsilon$인 hypershpere의 점과 동일하다. 두 번째 제약 조건은 $\Delta^{\prime}$과 $\Delta^{\prime \prime}$이 hyperoctant에 있어야 한다. 그렇게 되면, 노이즈를 추가해도 $e$의 편차가 크게 발생하지 않는다.
본 논문에서는 실험을 하기 위해 LightGCN의 graph encoder 구조를 가지고 와서 노드의 정보를 Propagate하고, 단순한 구조와 효율성을 이용하여 노이즈로 인한 편차의 영향을 증폭시켰다. 각각의 Layer마다 서로 다른 크기의 노이즈를 부여하였으며, 이를 수식으로 표현하면 아래와 같다.
\[ E^{\prime} = \frac{1}{L} ( ( \tilde{A} E^{(0)} + \Delta^{(1)} ) + (\tilde{A} ( \tilde{A} E^{(0)} + \Delta^{(1)} ) + \Delta^{(2)} ) + \cdots \]
\[ + \ (\tilde{A}^L E^{(0)} + \tilde{A}^{(L-1)} \Delta^{(1)} + \cdots + \tilde{A} \Delta^{(L-1)} + \Delta^{(L)} )) \]
3.2 Regulating Uniformity
SimGCL에는 $\lambda$와 $\epsilon$ 두 가지 하이퍼파라미터가 존재한다. $\epsilon$은 $\lambda$를 조절함으로써 조절이 가능하기 때문에 엄밀히 따지면 $\lambda$만 존재한다. $\epsilon$을 조정함으로써 Augmentation 표현이 얼마나 원래의 표현에서 벗어낫는지를 직접 제어할 수 있다. 만약 $\epsilon$이 커진다면 Augmentation 된 표현이 원본 데이터와 멀리 떨어져 있을 때 표현이 노이즈에 의해 상당히 많은 영향을 받을 수 있기 때문에 더 균일한 분포를 만들 것이다. 균일 분포에 의해서 생성된 노이즈를 통해 실제 값과 대조함으로써 원래의 노드 표현이 보다 균일하게 정규화되는 것을 실험을 통해 검증하였다. 균일성을 측정하기 위해 아래의 수식과 같은 RBF(Radial Basis Function) 커널을 사용한다.
\[ \mathcal{L}_{\text{uniform}} (f) = \log \underset{u, v, \sim p_{node}}{\underset{i, i, d}{\mathbb{E}}} e^{-2 || f(u) - f(v) ||^2_2} \]
이때 $f(u)$는 $L_2$ 정규화된 $u$의 임베딩을 출력한다. 본 논문에서는 인기 있는 제품을 선정하고, 무작위로 5천명의 사용자를 선택해 SGL과 SimGCL 을 통해 계산된 표현들의 균일성을 계산하였다.

$\mathcal{L}_{\text{uniform}}$은 낮을수록 좋은 값을 띈다. 초반에 낮은 Loss 값을 보이는 이유는 본 논문에서 Xavier initialization을 사용했기 때문이다. 실제 학습은 peak를 찍은 후 안정되는 부분을 보면 된다. SimGCL의 경우 낮은 $\epsilon$일 때보다 높은 $\epsilon$일 때 학습이 잘 되는 것을 확인할 수 있으며, SGL의 경우 상대적으로 수렴 속도가 느린 것을 확인할 수 있다.
3.3 Complexity
$\rho$는 얼마만큼 엣지를 가지고 있을지에 대한 비율을 의미한다. 만약 dropout rate가 0.1이라면 $\rho$는 0.9가 된다. CL을 수행하기 위해서는 Graph Augmentation이 필요하기 때문에, 저만큼의 복잡도에 대한 정보가 추가로 필요하다. 반면에 SimGCL의 경우 Graph Convolution을 수행할 때 노이즈를 추가해 CL을 수행하기 때문에 $\mathcal{O}(6|E|Ld)$가 된다.

시간 복잡도만 본다면 SimGCL이 왜 효율적이라고 하는지 모를 수 있다. Graph perturbation 연산은 CPU에서 연산이 수행된다. 반면에 본 논문에서 제안하는 SimGCL의 경우 Graph Convolution 연산을 수행할 때 노이즈를 만들어 사용하기 때문에 GPU에서 연산이 가능하다. 따라서, 매우 효율적으로 연산이 가능하다.
4. Experimental Results
4.1 Experimental Settings
본 논문에서는 Douban-Book, Yelp2018, Amazon-Book 데이터를 활용하여 실험을 진행하였다. 실험 결과를 비교하기 위해 벤치마크 모델은 Mult-VAE, DNN+SSL, BUIR, MixGCL을 사용하였다. 자세한 파라미터 세팅은 아래의 그림으로 대체한다.

4.2 SGL vs SimGCL: From a Comprehensive Perspective
4.2.1 Performance Comparison
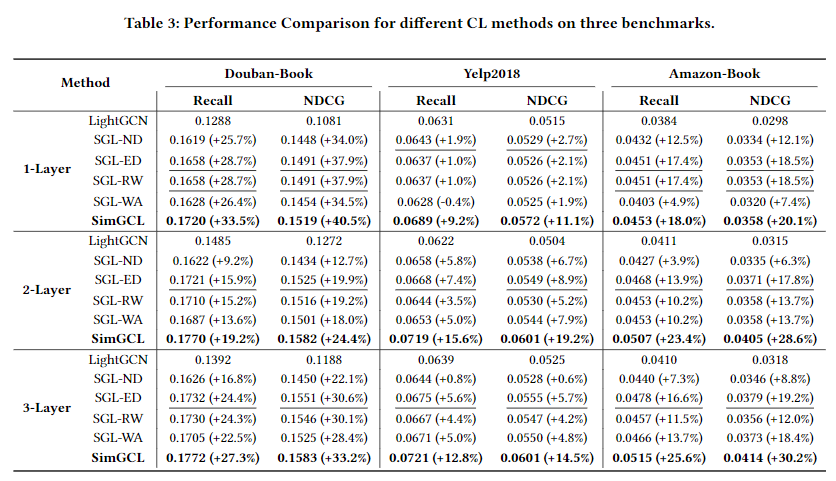
SGL과 SimGCL의 성능 비교결과, SGL과 SimGCL 모든 결과가 LightGCN 보다 우수한 성능을 보이고 있다. Bouban-Book 데이터셋에서 가장 큰 성능 개선을 보여주었으며, Layer의 수가 1인 경우에 가장 성능이 좋았다. 본 논문에서는 Layer를 3개 까지만 쌓아서 사용했는데, SGL과 SimSGL은 일반적으로 Layer가 낮을 때 성능이 우수한 것으로 확인되었기 때문이다.
SGL-ED의 경우 성능이 우수하지만, SGL-ND의 경우 SGL-RW 에 비해 성능이 저하되는 것을 볼 수 있다. 이는, CL Loss가 성능 향상에 주요한 원인인 것에 반하여, Graph Augmentation은 예상만큼 효과적이지 않을 수 있다는 것을 의미하고, 일부는 성능을 저하시킬 수 있다는 것을 의미한다.
4.2.2 Convergence Speed Comparison
LightGCN의 경우 가장 간단하기 때문에 제일 먼저 수렴하는 것을 확인할 수 있으나, Douban-Book의 경우 수렴 값도 제일 높은 것으로 확인된다. SimGCL의 경우 GCL에 비해서는 수렴속도가 빠른 것을 확인할 수 있다.

4.2.3 Running Time Comparison
본 논문에서는 RTX 2080Ti를 사용하여 실험을 진행하였다. LightGCN의 Runtime 속도를 기준으로 비교하였다. SimGCL은 SGL-WA 만큼 빠르지는 않지만 그래도 SGL-ED에 비해서는 빠른 속도를 보여주고 있다.

4.2.4 Ability to Debias
본 논문에서 사용하는 노이즈 기법이 실제 편향을 낮출 수 있는지 확인하고자 다음과 같은 실험을 진행하였다. 먼저 구매/클릭 횟수가 적은 80%에 위치한 항목은 'Unpopular'으로 표시하고, 상위 5% 항목은 'Popular'으로 표시하였으며, 나머지는 'Normal'로 표시하였다. SimGCL 은 다른 항목들에 비해 인기 있지 않은 제품을 보다 많이 추천하는 것으로 확인된다. 따라서, Debias 한 것으로 확인된다.

LightGCN은 별도의 처리 없이 제품을 추천하기 때문에 모델을 학습하는 과정에서 인기 있는 제품의 영향을 많이 받게 된다. 반면에, SGL과 SimSGL의 경우 CL 학습을 통해 인기 있는 제품을 없해거나, 제품 간의 균일성을 통해 인기 있는 제품만 추천 되는 것을 방지할 수 있어서 Long-tail Distribution을 가진 추천 시스템 분야에서 매우 효과적으로 활용될 수 있다.
4.3 Parameter Sensitivity Analysis
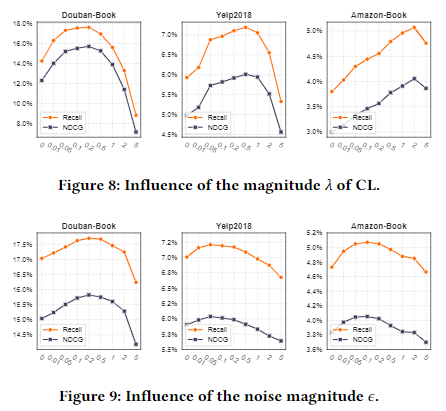
본 논문에서는 $\lambda$와 $\epsilon$ 두 개의 하이퍼파라미터가 존재한다. 각각의 하이퍼파라미터의 값에 따른 성능을 비교하고자 한다. $\lambda$의 경우 0.1, 0.2 인 경우에 가장 성능이 우수한 것을 확인할 수 있다. 그러나, Amazon-Book 에서는 $\lambda$의 값이 2까지 계속 성능이 개선되는 것을 확인할 수 있다. Amazon-Book의 경우 제품의 수가 많기 때문에, CL Loss의 값을 키워도 성능이 개선되는 것을 의미한다. [Figure 8]의 경우 $\lambda$가 변화할 때 $\epsilon$도 함께 조정된다. Yelp2018 이나 Amazon-Book를 살펴볼 때 보다 정교하게 조정할 수 있다고 판단되기 때문에 본 논문에서는 $\lambda$를 고정하고 $\epsilon$을 조정하면서 실험하였으며, 실험 결과는 [Figure 9]와 같다. 실험 결과 $\epsilon$이 0.1인 경우에 가장 성능이 우수한 것으로 확인된다. 이때 Xavier initialization을 쓰는 것이 Gaussian initialzation을 쓸 때보다 3~4% 정도 성능이 개선되었다고 한다.
4.4 Performance Comparison with Other Methods
이전까지는 전부 SimSGL의 성능을 SGL 혹은 LightGCN 만 비교하였다. 4.4 절에서는 다른 SoTA 모델과 비교하여 성능이개선되었는지 확인하였다. 당연히 모든 데이터셋에 대해 SimGCL의 성능이 가장 우수한 것으로 확인된다. MixGCF의 성능도 우수한 것으로 보인다.

4.5 Performance Comparison with Different Types of Noises
본 논문에서는 SimSGL에서 노이즈를 생성할 때 균일분포를 사용하여 구현하였다. 그러나, 노이즈를 생성하는 방법에는 다양한 방법이 존재한다. 4.5 절에서는 노이즈를 생성하기 위해 다양한 분포를 사용하여 실험을 검증하고 어떤 분포의 노이즈일 때 성능이 가장 우수한지 확인하고자 한다. $u$는 U(0,1), 균일 분포를 따는 것을 의미하고 , $p$는 positive 균일 분포, $g$는 가우시안 분포 $a$는 FGSM에 의해서 생성되는 $\text{adversarial noise}$를 의미한다. 실험 결과, SimGCL$_u$와 SimGCL$_g$의 성능이 가장 우수한 것으로 확인된다. 즉, 처음 제안한 균일 분포와 가우시안 분포를 가정하여 노이즈를 생성할 때 가장 우수한 성능을 나타내고 있다.

Conclusion
본 논문에서는 추천 시스템에서 처음 사용된 Dropout 기반 CL을 다시 뜯어보고 추천 성능을 향상시키고자 하는 연구를 진행하였다. 실험 결과, CL 기반 추천 모델에서 Graph Augmentation이 핵심이 아니라, CL Loss가 핵심이라는 것을 확인하였다. 최적화된 CL Loss는 표현 분포를 보다 균일하게 만들고 있으며, 이는 추천 시스템에서 제품 추천에 편향이 생기지 않도록 만들어 준다. 다시 말해, 실제 제품을 추천할 때 많이 구매된 제품 등으로 인해 추천이 편향되는 문제가 존재하지만, CL Loss를 사용하면 추천이 편향되는 문제를 일부 해소할 수있다. 그 다음 직접적인 방식으로 표현 분포의 균일성을 조절하기 위해 노이즈를 사용하는 방법을 적용한 SimSGL을 제안하였다. 실험을 통해 SimSGL이 기존 방법에 비해 성능이 우수하고, 훈련 시간 역시 단축시킬 수 있다는 것을 확인하였다.