Contents
GCMC는 추천 시스템에 그래프를 접목한 연구 중 하나다. auto-encoder framework를 사용하여 link prediction을 수행한다. SoTA 성능까지 달성한 모델로 추천 시스템과 그래프를 접목한 연구 중 널리 알려진 모델이다.
Introduction
논문의 제목에서도 알 수 있듯 Matrix Completion 관점에서 link prediction task를 수행하는 모델이다. 기본적으로 Interaction data는 사용자와 제품 간의 관계로 이루어진 Bipartitle Graph 형태로 구성되어 있다. 본 논문에서는 Bipartitle Graph를 위한 auto-encoder framework인 GC-MC(Graph Convolution Matrix Completion)를 제안한다. 여기서 Matrix Completion은 사용자가 평가하지 않은 제품 혹은 구매하지 않은 제품은 0으로 표현하는데, 이 값을 채운다는 의미다. 즉, 사용자가 구매하지 않은 제품, 평가하지 않은 제품에 대해서 사용자의 구매 확률 혹은 평점을 예측하는 것이다.
Matrix Completion as link prediction in bipartite graphs
먼저 논문에서 사용한 기호에 대해서 알아보자. 평점 행렬은 $M^{ N_u \times N_v}$로 표현하고 여기서 $N_u$는 사용자의 수를 의미하고, $N_v$는 제품의 수를 의미한다. 이때 $M_{ij}$는 사용자와 제품으로 구성된 평점 행렬을 의미한다. 예를 들어, 사용자 $i$가 제품 $j$에 평점 4점을 부여한 경우 $M_{ij}=4$가 되며, 평점을 부여하지 않은 제품에 대해서는 0으로 표기한다.
본 논문에서는 평점 행렬을 입력으로 사용하고 Graph Auto-Encoder를 사용해 축소 후 다시 복원하여 Link prediction을 수행한다.
Graph auto-encoders
본 논문에서는 auto-encoder를 사용하기 때문에 auto-encoder가 일단 먼지부터 알아보자. auto encoder는 encoder model $Z=f(X, A)$와, decoder model $\check{A} = g(Z)$로 구성된다. encoder model은 입력으로 $X \in \mathbb{R}^{N \times D}$와 인접 행렬 $A$를 입력으로 사용하여, $N \times E$ 차원의 node embedding matrix $Z = [z^{\top}_1, ..., z^{\top}_N ]^{\top}$을 출력한다. bipartite graph는 $G = (\mathcal{W}, \mathcal{E}, \mathcal{R}$로 표기한다. 본 논문에서는 rating에 대해서 각각의 점수를 산출하기 때문에 $f(X, M_1, ..., M_R)$로 표기하며 $M_r \in \{0, 1\}^{N_u \times N_v}$가 된다.
Graph Convolutional encoder
본 논문에서는 일반적으로 사용하는 Graph Convolutional Network를 사용한다. GCN은 Message passing과 akwlakr aggregate으로 이루어져 있으며, 아래와 같은 수식으로 표현할 수 있다.
\[ \mu_{j \rightarrow i, r} = \frac{1}{c_{ij}} W_r x_j \]
$c_{ij}$는 normalization 상수를 의미하며 일반적으로는 $\sqrt{|\mathcal{N_i}| |\mathcal{N_j}|}$를 사용한다. $\mathcal{N_i}$는 노드 $i$의 이웃 수를 의미한다. 이때 $\mu_{i \rightarrow j, r}$는 주변 이웃 노드에게 전달 받은 Message를 의미한다.
\[ h_i = \sigma \left [ \text{accum} \left ( \sum_{j \in \mathcal{N}_{i, 1}} \mu_{j \rightarrow i, 1}, ..., \sum_{j \in \mathcal{N}_{i, R}} \mu_{j \rightarrow i, R} \right ) \right ] \]
본 논문에서는 평점 1인 신호와 평점 2 나아가 평점 R 인 신호를 별도로 합산하여 계산한다.
\[ u_i = \sigma (W h_i) \]
최종적으로 Weight Matrix $W$를 곱한 후 활성화 함수를 적용하여 최종 예측 평점을 도출하는 형태로 진행한다.
Bilinear decoder
위 과정을 통해 $U$와 $V$를 생성하였다. 이제는 Bilinear decoder를 통과하여 최종 $\check{M}$을 도출하여야 한다. 이때는 Softmax 함수를 사용하여 각 평점에 대한 확률값을 도출한다.
\[ p(\check{M}_{ij} = r) = \frac{ e^{u_i^{top} Q_r v_j}}{\sum_{s \in R} e^{u^{\top}_i Q_s v_j}} \]
$Q_r \in \mathbb{R}^{E \times E}$는 학습가능한 Weight Matrix를 의미하고, $E$는 사용자와 제품의 hiden size를 의미한다. 위 수식을 통해 각각의 rating에 대한 확률값을 도출한 후 아래의 수식으로 최종 $\check{M}_{ij}$를 생성할 수 있다.
\[ \check{M}_{ij} = g(u_i, v_j) = \mathbb{E}_{p ( \check{M}_{ij} = r )} [r] = \sum_{r \in R} r \ p (\check{M}_{ij} = r) \]
Model training
Loss function은 negative log likelihood를 통해 최소화하는 방향으로 학습할 수 있다.
\[ \mathcal{L} = - \sum_{i, j; \Omega_{ij}=1} \sum_{r=1}^R I [r = M_{ij}] \log p(\check{M}_{ij} = r) \]
$I [k = l] = 1$의 의미는 $k=l$인 경우에는 1을 나타내고 아닌 경우에는 0을 나타낸다. 본 논문에서는 평점 1, 2, 3 등 평점별로 따로 계산하기 때문에 이러한 수식이 나온다. $\Omega \in \{0, 1\} ^{N_u \times N_i}$는 관측되지 않은 rating을 마스킹하는 함수를 의미한다.
본 논문은 Loss function뿐만 아니라 Node dropout, Mini-batching 등을 함께 사용하였으나, 이에 대한 방법은 다른 논문에서도 함께 사용하는 방식이기 때문에 본 글에서는 따로 다루진 않는다.
Vectorized implementation
본 논문에서는 Graph encoder에서 생성한 $U, V$를 Bilinear decoder를 사용하여 평점을 예측하는 형태로 진행한다. 이를 수식으로 표현하면 아래와 같다.
\[ \begin{bmatrix} U \\ V \end{bmatrix} = f(X, M_1, ..., M_R) = \sigma \left ( \begin{bmatrix} H_u \\ H_v \end{bmatrix} W^{\top} \right ), \]
\[ \text{with } \begin{bmatrix} H_u \\ H_v \end{bmatrix} = \sigma \left ( \sum^R_{r=1} D^{-1} \mathcal{M}_r X W^{\top}_r \right ), \]
\[ \text{and } \mathcal{M}_r = \begin{pmatrix} 0 & M_r \\ M^{\top}_r & 0 \end{pmatrix}. \]
Input feature representation and side information
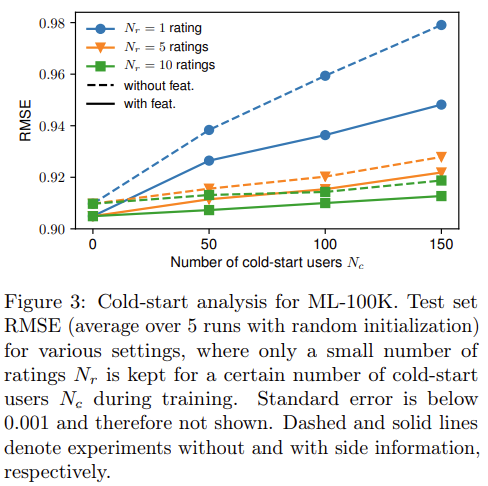
본 논문에서는 side information을 추가하면서 cold start를 해결할 수 있다고 한다. 실제 실험에서는 side information을 사용하지 않았으나, side information을 사용하는 경우 아래와 같은 수식으로 사용할 수 있다.
\[ u_i = \sigma ( Wh_i + W_2^f f_i) \quad \text{with} \quad f_i = \sigma(W_1^f x^f_i + b) \]
이때 $x^f_i$는 노드 $i$에 대한 feature vector를 의미한다. 입력을 할 때 feature vector에 side information을 넣고 사용할 수 있다. $W^f_1$과 $W^f_2$는 학습가능한 Weight Matrix를 의미한다.
Weight Sharing
위에서 계산한 Latent Vector는 Message Passing 을 통해 각 사용자 혹은 제품으로 전달된다. 그러나 각 평점에 대해 동일한 등급을 가질 필요가 없다. 구체적으로 평점 1을 부여한 값과 평점 5를 부여한 값을 동일하게 가질 필요가 없다. 따라서, 아래와 같은 수식을 통해 평점에 따라 가중치를 달리 부여하고 Weight Matrix를 공유한다.
\[ W_r = \sum^r_{s=1} T_s \]
이와 같이 Weight를 공유하여 더 높은 등급의 가중치가 커지는 형태를 Oridinal Weight Sharing이라고 한다.
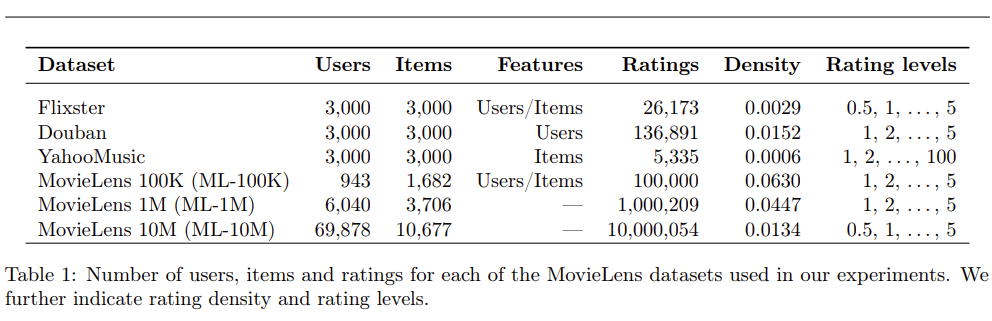
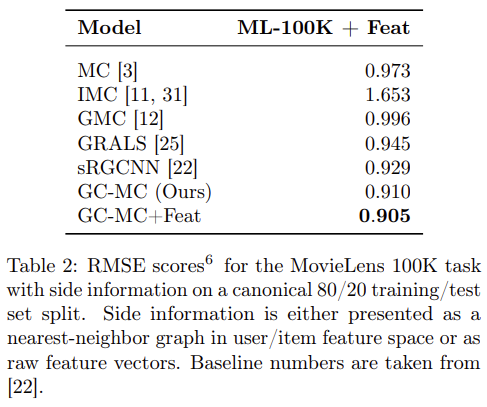
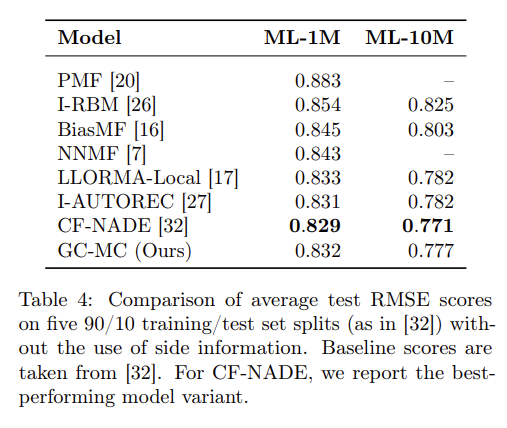
Experiments
실험의 경우 다양한 방법으로 진행하였다. 실험 결과 본 논문에서 제안하는 GC-MC의 성능이 가장 우수한 것을 확인할 수 있으며, Cold-Start analysis에서도 GC-MC의 장점을 확인할수 있다.
