Contents
이번에 리뷰할 논문은 2023년도 AAAI 컨퍼런스 논문인 Dynamic Multi-Behavior Sequence Modeling for Next Item Recommendation이다. 포항공대 연구실과 GS 리테일이 함께 논문을 작성하였으며, GS 리테일을 이용하는 사용자의 정보도 함께 사용하여 성능을 비교분석한 논문으로 매우 흥미로운 논문이다.
논문을 간략하게 설명하면, 본 논문에서 제안하는 Dynamic Multi-behavior Sequence modeling (DyMuS)는 Sequence Recommender Systems (SRSs) 기반으로 사용자가 소비할 다음 제품을 예측하는 기법을 의미한다. 기존에 존재하는 SRSs 기법들은 전부 사용자의 single type에만 초점을 맞추고 있다. 구체적으로, 구매를 하거나(purchase), 클릭(Click), 장바구니(Add-to-cart) 등과 같은 하나의 유형에만 초점을 맞추고 연구를 진행하고 있기 때문에 본 논문에서는 Multi-behavior을 고려하는 기법을 제안하였다. 그리고 향상된 버전인 DyMuS+기법도 함께 제안하였다.
Introduction
사용자는 시간이 지남에 따라 계속해서 선호하는 제품이 달라질 수 있다. 이러한 문제를 고려하기 위해 Sequential Recommender System (SRS) 기법이 제안되었다. 기존 연구에서 제안된 SRS 기법은 대부분 Single Type 에 대해서만 다루고 있으며, Multi-Behavior Sequence를 고려하는 논문은 상대적으로 부족하다. 그러나, 실제 환경에서 사용자들은 구매, 클릭, 장바구니에 담는 등의 다양한 행동을 하기 때문에 Single Type만 고려하게 된다면 추천 성능을 저하시키는 원인이 될수 있다. Single-Behavior 에 비해 Multi-Behavior은 사용자의 관심을 다양한 관점으로 제공하며, 사용자의 관심에 대한 Context와 행동 간의 인과관계를 암시한다.
따라서, 본 논문에서는 먼저 SRS에서 고려해야할 Multi-Behavior Sequence의 특성을 다룬다. 첫 번째, 각 행동 유형의 데이터는 불균형하다. 두 번째, Multi-Behavior Sequence는 사용자의 관심사에 대한 heterogeneous 정보를 제공하므로, 다음 항목을 예측하는 데 있어서 추가적인 정보를 제공할 수 있다. 세 번째, 각 유형의 행동의 순서와 그 중요성에 관련된 정보는 사용자에게 개인화된다. 네 번째, behavior sequence 간의 correlation이 존재한다.
기존의 SRS 기법들은 Single Behavior만 고려하거나 단순히 Multi-Behavior Sequence만 고려하였으며, 위에서 언급한 네 가지의 특성을 다루지는 않았다. 따라서, 본 연구에서는 위에서 언급한 네 가지 특성을 고려하는 DyMuS와 DyMuS+ 기법을 제안하였다. 제안하는 기법은 각 행동과 결합한 행동들을 인코딩(Encoding)하는 방법을 사용한다. DyMuS 기법은 기존 연구에서 제안된 다양한 제품 후보(Candidate) 중에서 결합된 결과에 필요한 중요 정보를 결합하는 Dynamic Routing 기법을 사용하여 각 Behavior Sequence에 대한 인코딩된 정보를 결합한다. DyMuS+ 기법은 각 Behavior Sequence 모델링 단계에 Dynamic Routing을 추가로 적용하여 상관관계를 기반으로 제품의 heterogeneous 정보와 Personalization을 고려한다.
Related Work
본 논문에서는 Sequence Recommender Systems와 Multi-Behavior Recommender Systems 그리고 Dynamic Routing 에 대한 관련 연구를 조사하였으며, 각 파트에 대한 논문은 다음과 같다.
Sequence Recommender Systems: GRU4Rec, SASRec, FMLP-Rec, TGT, MBN.
Multi-Behavior Recommender Systems: HMG-CR, CML, METAS, EHCF.
Dynamic Routing: CapsNet, CARP, JTCN.
MBN: Towards Multi-Behavior Sequence Modeling for Next Basket Recommendation | ACM Transactions on Knowledge Discovery from Data
Next basket recommendation aims at predicting the next set of items that a user would likely purchase together, which plays an important role in e-commerce platforms. Unlike conventional item recommendation, the next basket recommendation focuses on ...
dl.acm.org
Method
DyMuS
DyMuS 기법의 기본 골조는 GRU 기법으로 이루어져 있으며, 이를 통해 Multi-Behavior 간의 상관관계로 부터 Personalized와 Heterogeneous Information를 추출한다. DyMuS+ 기법은 제품 수준의 Heterogeneous와 Personalization을 추출한다. $I$와 $B$는 각각 제품과 행동을 의미한다. 사용자에 대한 행동의 집합은 $S = \bigcup_{b \in B} \{ s_b \} $이며, $s_b = [ i^b_1, i^b_2, ..., i^b_{t_b} ] $를 나타내고, $i^b_k \in I$는 $k$ 번째 제품을 나타낸다. 그런 다음 Sequence $s_b = [i^b_1, ..., i^b_{t_b} ]$를 GRU를 이용하여 아래의 수식과 같이 Representation $e^b$를 생성한다.
\[ \begin{equation} \begin{split} r_k & = \sigma (W^{ir} i^b_k + W^{hr} h_{k-1} + b^r ) \\ \\ z_k & = \sigma (W^{iz} i^b_k + W^{hz} h_{k-1} + b^z) \\ \\ n_k & = \text{tanh} (W^{in} i^b_k + r_k * W^{hn} h_{k-1} + b^n) \\ \\ h_k & = z_k * n_k + (1 - z_k) * h_{k-1} \end{split} \end{equation} \]
$W* \in \mathbb{R}^{D \times D} $는 weight matrices를 의미하고 , $b* \in \mathbb{R}^D$는 bias를 의미한다. $*$는 원소별 곱을 의미하고, $h_k \in \mathbb{R}^D$는 $k$ 번째 hidden state를 의미한다. GRU의 마지막 hidden state인 $h_{t_b}$는 Representation $e^b$를 의미한다.
Dynamic Routing
GRU Layer를 통과한 다음은 Dynamic Routing 단계이다. Dynamic Routing은 input entities에 대한 heterogeneous information을 인코딩하는 여러 후보 capsule 중에서 동적으로 capsule을 통합하는 기법이다. 쉽게 말하자면, Attention Network를 예로 들 수 있다. 반복적으로 가중치를 업데이트하면서 최적의 heterogeneous information을 추출하는 것이다.
\[ u^d_c = W_{dc} \times [ e^1_d \cdots e^{|B|}_d ]^{\top} \in \mathbb{R}^L \]
이때 $u^d_c$는 캡슐을 의미하고, 캡슐은 제품의 수보다 작다. $c$는 캡슐 후보를 의미한다.
\[ c^{(l)}_{dc} = \frac{ \exp(b^{(l)}_{dc}) }{ \sum^C_{c^{\prime}} \exp(b^{(l)}_{dc^{\prime}} )} \]
$b^{(l)}_{dc}$는 상관계수를 의미한다. 그 다음 최종 캡슐 벡터 $v^{(l)}_c$를 도출하게 되며, $v$는 아래와 같이 계산된다.
\[ v^{(l)}_c = \alpha \sum^D_{d=1} c^{(l)}_{dc} u^d_c \in \mathbb{R}^C \]
$l=1, ..., r$은 업데이트의 반복 횟수를 의미한다. 이를 통해 각 캡슐에 대한 벡터가 도출되었으며, 이를 L2 정규화를 사용하여 아래와 같이 최종적으로 벡터를 생성한다.
\[ \begin{equation} \begin{split} \bar{v}^{(l)} & = [ || v^{(l)}_1 ||_2 \quad ||v^{(l)}_2 ||_2 \quad \cdots \quad ||v^{(l)}_C ||_2 ]^{\top} \in \mathbb{R}^C \\ \\ v^{(l)} & = w \cdot \bar{v}^{(l)} + b \in \mathbb{R}^C \end{split} \end{equation} \]
DyMuS+
DyMuS+는 DyMuS와는 달리 제품 수준에서의 heterogeneous, personalization information을 추출한다고 언급했다. 따라서, 아래와 같은 수식으로 계산할 수 있다.
\[ \begin{equation} \begin{split} R^{(l)} & = \sigma (W^{ir} i^b_i * (W^{cr} \otimes C^{(l)}_k + B^{cr}) W^{hr} \otimes H^{(l)}_{(k-1)} + B^r ) \\ \\ Z^{(l)}_k & = \sigma ( W^{iz} i^b_k * ( W^{cz} \otimes C^{(l)}_k + B^{cz} ) + W^{hz} \otimes H^{(l)}_{(k-1)} + B^z ) \\ \\ N^{(l)}_k & = \text{tanh} (W^{in} i^b_k * (W^{cn} \otimes C^{(l)}_k + B^{cn} ) + R^{(l)}_k * (W^{hn} \otimes H^{(l)}_{(k-1)} ) + B^n ) \\ \\ H^{(l)}_k & = Z^{(l)}_k * N^{(l)}_k + (1 - Z^{(l)}_k ) * H^{(l)}_{(k-1)} \end{split} \end{equation} \]
\[ [u^{d(l)}_1 \cdots u^{d(l)}_c \cdots u^{d(l)}_C ] = W_d \otimes [ e^{1(l)}_d \cdots e^{|B|(l)}_d ] \in \mathbb{R}^{L \times C} \]
\[ C^{(l+1)}_k = C^{(l)}_k + N^{(l)}_k * [r^{(l)}_1 \cdots r^{(l)}_C ] \in \mathbb{R}^{D \times C}\]
Prediction
최종 예측 단계는 Cross-Entropy Loss를 사용하며 아래의 수식으로 표현할 수 있다.
\[ L = - \frac{1}{|S^T|} \sum_{S \in S^T} \sum_{i \in I} ( y_{S_i} \log \hat{y}_{S_i} + (1 - y_{S_i} ) \log (1 - \hat{y}_{S_i} ) ) \]
Experiments
실험 단계는 당연히 본 연구에서 제안하는 기법의 성능이 가장 우수한 것을 확인할 수 있다. 본 논문에서는 다른 논문과는 달리 GS 리테일 데이터를 활용하고, 중국 Taobao, Tmall 데이터를 활용하였다. 벤치마크 모델로는 BPR-MF, GRP4Rec, SASRec, FMLP-Rec, METAS, EHCF, HMG-CR, CML, MBN, TGT 등의 기법을 활용하였다.
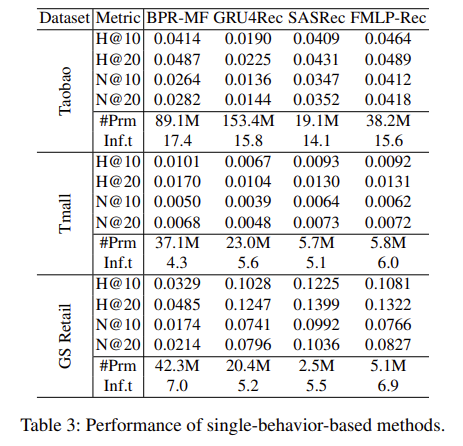
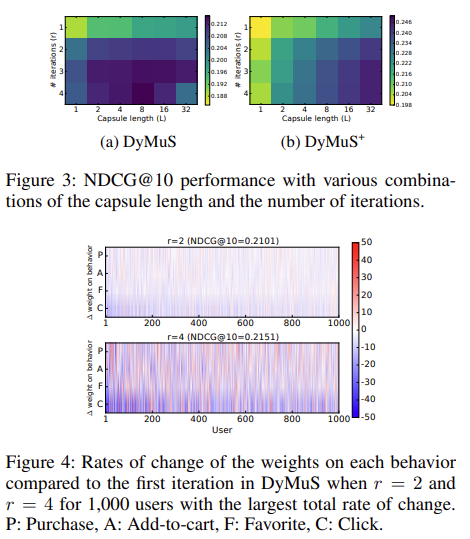
결론으로는, 본 연구에서 제안하는 DyMuS 기법은 마지막 단계에서 Dynamic Routing을 쓰는 것 보다 실제 제품 수준에 적용하는 모델인 DyMuS+ 기법의 성능이 우수한 것을 확인할 수 있다. 그리고 Single Behavior 관련 기법보다는 아주 우수한 성능을 발휘하고 있으며, Multi-Behavior 관련 기법보다도 우수한 성능을 발휘하는 것을 확인할 수 있다.