Contents
Simplifying Graph-based Collaborative Filtering for Recommendation 논문은 WSDM'23 컨퍼런스에서 발표되었다. 기존 추천 시스템에서 성능이 우수한 것으로 알려진 LightGCN에 비해 성능적인 부분이 향상된 것뿐만 아니라, 속도도 매우 빨라진 SGCF를 제안한 논문이다.
Abstract
Graph Convolutional Networks (GCN) 기법은 여러개의 Convolutional 층을 쌓고 비선형 활성화함수를 사용하는 기법으로 머신러닝 분야에서 주로 사용되는 기법이다. 최근 추천 시스템 연구에서도 GCN을 기반으로 한 추천 시스템을 제안하고 있으나, 큰 데이터셋에서 비활성화 함수는 오히려 학습을 어렵게 한다. 또한, GCN 기법의 경우 Layer를 깊게 쌓으면 Over-Smoothing 문제가 발생한다. 본 연구에서는 1) 비선형 함수를 제거하고, 2) 압축된(Condense) 그래프에서 각 노드에 대한 임베딩의 초기치를 얻는 방식으로 성능을 개선하고 Over-Smoothing 문제를 완화하였다. 본 연구에서 제안하는 추천 시스템은 선형 모델이기 때문에 학습하기 쉽고, 큰 데이터셋에서도 Scalable 하다.
Introduction
추천 시스템은 사용자의 정보 과부하 문제를 완화하기 위해 제안되었으며, 사용자의 과거 상호작용(Interaction)을 기반으로 사용자와 제품에 대한 임베딩(Embedding)을 학습하는 기법이다. 최근에는 GCN 기법을 주로 사용하여 추천 시스템을 구축하고 있다. GCN 기반 기법은 사용자와 제품 간의 고차 연결성(Higher-order connectivity)을 고려할 수 있기 때문에 추천 성능을 향상시킬 수 있다. (대표적인 GCN 기반 추천 기법은 PinSage, M2GRL 등이 있다)
최근 연구에서는 성능이 검증된 GCN 기반 기법의 성능을 향상시키기 위해 더 정교하게 모델을 구축하고 있다. 그러나 이와 같은 기법들의 경우 복잡하기 때문에 Large Graph에서 학습하는 것이 어렵고 효율성 및 확장성 문제를 발생시킬 수 있다. 또한, Message Passing 단계에서 연산 시간이 매우 오래걸린다.
본 연구에서는 위 문제를 완화하기 위해 GCN 기법 안에 Feature Transformation과 Nonlinear activation의 필요성과 GCN 기반 추천 시스템의 속도 향상을 다룬다. 이를 위해 GCN Layer 간의 비선형 함수를 제거하고 Resulting Function을 단일 선형 변환으로 축소하여 과도한 복잡성을 감소시킨다. 구체적으로, Large Graph에서 다층 노드 정보를 효율적으로 학습하고 반영하기 위해 Graph Partition-based Algorithm을 고안하였다. (Figure 1)
Preliminaries
2장에서는 해당 논문에서 사용하는 그래프의 기호와 관련 연구에 대해서 간략히 다룬다. $\mathcal{G} = < \mathcal{V}, \boldsymbol{E} >$는 그래프를 의미하고, $\mathcal{V}$는 node, $\boldsymbol{E}$는 edge $e_{ij}$를 의미한다. $\boldsymbol{A}$는 인접 행렬(Adjacency Matrix), $\tilde{L} = \tilde{D}^{-\frac{1}{2}} A \tilde{D}^{-\frac{1}{2}}$는 표준화된 인접행렬을 의미한다. $\tilde{D}$는 차수 행렬(Degree Matrix)을 의미한다.
Graph Convolutional Networks
Graph Convolution Networks (GCN)느 Feature propagation, Feature transformation, nonlinear transition으로 구성되어 있다. 먼저 Feature propagation는 다음 노드로 정보를 전파하는 단계이며 아래와 같은 수식으로 구성 된다.
\[ \bar{H}^{(k+1)} = \tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}} H^k \]
$H$는 k 번째 Layer의 feature를 의미한다. 그 다음으로 Feature transformation과 Nonlinear function은 Weight matrix와 Nonlinear function으로 구성된다.
\[ H^{(k)} = \text{ReLU}(\bar{H}^{(k)} W^{(k)}) \]
Graph Convolutional based Recommendation
그래프 기반 추천 시스템의 경우 Rating matrix $R\in \mathbb{R}^{M \times N}$을 입력으로 사용하며, $M$과 $N$는 각각 사용자의 수와 제품의 수를 의미한다. 추천 시스템에서는 아래와 같이 인접 행렬을 만들어 사용한다.
\[ A = \begin{bmatrix} R & 0^{(N \times M)} \\ \\ 0^{(M \times N)} & R^{\mathbf{T}} \end{bmatrix} \]
$\boldsymbol{E} \in \mathbb{R}^{(M + N) \times D}$는 사용자와 제품의 임베딩 행렬을 의미한다.
Graph Partition Technique
초기 임베딩 행렬의 값을 선정하는 방법 중 가장 간단한 방법은 바로 랜덤으로 임베딩 값을 설정하는 것이다. 그러나, 이와 같은 방식은 그래프 구조를 전혀 반영하지 못한다. 따라서, 본 연구에서는 Graph Partition based Algorithm을 사용하여 분할된 그래프를 통해 입력 그래프를 설명하는 것에 초점을 둔다. $\mathcal{P}$는 분할된 $\mathcal{G}$를 의미하며, k개의 노드를 가진다. $\mathcal{P} = \mathcal{V}_1, \mathcal{V}_2, ..., \mathcal{V}_k$ 이때 k는 사용자가 정하면 된다. 노드 $v \in \mathcal{V}$가 주어졌을 때 $v$가 있는 파티션을 $\mathcal{V}^{\prime} \in \mathcal{P}$라 하고, $p(v) = \mathcal{V}^{\prime}$ 이라고 하자. 이때 동일한 파티션에 있는 노드는 Internal node라고 부르고, 다른 파티션에 있는 노드는 External node라고 부른다. 추가적으로, $v\in \mathcal{V}$가 $p(v) \neq p(n)$ 즉, 다른 파티션에 속하는 노드를 이웃으로 가지는 경우 경계 노드(border node)라고 하며 $\mathcal{V}_b$는 경계 노드의 집합을 나타낸다.
Method
Overall Structure of Our Model
본 논문에서는 위 내용을 바탕으로 Simple Graph convolutional Collaborative Filtering (SGCF) 기법을 제안하였다. SGCF 기법은 기존의 GCN 기반 추천 시스템에서 두 가지 부분을 향상시켰다. 첫 번째, Nonlinear activation function, linear transformation 방식을 사용하지 않고 간단한 선형 전파방식을 사용하여 성능을 개선하였다. 두 번째, 그래프를 여러 개의 작은 Sub-graph로 분할하여 노드의 Internal, External 구조 정보를 포착하여 효율성과 성능을 모두 향상시켰다.
Simplified Embedding Propagation
본 연구에서는 GCN Layer 사이의 Non-linearity가 그다지 중요하지 않을 것이라고 가정하고 Nonlinear transition function을 제거하고 실험을 진행하였다.
\[ E^{0} = E \]
\[ E^{k+1} = SE^kWk\]
$S = \tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}}$를 의미하고, $W^k$는 가중치 행렬을 의미한다. 행렬 형태로 되어 있는 위 수식을 각 사용자와 제품에 대한 수식으로 변환하면 아래와 같다.
\[ \left[E^{k+1}\right]_u = e^{k+1}_u = \left[ \frac{1}{d_u} e^k_u + \sum_{j \in R_u} \frac{1}{d_j \times d_u} e^k_j \right] W^k \]
\[ \left[E^{k+1}\right]_i = e^{k+1}_i = \left[\frac{1}{d_i}e^k_i + \sum_{u \in R_i} \frac{1}{d_i \times d_u} e^k_u \right] W^k \]
Model Prediction with Condensed Graph
위 과정을 수행하면 최종 임베딩인 $E^K$가 도출될 것이다. 추천 시스템에서는 사용자 임베딩 벡터와 제품 임베딩 백터를 내적하여 최종 $\hat{y}$를 예측한다. 이를 수식으로 표현하면 아래와 같다.
\[ \hat{y}_{ui} = < e^K_u, e^K_i > \]
<,> 는 내적 연산을 의미한다.
본 연구에서는 Over-Smoothing 문제를 완화하기 위해 Graph partition technique를 사용한다. Graph partition technique에서는 압축된 그래프를 사용하는데, 압축 그래프는 $\mathcal{G}_c (\mathcal{V}_c, \mathcal{E}_c)$로 표기한다. 본 연구에서는 먼저 $\mathcal{G}$의 partitioning $\mathcal{P} = \mathcal{V}_1, \mathcal{V}_2, ..., \mathcal{V}_k$를 얻는다. Graph Partition의 목적은 $(k, \sigma)$-balanced 하도록 하는 것이며, 아래의 제약을 만족하여야 한다.
\[ \underset{1 \le i \le k}{\text{max}} |\mathcal{V}_i| \le (1 + \sigma) \left[ \frac{|\mathcal{V}|}{k} \right] \]
그리고 edge-cut의 크기를 아래와 같이 최소화하였다.
\[ \underset{1\le i, j \le k}{\bigcup} { (v, u) \in \boldsymbol{E} | v \in \mathcal{V}_i, u \in \mathcal{V}_j} \]
그러나 $(k, \sigma)$-balanced graph partition의 경우 NP-hard 문제이기 때문에 본 연구에서는 GPA algorithm을 사용하여 Graph partitioning을 수행하였다.
남은 문제는 적절한 $k$개를 선정하는 것이다. $k$가 너무 작으면, 효율성을 잃게 되고, $k$가 너무 크면, 압축 그래프의 크기가 너무 커져서 전체적인 계산 비용이 증가하게 된다. 적절한 $k$를 설정하기 위해 본 연구에서는 $k= \lceil \sqrt{\mathcal{V}} \rceil $ 또한, Over-Smoothing 문제를 해결하기 위해 다음과 같은 방식으로 $\hat{y}_{ui}$를 계산하였다.
\[ \begin{equation} \begin{split} \hat{y}_{ui} & = \hat{y}^{k-1}_{ui} + < e^k_u, e^k_i > \\ \\ & = \hat{y}^{k-2}_{ui} + <e^{k-1}_u, e^{k-1}_i > + < e^k_u, e^k_i > \\ \\ & = \hat{y}^0_{ui} + < e^1_u, e^1_i> + \cdots + < e^k_u, e^k_i > \end{split} \end{equation} \]
Model Learning
모델 학습의 경우 추천 시스템에서 널리 사용되는 BPR Loss를 사용하였다.
\[ \min L(R, \hat{R}) = \sum^M_{a=1} \sum_{(i,j)\in D_a} - \ln (s(\hat{r}_{ai} - \hat{r}_{aj} )) + \lambda ||W||^2 \]
Experiments
실험의 경우 Yelp2018, Amazon-Books, Gowalla, MovieLens 와 같은 오픈 데이터를 활용하여 실험하였으며, 베이스라인으로는 MF-Based (MF, ENMF, EATNN, CML), Networking embedding method (DeepWalk, Node2Vec), GCN-Based methods (NGCF, NIA-GCN, LR-GCCF, LightGCN, DGCF)를 사용하였다.
실험 결과를 보면, Amazon-Books 데이터에서는 최대 10% 가량 성능이 개선된 것을 확인할 수 있다.
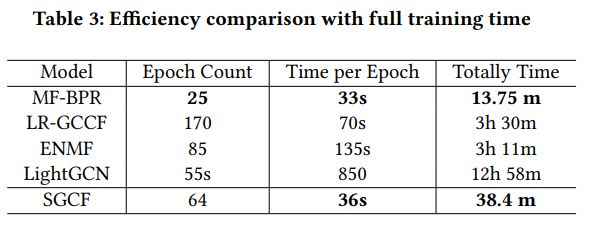
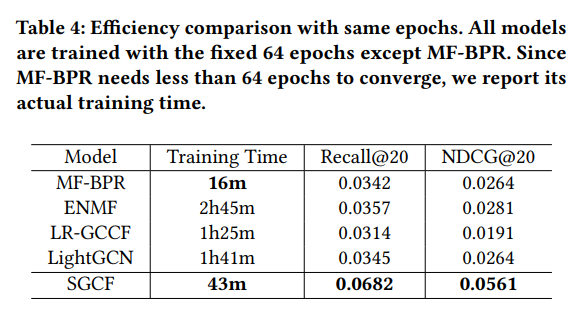
주목할만한 결과로는 SGCF 기법의 속도가 MF-BPR 을 제외한 다른 기법에 비해 매우 우수한 것을 확인할 수 있다. SGCF 기법의 경우 그래프 기반 기법임에도 불구하고 MF 기반 기법과 비슷한 수준의 속도를 보여준다. Table 4를 보면, 빠른 속도 뿐만 아니라 성능 역시 우수한 것을 확인할 수 있다.
