Self-Attentive Sequential Recommendation (ICDM'18)

Contents

• Introduction
• Methodology
  • Embedding Layer
  • Self-Attention Block 
  • Stacking Self-Attention Blocks 
  • Prediction Layer 

 

 

해당 논문은 Sequential Recommendation 논문에서 유명한 모델 중 하나인 SASRec을 제안한 논문이다. Self-Attention 기법을 사용하여 다음 사용자가 행동(Action)할 제품을 예측하는 기법이다. 기존 연구에서 주로 사용하는 Markov Chain (MC)의 경우 이전 제품 혹은 과거 몇 번의 행동을 바탕으로 다음 행동할 제품을 예측하고, RNN의 경우 장기 정보를 고려할 수 있다. 일반적으로 MC는 주로 Sparse한 데이터에서 우수한 성능을 보이고, RNN의 경우 Dense한 데이터에서 우수한 성능을 보이고 있다. 본 연구에서는 Self-Attention Networks를 이용하여 Sparse, Dense와 상관없이 우수한 성능을 발휘하는 SASRec을 제안하였다. 

 

Introduction

예전에는 MC, RNN을 바탕으로 한 Sequential Recommendation이 주를 이루었다. 최근에 Sequential 분야에서는 Transformer가 매우 성능이 우수한 것으로 각광받고 있다. Transformer는 'Self-Attention' 개념을 도입하였으며, Attention은 단어 사이의 관계를 파악하는 것에 있어서 매우 효율적이고 성능 역시 우수하다. 본 연구에서는 최근 각광받는 기술인 Transformer의 Self-Attention 메커니즘을 활용한 SASRec 기법을 제안한다. 

 

Methodology

해당 논문은 Methodology가 중요한 부분이기 때문에 해당 부분에 초점을 맞추어 리뷰하였다. 본 연구에서는 Action Sequence는 $S^u=(S_1^u,S_2^u,\cdots ,S_{|S^u|}^u)$로 정의하였고, 다음 제품을 예측하는 것을 다룬다. 학습할 때 모델은 $t$ 시점의 제품에 의존하여 $t+1$ 시점의 제품을 예측하는 것이다.

 

Embedding Layer

본 연구에서는 $n$으로 최대 Sequence 길이를 제한둔다. 만약 Sequence 길이가 $n$보다 작은 경우에는 Padding을 한다.  Transformer의 경우 Word Embedding과 Position Embedding을 함께 더해서 사용한다. Recommendation에서는 Word Embedding 대신 Item Embedding을 사용하기 때문에 두 Embedding Vector를 더하면 아래와 같은 수식으로 표현할 수 있다. 

$$\hat{E}=\left[\begin{array}{c}\begin{array}{r}{M}_{s_1}+P_1\\ M_{s_2}+P_2\\ \cdots \\ M_{s_n}+P_n\end{array}\end{array}\right]$$

 

Self-Attention Block 

Scaled Dot-Product를 사용하며, 일반적인 내적과 다른 점은 차원에 Sqrt를 해준다는 것이다.

$$\text{Attention}(Q,K,V)=\text{softmax}\left(\frac{Q{K}^{\mathrm{\top }}}{\sqrt{d}}\right)V$$

$Q,K,V$는 각각 쿼리(Query), 키(Key), 벨류(Value)를 의미한다. Self-Attention의 경우 각 단어의 Q, K, V를 사용하여 계산하기 때문에 아래와 같은 수식으로 표현할 수 있다.

$$S=SA(\hat{E})=\text{Attention}(\hat{E}{W}^Q,\hat{E}{W}^K,\hat{E}{W}^V)$$

위 과정을 통해 출력된 값을 바탕으로 Point-Wise Feed Forward Network를 구성하면 된다. 그러나 위 과정은 단순히 Weight Matrix를 곱하는 과정이기 때문에 Linear하다. 따라서, Poin-Wse Feed Forward Network에서는 비선형 함수를 사용하고 다른 잠재 차원 간의 상호작용을 고려하기 위해 아래와 같은 수식을 사용하였다. 

$$F_i=FFN(S_i)=\text{ReLU}(S_i{W}^{(1)}+b^{(1)})W^{(2)}+b^{(2)}$$

이때는 Figure 1에서 보이듯, $S_i$과 $S_j$ 간의 어떠한 상호작용도 존재하지 않는다. ($i\ne j$)

 

Stacking Self-Attention Blocks 

위에서 구축한 Self-Attention Block을 쌓는 단계다. $F_i$는 이전 제품의 임베딩 벡터를 모두 집계한 것을 의미한다. (${\hat{E}}_j,j\le i$). 

$$S^{(b)}=\text{SA}(F^{(b-1)}$$

$$F_i^{(b)}=\text{FFN}(S_i^{(b)}),\mathrm{\forall }i\in 1,2,\cdots ,n$$

그러나 단순히 Self-Attention Block을 여러번 쌓을 경우 1) Overffitting 문제가 발생할 수 있으며, 2) Gradient Vanishing 과 같은 문제가 발생할 수 있고, 3) 층을 여러 겹 쌓기 때문에 파라미터의 수가 너무 많아진다. 이와 같은 문제를 해결하기 위해 Skip Connection, LayerNorm, Dropout 방식을 적용하였다.

$$g^{\prime }=x+\text{Dropout}(g(\text{LayerNorm}(x))$$

$$\text{LayerNorm}(x)=\alpha \odot \frac{x-\mu }{\sqrt{{\sigma }^2+ϵ}}+\beta$$

 

Prediction Layer 

추천 시스템에서는 최종적으로 MF 방식을 활용하여 다음 제품을 추천한다. 

$$r_{i,t}=F_t^{(b)}{N}_i^{\mathrm{\top }}$$

$r_{i,t}$는 $t$ 시점에 제품 $i$의 관련성을 의미한다. $N\in {\mathbb{R}}^{|\mathcal{I}|\times d}$는 제품 임베딩 행렬을 의미한다. 높은 $r_{i,t}$를 가지는 제품을 바탕으로 다음 제품을 예측할 수 있다. 만약 Seqeunce가 Padding되어 있으면 출력값은 <PAD>가 나오고, $1\le t<n$인 경우에는 $s_{t+1}$, 즉 다음 시점의 제품을 예측하고, $t=n$인 경우에는 $S_{|S^u|}^u$를 출력한다. 마지막으로 모델 학습 단계에서는 Binary Cross Entropy Loss를 사용하였으며, SGD를 사용하여 최적화하였다. 

 

 

Experiments

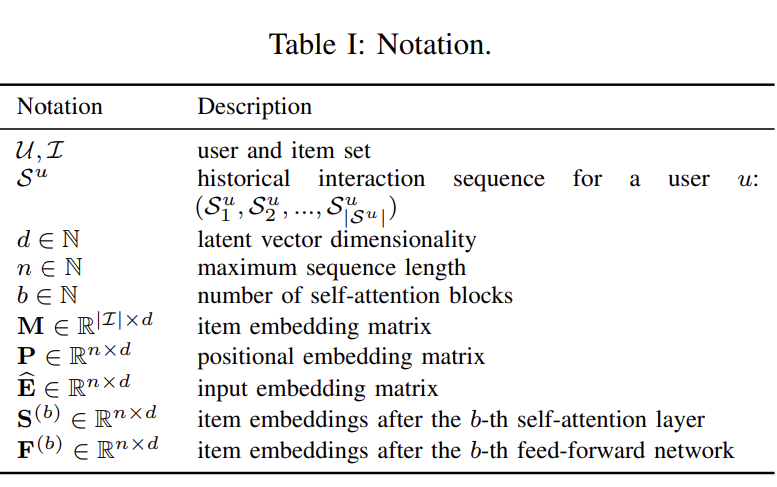
본 연구에서는 총 4가지의 연구 질문(Research Question)을 해결하고자 실험을 진행하였다. 1) SASRec 이 기존 SoTA 모델보다 성능이 좋은가? 2) SASRec의 다양한 Components가 영향을 주는가?(Ablation Study) 3) SASRec이 학습에서 효율적인가? 4) Position, Item 에 대해서 attention weight가 유의미한 패턴을 학습할 수 있는가?

 

RQ1. 에 대해서는 모든 경우에 성능이 우수한 것으로 확인되었다. 

 

 

RQ2. 에 대해서는 다양한 실험을 하였다. PE(Positioinal Embedding), IE(Item Embedding), RC(Residual Connections) 등을 수행했을 때 Attention Block을 1과 3으로 설정했을 때, 혹은 PE를 제거했을 때 성능이 좋아지는 경우가 발생한다. Beauty에서는 조금 신기하게 Position Embedding 즉, 제품의 순서를 고려하지 않았을 때 오히려 좋은 성능을 보이는데, 이를 생각해보면 화장품과 같은 경우는 게임이나 영화 등과 같은 도메인에 비해 제품의 순서가 크게 중요하지 않다는 것을 의미할 수 있다. 

 

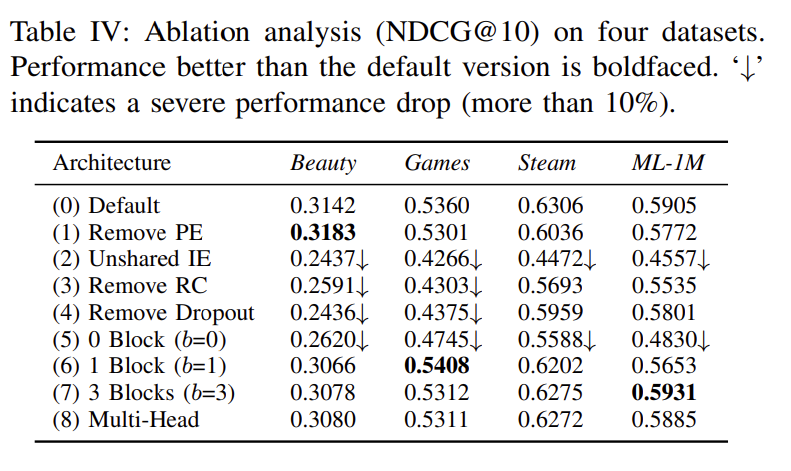
RQ3. 에 대해서는 SASRec이 더 적은 시간에 더 빨리 수렴하는 것뿐만 아니라, NDCG 성능 자체도 훨씬 더 우수한 것을 확인할 수 있다. 

 

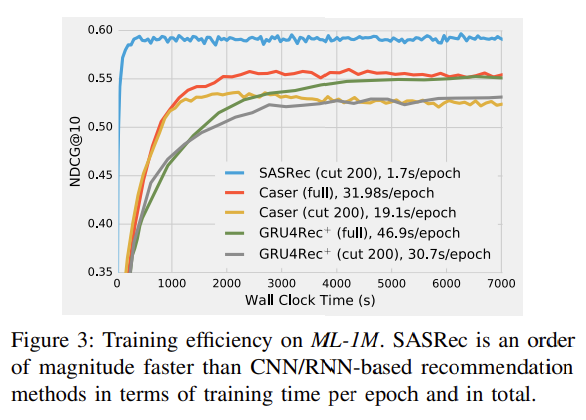
RQ4.에 대해서는 제품에 따라, 즉, 도메인에 따라 Attention Weight의 패턴이 존재하는 것을 볼 수 있다. Position Embedding을 뺏을 때(b)와 빼지 않았을 때(c)와 비교하면 확연히 Attention Weight의 차이가 존재하는 것을 볼 수 있다. (a)와 (c)를 비교하면, Beauty 데이터셋이 ML 데이터셋에 비해 매우 Sparse한데, 데이터가 Sparse한 경우에는 최근 제품에 Attention Weight가 큰 것을 볼 수 있다.