Contents
LightGCL은 추천 시스템에 그래프와 대조 학습(Contrastive Learning)을 도입한 기법이다. 기존 연구에서 주로 사용하는 대조 학습 방식은 node dropout, edge dropout과 같은 확률적 증강(Stochastic Augmentation) 기법을 사용하거나, 휴리스틱 기반 증강(Heuristic-based Augmentation) 기법을 사용하고 있다. 그러나 이와 같은 방식은 노이즈로 인한 편향(Bias)이 존재하기 때문에 원래 그래프의 의미론적인 구조를 제대로 파악하지 못한다. 이와 같은 문제를 해결하고자 본 연구에서는 간단하지만 효과적이고 강건(Robust)한 기법인 LightGCL 기법을 제안하였다.
Introduction
추천 시스템에서 사용되는 GNN 기법은 고차 연결성(High-Order Connectivity)을 고려하기 위해 Message Passing Layer을 여러겹 쌓아 노드(Node)에 대한 임베딩을 학습한다. 그러나 GNN 기반 추천 시스템의 경우 사용자와 제품 간의 상호작용(interaction)이 적어서 발생하는 희소성(Sparsity) 문제에 시달리고 있다. 이와 같은 문제를 해결하기 위해 대조 학습(Contrastive Learning) 기법을 도입하였다. 대조 학습을 사용하는 연구는 대부분 Heuristic-based Contrastive View를 통해서 학습한다. 구체적으로, Positive View와 Negative View를 이용해 두 View에서 구한 상호 정보량(Mutual Information)을 극대화 하는 방향으로 학습하거나 노드의 Semantic 이웃을 식별하여 사용하는 방법이 있다. 대표적인 기법으로는 SGL(Self-supervised Graph Learning), SimGCL(Simple Graph Contrastive Learning), NCL(Neighborhood-enriched Contrastive Learning) 등의 기법이 있다. 그러나 대조 학습을 활용한 추천 시스템 방법 역시 다음과 같은 문제점이 존재한다.
- 무작위로 새로운 View를 만들기 때문에 구조적인 정보를 제대로 얻을 수 없다.
- Heuristic-based 방법의 경우 일반화 성능이 저하될 수 있으며, Noise에 취약하다.
- Over-smoothing 문제가 존재한다.
본 연구에서는 위와 같은 문제를 해결하기 위해 SVD(Singular Value Decomposition)를 기반으로 한 Data Augmentation 방법을 제안한다. SVD 기법을 사용하면, 사용자와 제품 간의 상호작용에서 유용한 정보를 추출할 수 있는 것뿐만 아니라, Global Collaborative Context를 대조 학습에 주입(Inject)시킬 수 있다.
Methodology
LightGCL 기법의 구조는 Figure.1에서 확인할 수 있다. 그림의 윗 부분은 Local Graph Dependency를 추출하고, SVD를 이용한 방법에서는 Global Collaborative relation을 분석하여 대조 학습의 성능을 향상시킨다.

Local Graph Dependency Modeling
먼저 본 연구에서는 $u_i$, $v_j$를 각각 사용자와 제품에 대한 노드로 사용하고, $e^{(u)}_i, e^{(v)}_j \in \mathbb{R}^d$의 차원을 가진다. $d$는 Embedding Dimension Size를 의미한다. 이를 행렬 형태로 변환하면 $E^{(u)} \in \mathbb{R}^{I \times d}, E^{(v)} \in \mathbb{R}^{J \times d}$로 표기하고, $I, J$는 각각 사용자와 제품의 수를 의미한다. 본 연구에서는 기존 선행 연구를 참고하여 $l=2$로 설정한 GCN을 사용하였으며, $l$은 GCN Layer의 수를 의미한다.
\[ z^{(u)}_{i, l} = \sigma ( p(\tilde{A}_{i, :}) \cdot E^{(v)}_{l-1} ), \quad z^{(v)}_{j, l} = \sigma (p(\tilde{A}_{:, j}) \cdot E^{(u)}_{l-1} ) \]
$z^{(u)}_{i, l}, z^{(v)}_{j, l}$는 각각 $l$번째 Layer의 $u_i$와 $v_j$의 Embedding을 의미한다. $\sigma(\cdot)$는 LeakyReLU를 의미하고, $p(\cdot)$는 Over-fitting 문제를 완화하기 위해 사용하는 Edge Dropout을 의미한다. 마지막으로 $\tilde{A}$는 정규화한 인접행렬을 의미한다. 본 연구에서는 추가적으로 Original Infromation을 유지하기 위해 Residual Connection을 추가로 사용하였으며, 수식은 아래와 같이 표현할 수 있다.
\[ e^{(u)}_{i, l} = z^{(u)}_{i, l} + e^{(u)}_{i, l-1}, \quad e^{(v)}_{j, l} = z^{(v)}_{j, l} + e^{(u)}_{j, l-1} \]
최종적으로 모든 Layer의 Embedding을 합계하여 최종 Embedding을 도출한다. 이렇게 도출된 사용자와 제품에 대한 최종 Embedding Vector를 내적(inner-Product)하여 확률을 도출한다.
\[ e^{(u)}_i = \sum^L_{l=0} e^{(u)}_{i, l}, \quad e^{(v)}_j = \sum^L_{l=0} e^{(v)}_{j, l} \]
\[ \hat{y}_{i, j} = e^{(u) \top}_i e^{(v)}_j \]
Efficient Global Collaborative Relation Learning
이번 단계에서는 대조 학습이 Global Structure Learning을 할 수 있도록 하기 위해, SVD 방법을 적용한다. 이를 위해 인접 행렬은 $A = U S V^{\top}$으로 표현하고, $U$와 $V$는 $I \times I$, $J \times J$ 짜리 orthonormal matrix로 구성한다. 이때 $S$는 $I \times J$ matrix가 된다. 본 연구에서는 SVD는 Truncate 하여 차원을 축소해 사용하며 $\hat{A}= U_q S_q V^{\top}_q$, $U_q \in \mathbb{R}^{I \times q}$, $V_q \in \mathbb{R}^{J \times q}$로 사용한다. 이때 q는 singular value가 높은 순으로 q개가 된다. 재구성된 인접 행렬 $\hat{A}$는 원래의 인접 행렬 $A$에 대한 low-rank approximation이 될 것이고, $rank(\hat{A}) = q$가 될 것이다. 이는, 사용자의 선호도 표현에서 중요하고 신뢰할 수 있는 사용자와 제품 간의 상호작용을 식별하는 주성분(Principla components)가 되고, 새로운 그래프 구조의 Global Collaborative Signla을 보존할 수 있다.
\[ g^{(u)}_{i, l} = \sigma ( \hat{A}_{i, :} \cdot E^{(v)}_{l-1}), \quad \sigma ( \hat{A}_{:. j} \cdot E^{(u)}_{l-1} ) \]
그러나 위 과정을 통해 추출된 SVD의 경우 데이터가 많으면 계산 비용이 많아진다. 따라서 본 연구에서는 Randomized SVD 방식을 사용한다.
\[ \hat{U}_q, \hat{S}_q, \hat{V}^{\top}_q = \text{ApproxSVD}(A, q), \quad \hat{A}_{SVD} = \hat{U}_q \hat{S}_q \hat{V}^{\top}_q \]
\[ G^{(u)}_l = \sigma (\hat{A}_{SVD} E^{(v)}_{l-1}) = \sigma (\hat{U}_q \hat{S}_q \hat{V}^{\top}_q E^{(v)}_{l-1}), \quad G^{(v)}_l = \sigma ( \hat{A}^{\top}_{SVD} E^{(u)}_{l-1}) = \sigma ( \hat{V}_q \hat{S}_q \hat{U}^{\top}_q E^{(u)}_{l-1}) \]
$G^{(u)}_l$과 $G^{(v)}_l$는 새롭게 생성된 Graph Structure View의 Embedding 집합을 의미한다. 이와 같이 변환한다면, Dense Matrix인 $\hat{A}$를 저장하지 않고, 상대적으로 용량이 적은 $\hat{U}, \hat{V}, \hat{S}$로 나누어 저장할 수 있기 때문에 효율적이다.
Simplified Local-Global Contrastive Learning
SGL, SimGCL과 같은 Graph Contrastive Learning의 경우 두 개의 View를 생성하여 대조하는 방식을 사용한다. 이때 원본 그래프 구조 (Main View)에서 생성된 Node Embedding은 InfoNCE Loss에 사용되지 않는다. 일반적으로 Recommendation Loss와 Contrastive Learning Loss 를 따로 두고, Hyper-parameters를 통해 Contrastive Learning의 비중을 조절하는 방식이기 때문이다. 그러나 본 연구에서 제안하는 방식은 Main View도 대조 학습에 사용하기 때문에 아래와 같이 Loss Function을 정의할 수 있다.
\[ \mathcal{L}^{(u)}_s = \sum^I_{i=0} \sum^L_{l=0} -\log \frac{\exp(s(z^{(u)}_{i, l}, g^{(u)}_{i, l} )/ \tau ) }{ \sum^I_{i \prime = 0} \exp ( s( z^{(u)}_{i, l}, g^{(u)}_{i \prime, l} ) / \tau ) } \]
이때 Over-fitting을 방지하기 위해 Random Node Dropout 방식을 사용한다.
\[ \mathcal{L} = \mathcal{L}_r + \lambda_1 \cdot ( \mathcal{L}^{(u)}_s + \mathcal{L}^{(v)}_s ) + \lambda_2 \cdot ||\Theta||^2_2, \quad \mathcal{L}_r = \sum^I_{i=0} \sum^S_{s=1} \max( 0, 1 - \hat{y}_{i, p_s} + \hat{y}_{i, n_s}) \]
Evaluation
LightGCL의 성능을 검증하기 위해 총 5개의 연구 질문(Research Question, RQ)을 제시하고, 각 연구질문에 맞추어 실험을 진행한다.
- 기존의 SOTA 모델과 비교했을 때 LightGCL의 성능이 우수한가? - Performance Validation
- 경량화된 대조 학습 방식이 모델의 효율을 향상시키는가? - Efficiency Study (Time Complexity)
- Data Sparsity, Popularity Bias, Over-Smoothing에 대해서 성능이 어떻게 측정되는가?
- Local-Global Contrastive Learning이 모델의 성능에 기여하는가? - Ablation Study, Case Study
- Parameter를 다양하게 설정하였을 때 성능이 어떻게 변하는가? - Case Study (Model Sensitivity)
RQ1) Performance Validation
Contrastive Learning을 사용하는 모델이 사용하지 않는 모델보다 우수한 성능을 보이는 것을 확인할 수 있으며, Contrastive Learning을 사용하는 기법 중에서도 본 연구에서 제안하는 LightGCL의 성능이 가장 우수한 것을 확인할 수 있다. p-value를 통해서 통계적으로도 유의미하게 성능이 향상되었다는 것을 판단할 수 있다.

RQ2) Efficiency Study
본 연구에서는 기존 연구와는 달리 두 가지의 새로운 View를 생성하는 것이 아니라, SVD를 통해 하나의 View만 생성하여 Contrastive Learning을 진행한다. 그렇기 때문에 Contrastive Learning을 사용하지 않는 LightGCN에 비해 시간 복잡도는 높게 측정되지만, SGL, SimGCL 등과 같은 Contrastive Learning에 비해서는 많이 줄어든 것을 확인할 수 있다. 그러나, SVD의 사용자 행렬, 제품 행렬, 대각 행렬에 대한 값을 저장하여야 한다는 단점이 있다.

RQ3) Popular Bias, Data Sparsity, Over-smoothing
Figure 2, 3의 경우는 Popular Bias와 Data Sparsity에 대한 그림이다. X축은 Data Sparsity에 대한 값이며 Interaction의 수가 15 미만인 경우(0 - 15)에 Gowalla 데이터에서 성능이 가장 우수한 것을 확인할 수 있다. 본 연구에서 제안하는 LightGCL 기법의 성능이 우수한 것을 보여준다.

그 다음으로는 Over-Smoothing 문제에 대해서 다루어 본다. MAD는 평균적으로 얼마나 노드들이 떨어져 있는지에 대한 것을 지표화한 것이며, 값이 높을수록 노드 임베딩이 골고루 퍼져있다는 것을 의미한다.


Contrastive Learning이 아닌 기법인 MHCN, LightGCN의 경우 Over-Smoothing 현상이 발생해 노드 임베딩이 대부분 뭉쳐있는 현상을 띄고 있다. 반면에, Contrastive Learning을 사용하는 기법의 경우 1) Over-Uniform 되어 Collaborative Relation을 제대로 파악하지 못하고 2) Clustering된 부분이 너무 작은 Cluster로 구성되어 있으며, Cluster 내부에서는 심한 Over-smoothing 현상이 발생한다.
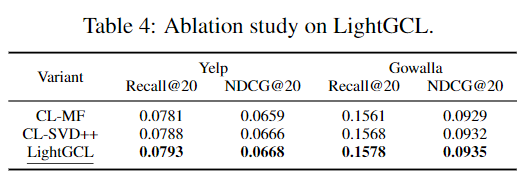
RQ4) Ablation Study and Case Study
RQ4)에서는 SVD가 정말로 성능에 기여하는지 확인하고자 한다. 이를 위해 SVD 외 MF, SVD++과 같은 기법과 비교하였다.
아래의 그림은 $u_{26}$에 대한 예시를 가지고 온 것이다. 실제 사용자는 Cleveland에 살 것으로 추정하고, Arizona를 여행간 것으로 추정할 수 있다. 초록색 박스는 실제 상호작용이 있는 것을 의미하고, 파란색 박스는 상호작용이 없는 것을 의미한다. 사용자는 일반적으로 여행을 갈 때 Car Rent를 이용하면 다른 Car Rent를 사용하지 않는다. 반면에, 호텔의 경우 Arizona에서 호텔을 더 이용할 수 있기 때문에 Test set에 새로운 Arizona Hotel이 추천된 것을 확인할 수 있다. SVD의 Weight를 보면 Car Rent의 Weight가 음수로 매우 작은 값을 가지기 때문에 일반적인 상식에 부합하는 결과가 도출된 것을 확인할 수 있다. SVD의 Weight를 보면 Arizona의 제품에 대해서는 낮은 Weight를 보이고 있으나, Cleveland의 Bar, Restaurant에는 Weight가 높게 나오는 것을 확인할 수 있다.

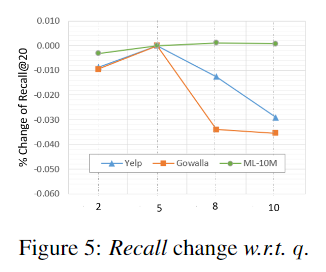
RQ5) Hyperparameter Analysis
본 연구에서는 InfoNCE Loss $\lambda_1$, Temperature $\tau$, Rank of SVD $q$를 하이퍼파라미터로 사용한다. RQ5)에서는 각 하이퍼파라미터를 달리 설정하여 성능 차이가 존재하는지 확인하고자 한다.