Contents
BERT4Rec은 모델명 그대로 BERT를 이용한 Recommendation 모델이다. Sequential 데이터를 다룰 때 주로 사용하는 기법으로, SASRec 다음으로 나온 모델이라고 볼 수 있다. SASRec과 다른 점은 Bidirectional 하다는 점과 Masking 기법을 사용한다는 점이다.
Introduction
기존 Sequence 데이터를 다루는 추천 시스템 연구에서는 주로 Recurrent Neural Network (RNN) 과 같은 기법을 사용하여 Encoding한다. 그러나 RNN 기법은 왼쪽에서 오른쪽으로, 즉, 입력으로 들어오는 제품의 순서만을 고려하기 때문에 left-to-right 방식(Undirectional)은 사용자의 표현(Representation)을 제대로 학습하는 것이 어렵다. 구체적으로, left-to-right 방식은 오로지 이전 제품에 대한 정보만을 고려하기 때문에 Sequence에 잠재된 정보를 제대로 파악하지 못한다. 뿐만 아니라 실제 Sequence에는 노이즈가 있을 수 있는데, 이전 클릭 혹은 구매한 제품에 기반하여 다음 클릭 혹은 구매할 제품을 예측하고 있다.
본 연구에서는 이와 같은 문제를 다루기 위해 Bidirectional 기법인 BERT를 사용하고자 한다. 그러나 단순히 Bidirectional 기법을 사용하게 된다면, $i_2$를 예측할 때 다음에 구매한 제품의 정보까지 알기 때문에 이는 매우 Trivial Solution이 될 수 있다. 따라서, 추가적으로 [MASK]라는 Special Token을 사용하여 무작위로 제품을 Masking하여 사용한다.

BERT4Rec
논문에서 사용하는 기호는 다음과 같다. $\mathcal{U} = {u_1, u_2, \cdots, u_{|\mathcal{U}|} } $와 $\mathcal{V} = { v_1, v_2, \cdots, v_{|\mathcal{V}|} } $ 는 각각 사용자와 제품 집합을 의미한다. $\mathcal{S}_u = [ v^{(u)}_1, \cdots, v^{(u)}_t, \cdots, v^{(u)}_{n_u} ]$는 사용자 $u$에 대한 Sequence를 의미하며, 시간 순서로 정렬하였다( $u \in \mathcal{U}, v^{(u)}_t \in \mathcal{V}$). $t$는 Time Step을 의미하고, $n_u$는 전체 Sequence의 길이를 의미한다. $\mathcal{S}_u$가 주어졌을 때, $n_u + 1$ Time step에 제품을 구매할 확률은 아래와 같이 표현한다.
\[ p(v^{(u)}_{n_u + 1} = v | \mathcal{S}_u )\]
Model Architecture
BERT4Rec의 구조는 Figure 1(b)와 같다. Embedding Layer에서는 Position Embedding과 Item Embedding을 더한 값을 사용하고 나온 출력값을 L개의 Transformer Layer를 통과시켜 $h^L_{t+1}$을 예측하는 형태다. Transformer Layer는 Multi-Head Attention, Dropout, Normalization, Position-wise Feed-Forward로 구성되어 있다.
Transformer Layer
Figure 1(b)에 나오는 $h^l_i$는 $l$번째 Layer의 $i$번째 Hidden Representation을 의미한다. 각 Position의 Hidden Representation을 쌓아서 행렬 형태로 변환하면 $H^l \in \mathbb{R}^{(t \times d)}$가 되며, 이를 Transformer Layer의 입력으로 사용한다.
\[ \text{MH}(H^l) = [\text{head}_1; \text{head}_2; \cdots ; \text{head}_h ] W^O \]
\[ \text{head}_i = \text{Attention} (H^l W^Q_i, H^l W^K_i, H^l W^K_i ) \]
$h$는 Head의 수를 의미하고, $W^Q_i \in \mathbb{R}^{d \times d / h }$, $W^K_i \in \mathbb{R}^{d \times d / h}$, $W^V_i \in \mathbb{R}^{(d \times d / h)}$, $W^O_i \in \mathbb{R}^{d \times d} $는 학습가능한 가중치 행렬을 의미한다. Attention Function은 Scaled Dot-Product Attention을 사용하며, Scaled라는 이름이 붙은 이유는 $\sqrt{d/h}$로 나누어 주기 때문이다.
\[ \text{Attention}(Q, K, V) = \text{softmax} \left( \frac{QK^{\top}}{\sqrt{d/h}} \right ) V \]
$Q, K, V$는 각각 Query, Key, Value를 의미한다. 그다음으로는 Position-wise Fedd-Forward Network가 있으며, 이때는 각각에서 나온 값을 Non-Linear + GELU를 사용하여 계산한다.
\[ \text{PFFN}(H^l) = [\text{FFN}(h^l_1)^{\top}; \cdots ; \text{FFN} (h^l_t)^{\top} ]^{\top} \]
\[ \text{FFN}(x) = \text{GELU}(xW^{(1)} + b^{(1)} ) W^{(2)} + b^{(2)} \]
\[ \text{GELU}(x) = x \Phi (x) \]
$\Phi(x)$는 Cumulative Distribution Function을 의미한다. $W^{(1)} \in \mathbb{R}^{d \times 4d}$, $W^{(2)} \in \mathbb{R}^{4d \times d}$, $b^{(1)} \in \mathbb{R}^{4d} $, $b^{(2)} \in \mathbb{R}^d $는 각각 학습 가능한 가중치 행렬과 편향 벡터들을 의미한다.
마지막으로, 위 단계에서 구축한 Transfomer Layer를 쌓아야 하며, 이는 아래의 식과 같이 나타낼 수 있다.
\[ H^l = \text{Trm} (H^{l-1}), \quad \forall i \in [1, \cdots , L ] \]
\[ \text{Trm}(H^{l-1}) = \text{LN} (A^{l-1} + \text{Dropout}(\text{PFFN}(A^{l-1}))) \]
\[ A^{l-1} = \text{LN}(H^{l-1} + \text{Dropout} ( \text{MH}(H^{l-1} ))) \]
Embedding Layer
Embedding Layer는 비교적 간단하게 계산된다. 기본적으로, Item Embedding이 들어가고, 위치를 파악하기 위한 Position Embedding이 들어간다. 두 값을 단순히 더해서 0번째 Hidden Representation으로 사용한다.
\[ h^0_i = v_i + p_i \]
이때 입력 Seuqence의 길이를 제한하여 사용하는데, 뒤에서 N개의 아이템을 가지고와서 사용한다. 구체적으로, Sequence $[v_1, \cdots, v_t]$가 주어진다면, $[v^u_{t-N+1}, \cdots, v_t]$로 사용하는 것이다. 이때 Item Embedding과 Position Embedding의 Dimension의 크기는 동일하게 $d$로 가지고 가야된다.
Output Layer
Output Layer는 간단하다. 최종 L 번째 Layer의 출력값인 $h^L_t$와 Item Embedding $E \in \mathbb{R}^{|\mathcal{V}| \times d} $를 곱하여 각 제품별 확률값을 도출하고, 이를 바탕으로 다음 클릭 혹은 구매할 제품을 예측한다.
\[ P(v) = \text{softmax}(\text{GELU} ( h^L_t W^P + b^P ) E^{\top} + b^O ) \]
Model Learning
Model Learning 단계에서는 [MASK] 된 단어를 맞추는 태스크를 진행한다. t+1 시점에 올 제품을 예측하는 Test 단계에서는 [MASK] Token을 마지막에 두어 이를 예측하는 형태로 진행한다.
\[ \text{Input}: [v_1, v_2, v_3, v_4, v_5] \overset{\text{randomly mask}}{\longrightarrow} [v_1, [\text{mask}]_1, v_3, [\text{mask}]_2, v_5] \]
\[ \text{Labels}: [\text{mask}]_1 = v_2, \quad [\text{mask}]_2 = v_4 \]
이때의 손실 함수는 아래와 같이 사용한다.
\[ \mathcal{L} = \frac{1}{|\mathcal{S}^m_u|} \sum_{u_m \in \mathcal{S}^m_u} -\log P(v_m \ v^*_m | \mathcal{S}^{\prime}_u ) \]
$\mathcal{S}^{\prime}_u$는 Masking된 Sequence $\mathcal{S}_u$를 의미한다. $\mathcal{S}^m_u$는 Masking된 제품을 의미하고, $v^*_m$는 마스킹 된 제품의 정답 라벨을 의미한다.
Experiments
본 연구에서는 Beauty, Steam, MovieLens 데이터를 사용하여 실험하였으며, POP(Best Seller), BPR-MF, NCF, FPMC, GRU4Rec, GRU4Rec+, Caser, SASRec을 Baseline 모델로 사용하였다. 실험 결과는 당연하게 BERT4Rec의 성능이 가장 우수한 것을 확인할 수 있다.

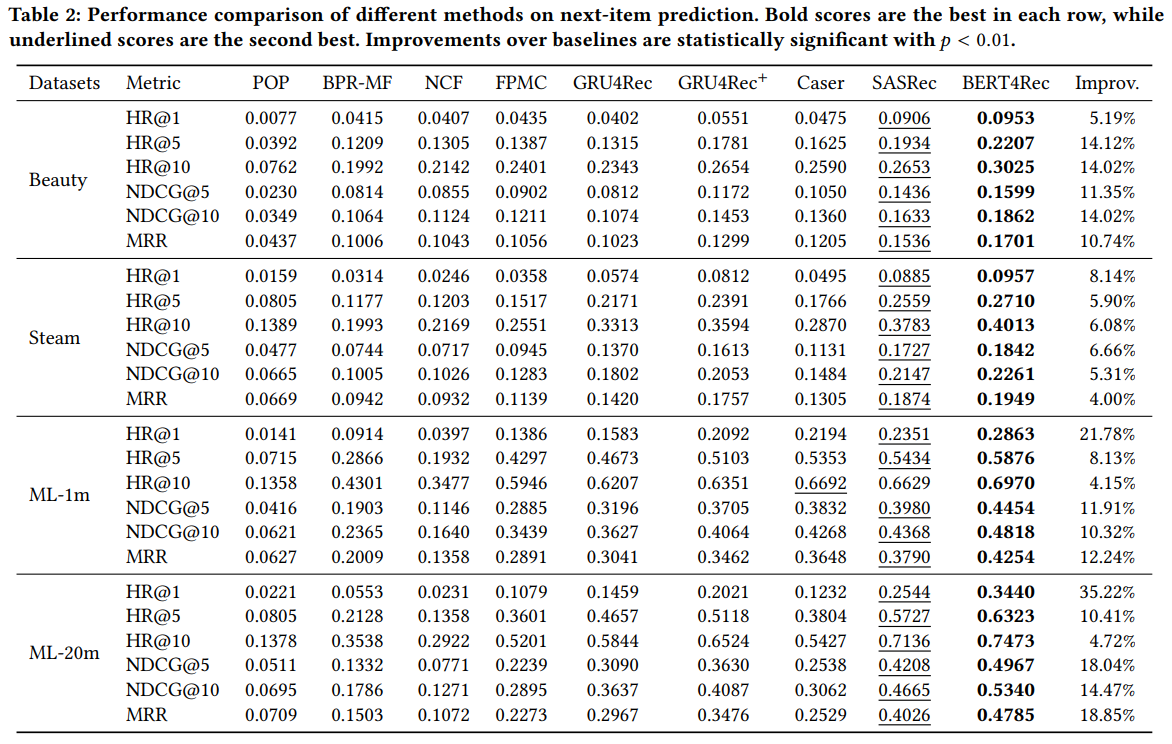
RQ1) Do the gains come from the bidirectional self-attention model or from the Cloze objective?
SASRec의 경우 BERT4Rec 구조에서 Bidirectional이 아니라 left-to-right 모델이다. 실험 결과를 통해 Bidirectional 구조가 left-to-right 모델보다 우수한 것을 확인하였고, Masking을 하나만 했을 때와 $\rho$로 지정해 더 많은 Masking을 했을 때 성능이 우수한 것을 확인할 수 있다.

RQ2) Why and how does bidirectional model outperform uni-directional model?
RQ1을 통해 Bidirectional 기법이 성능이 우수한 것을 확인하였다. 그렇다면 왜 Bidirectional 기법의 성능이 우수한 것일까? 아래의 그림에서 Layer1을 살펴보면 Head1의 경우 왼쪽 부분에 Attention을 하는 경향이 있고, Head2의 경우에는 오른쪽에 있은 Item에 Attention을 하는 경향이 있다. 또한, Layer2의 경우에는 근처의 Item에 Attention하는 경향을 보인다. BERT2Rec의 경우 Layer=2로 지정하였기 때문에 Layer2는 출력 층과 연결되어 있기 때문에 최근 항목의 다음 항목을 예측하는 데 더 중요한 역할을 하기 때문이다. Bidirectional 기법을 사용하지 않는다면, Layer1에서의 결과를 파악할 수 없기 때문에 Bidirectional 기법의 성능이 우수한 것으로 확인된다.

Impact of Hidden Dimensionality, Mask Proportion and Sequence Length
$d$의 경우 64인 경우에 가장 우수한 성능을 보이는 경우도 있고, MovieLes의 경우에는 차원의 크기가 커지면 커질수록 성능이 증가하는 추세를 보이고 있다. Mask Proportion $\pho$의 경우에는 데이터의 구성에 따라 0.2, 0.4, 0.6 등 다양한 결과가 도출된다. Sequence Length $N$의 경우에도 마찬가지로 데이터 셋의 구성에 따라 최적의 길이가 달라진다.



Ablation Study
Ablation Study에서는 Position Embedding (PE), Position-wise Feed Forward Network (PFFN), Layer Normalization (LN), Residual Connection (RC), Dropout, Layer Number $L$, Head Number $h$의 영향을 확인하기 위한 실험을 진행하였다.
