Contents
기존 연구에서 주로 사용하는 Sequential Recommendation은 Local Context Information을 사용하거나 오직 Item Loss만을 사용해서 구축하고 있기 때문에, Sequence Representation을 제대로 학습하지 못한다는 문제점을 언급하며, 이를 해결하기 위해 Weighted Item Transition Graph (WITG)를 사용하는 Graph Contrastive Learning for Sequential Recommendation (GCL4SR) 기법을 제안하는 논문이다.
Introduction
Sequential Recommendation의 State-of-the-art (SoTA) 모델들은 우수한 성능을 보이고 있으나, 다음과 같은 문제점이 존재한다. 첫 번째, 기존 기법들은 User Interaction을 개별적으로 모델링하고 Local Context만을 사용한다. 이와 같은 방법은item 내의 subsequence를 고려하지 못한다. 두 번째, User Behavior은 매우 Sparse하다. 기존 연구의 경우 오로지 Item 정보만을 수행하기 때문에 데이터가 매우 Sparse해서 추천 성능이 제대로 발현되지 않는다. 세 번째, Sequential Recommendation은 주로 Implicit Feedback Sequence를 입력으로 사용하는데, 이와 같은 데이터는 노이즈(Noise)가 존재할 수 있다.
본 연구에서는 위 세가지의 문제를 해결하고자 먼저, Item Transition Pattern을 파악하기 위해 Weight Item Transition Graph (WITG) 기법을 구축한다. WITG는 Global Context Information을 제공할 수 있다. 그 다음으로, Data Sparse 문제를 해결하기 위해 WITG 에서 이웃을 샘플링(Sampling)해 각 Interaction Sequence View를 증강(Augmentation)한다. 그런 다음, 그래프 대조학습(Contrastive Learning) 기법을 적용해 증강된 View를 바탕으로 학습한다. 이와 같은 기법은 Global Context Information을 통합(Incorporate)할 수 있는 것뿐만 아니라, 각 Item Transition의 중요도를 설명하고 노이즈의 영향을 약화시킬 수 있다. 본 연구에서는 위 과정을 적용한 Graph Contrastive Learning for Sequential Recommendation (GCL4SR) 기법을 제안하였다.
Preliminaries
사용자는 $u \in U$, 제품은 $v \in V$, Interaction Sequence의 집합은 $D$, Interaction Sequence는 $S = \{v_1, v_2, \cdots, v_n\}$로 표기한다. $n$는 Interaction안에 존재하는 제품의 총 길이를 의미한다. 사용자 $u$에 대한 Embedding Vector는 $p_u \in \mathbb{R}^{1 \times d}$로 표기하고, 제품 $i$의 Embedding Vector는 $e_i \in \mathbb{R}^{1 \times d}$, t 시점의 $S$의 initial Embedding은 $E^{(0)}_S \in \mathbb{R}^{n \times d} $로 표기한다. 모든 제품에 대한 Embedding은 $E \in \mathbb{R}^{|V| \times d}$로 표현할 수 있다.
기존 연구와 다른 점은 모든 Users; Behavior Sequence에 대한 Item Transition Patterns의 Global View를 제공하기 위해 $D$에서 WITG $\mathcal{G}$를 구축해야 된다는 것이다. $v_t \in S$가 있다고 할 때, $v_t$와 $v_{(t+k)}$간의 edge가 있으면, edge weight를 $w(v_t, v_{(t+k)})$ $\leftarrow$ $w(v_t, v_{(t+k)}) + 1/k$로 업데이트한다. 만약 edge가 존재하지 않는다면, edge weight $w(v_t, v_{(t+k)}) $를 $1/k$로 설정한다 $(k \in \{1, 2, 3\})$. 이때, $1/k$는 Sequence에서 k-hop neighbor $v_{(t+k)}$에 대한 target node $v_t$의 중요도를 의미한다. 모든 $D$에 대해 위 과정을 반복한 후, 아래와 같이 re-normalize를 수행한다.
\[ \hat{w}(v_t, v_j) = w(v_t, v_j)\cdot ( \frac{1}{\text{deg}(v_t)} + \frac{1}{\text{deg}(v_j)}) \]

The Proposed Recommendation Model
본 연구에서 제안하는 GCL4SR는 총 4단계로 구성되어 있다. 1) Graph Augmented Sequence Representation Learning, 2) User-specific Gating, 3) Basic Sequence Encoder, 4) Prediction Layer.

Graph Augmented Sequence Representation Learning
WITG $\mathcal{G}$가 입력으로 들어오면, 먼저 $v$를 Central Node로 취급하고, 샘플링 Depth M=2, 샘플링 크기 N=20으로 설정하여 Interactive하게 $\mathcal{G}^{\prime}_S = ( V^{\prime}_S, E^{\prime}_S, A^{\prime}_S)$와 $\mathcal{G}^{\prime \prime} = (V^{\prime \prime}_S, E^{\prime \prime}_S, A^{\prime \prime}_S)$를 생성한다.
그런 다음, Graph Neural Network를 사용하여 $G^{\prime}$과 $G^{\prime \prime}$을 인코딩한다. $\mathcal{G}^{\prime}_S$를 예로 들면 아래와 같은 수식으로 표현할 수 있다.
\[ a^{(t)}_{v_i} = \text{Aggreate}^{(t)} (\{ h^{(t-1)}_{v_j} : v_j \in N^{\prime}_{v_i} \} )\]
\[ h^{(t)}_{v_i} = \text{Combine}^{(t)} (a^{(t)}_{v_i}, h^{(t-1)}_{v_i} ) \]
본 연구에서는 첫 번째 Layer는 GCN 기법을 따라 사용하였으며, 이후에는 GraphSage 방법을 따라 Layer를 쌓아서 사용하였다. 그 다음으로는 Graph Contrastive Learning Objective, 즉, Contrastive Loss를 측정하는 단계다.
\[ \mathcal{L}_{GCL} (S) = \sum_{S \in D} - \log \frac{\exp( cos(z^{\prime}_S, z^{\prime \prime} ) / \tau ) }{\sum_{K \in D} \exp ( cos ( z^{\prime}_S, z^{\prime \prime}_K ) / \tau ) } \]
User-specific Gating
개별 사용자들은 제품의 일부 특정 속성에만 관심이 있을 수 있기 때문에 Global Context Information은 User-specific 해야 된다. 본 연구에서는 기존 연구를 참고하여 개인 취향에 맞는 Global Context Information을 캡쳐하기 위해 User-specific Gating Mechanism을 사용하였다.
\[ Q^{\prime}_S = H^{\prime}_S \otimes \sigma (H^{\prime}_S W_{g1} + W_{g2} p^{\top}_u) \]
$W_{g1} \in \mathbb{R}^{d \times 1}$과 $W_{g2} \in \mathbb{R}^{n \times d}$는 가중치 행렬을 의미하고, $\otimes$는 원소별 곱(Element-wise Product)을 의미한다. $Q^{\prime \prime}$도 위와 동일한 방식으로 얻을 수 있다.
그다음 단계는 Representation Alignment Objective 단계다. 해당 단계에서는 Maximum Mean Discrepancy (MMD)를 사용하여 학습한다. 즉, $Q^{\prime}_S$와 $Q^{\prime \prime}_S$ 분포 간의 거리를 측정한다는 것을 의미한다. 이때 Loss를 도출해 거리를 최소화하는 방향으로 학습한다. 일단 MMD 는 아래와 같은 수식으로 계산된다 ($X \in \mathbb{R}^{m \times d}$, $Y \in \mathbb{R}^{\tilde{m} \times d}$).
\[ \begin{equation} \begin{split} MMD(X, Y) & = \frac{1}{m^2} \sum^m_{a = 1} \sum^{m}_{b=1} \mathcal{K}(x_a, x_b) \\ \\ & + \frac{1}{\tilde{m}^2} \sum^{\tilde{m}}_{a=1} \sum^{\tilde{m}}_{b=1} \mathcal{K}(y_a, y_b) - \frac{2}{m \tilde{m}} \sum^m_{a=1} \sum^{\tilde{m}}_{b=1} \mathcal{K}(x_a, y_b) \end{split} \end{equation} \]
$\mathcal{K}(\cdot, \cdot)$는 Kernel Function을 의미하고, $x_a, y_b$는 각각 $X$의 a 번째 행, $Y$의 b 번째 행을 의미한다. 본 연구에서는 Gaussian Kernel을 사용하고 Bandwidth $\rho$를 지정해 사용하였다. ($e^{-\frac{||x-x^{\prime} ||^2}{2 \rho ^2}})$
\[ \mathcal{L}_{MM}(S) = MMD(E^{(0)}_S, Q^{\prime}_S ) + MMD (E^{(0)}_S, Q^{\prime \prime}_S ) \]
Basic Sequence Encoder
세 번째 단계는 Basic Sequence Encoder 단계다. 해당 기법은 SASRec을 골조로 해서 아래와 같은 수식으로 인코딩한다.
\[ H^l = FFN (Concat (head_1, \cdots, head_h ) W^h ) \]
\[ head_i = Attention(H^{l-1} W^Q_i, H^{l -1} W^k_i, H^{l-1} W^V_i ) \]
\[ Attention(Q, K, V) = softmax(\frac{QK^{\top}}{\sqrt{d}} ) V \]
$FFN(\cdot)$는 Feed-Forward Network를 의미하고, $h$는 head의 수를 의미한다. $W^Q_i$, $W^K_i$, $W^V_i \in \mathbb{R}^{d \times d/h}$, $W^h \in \mathbb{R}^{h \times h}$ 는 가중치 행렬을 의미한다. Attention Network는 scaled dot product를 사용하였다.
Prediction Layer
Prediction Layer는 단순히 도출된 결과를 곱하는 것이 끝이며, 아래와 같은 수식으로 표현가능하다.
\[ M = Attention(Concat(Q^{\prime}_S, Q^{\prime \prime}_S, H^l ) W_T ) \]
\[ \hat{y}^{(S)} = softmax(ME^{\top} ) \]
Multi Task Learning
Sequential Recommendation은 다음 제품을 예측하는 것에 초점을 두고 있다. 본 연구에서는 목적에 맞게 Seuqence $S_u = \{ v^1_u, v^2_u, \cdots , v^{|S_u|}_u\}$를 SubSequence로 분할하여 학습하였다. 즉, $\{ (S^{1:1}_u, v^2_u), (S^{1:2}_u, v^3_u), \cdots, (S^{1: |S_u| -1}_u, v^{|S_u|}_u) \}$로 사용하여, 학습하였다. 이와 같이 데이터를 새롭게 구성하는 이유는 단순히 Sequence가 들어왔을 때보다 훨씬 많은 데이터를 학습할 수 있기 때문이다.
\[ \mathcal{L}_{main} = - \sum_{S_u \in D} \sum^{|S_u| -1}_{k=1} \log ( \hat{y}^{(S^{1:k}_u)} (v^{k+1}_u ) ) \]
위 과정을 전체적으로 종합하면 본 연구에서는 $\mathcal{L}_{main}$, $\mathcal{L}_{GCL}$, $\mathcal{L}_{MM}$ Loss를 사용하게 된다. 따라서, 본 연구의 최종 Loss Function은 아래와 같이 정의할 수 있다.
\[ \mathcal{L} = \mathcal{L}_{main} + \sum_{S_u \in D} \sum^{|S_u| -1}_{k=1} \lambda_1 \mathcal{L}_{GCL} (S^{1:k}_u) + \lambda_2 \mathcal{L}_{MM} (S^{1:k}_u ) \]
$\lambda_1$, $\lambda_2$는 Hyper-paramter가 된다.
Experiments
본 연구에서 제안하는 GCL4SR의 성능을 검증하기 위해 LightGCN, FPMC, GRU4Rec, Caser, SASRec, HGN, SR-GNN, GC-SAN, GCE-GNN, S$^3$-Rec, CL4SRec 등의 state-of-the-art 기법을 베이스라인 모델로 사용하여 실험을 진행하였다. 실험의 세부 카테고리는 Performance Comparison, Ablation Study, Sensitivity Study, Impact of Sequence Encoder으로 구분지을 수 있다.
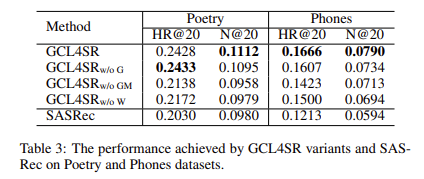
Performance Comparison은 기존의 SoTA 모델과 성능을 비교했을 때 어떤 성과를 보이는지 (Table 2)를 다루고 있고, Ablation Study는 본 연구에서 제안하는 GCL4SR 기법의 구성요소 즉, Graph Contrastive Loss, MMD, edge Weight 등의 요소를 제거했을 때 성능 차이가 있는지를 기술한다. Sensitivity Study는 본 연구의 Hyper-parameter를 달리 설정했을 때 성능의 변화가 있는지를 실험한 것이며, 마지막 Impact of Sequence Encoder는 다양한 Sequence Encoder를 사용했을 때 성능 차이가 존재하는지 확인하는 실험이다. 본 연구에서는 SASRec, GRU, HGN을 사용하여 성능을 비교하였으며, SASRec의 성능이 가장 우수한 것을 확인하고 이를 채택하여 사용하였다.