Contents
Point-of-interest (POI)는 장소를 추천하는 Task라고 볼 수 있다. 기존 POI 연구에서는 대부분 User와 Location을 따로 분리하여 모델링하고 있으며, 사용자의 장소에 대한 시공간적 수용(Acceptance) 범위를 무시하고 있다. 본 연구에서는 이와 같은 문제를 해결하고자, Knowledge Graph with Temporal information (TKG)를 구성하여 Timestamp와 User, Location을 함께 고려하고자 TKG를 기반으로 한 Spatial-Temporal Graph Convolutional Attention Network (STGCAN) 기법을 제안한다.
Introduction
POI Recommendation은 사용자가 선호할 만한 장소를 추천하는 것에 초점을 두고 있다. 이는, Location-based Social Networks (LBSNs)에서 중요한 역할을 수행하고 있다. 본 연구에서는 real life에서 다음과 같은 것들을 확인하였다. 1) Personal Preference: 같은 장소라도, 개인의 선호에 따라 다른 장소로 간주할 수 있다. Figure 1을 살펴보면 User A는 카페를 Dining Place로 이용하고 있으나, User B는 12:00시에 Social Place로 이용하였다. 2) Dynamic preference: 같은 장소라도 시간에 따라 다른 장소로 간주될 수 있다. User B는 12:00시에는 카페를 Social Place로 사용하였으나, 17:00시에는 Dining Place로 사용하였다. 3) Personal acceptance to distance/time: Figure 3을 보면 Location $L$은 User B가 User A에 비해 방문할 확률이 높다. User B와 User A의 이동 궤도(Trajectory)를 살펴보면 User B는 보다 먼 지역도 자주 다녀온 것을 확인할 수있고, User A 는 비교적 본인의 위치에서 가까운 장소를 많이 방문하는 궤도를 보이고 있기 때문이다.


기존 연구는 대부분 User와 Location을 따로 분리하여 Sequence를 학습하였기 때문에 Dynamic Preference를 제대로 학습하지 못한다. 또한, 위치에 대한 시간적, 거리적 수용범위를 고려하지 않고 있다. 따라서, 본 연구에서는 위와 같은 문제를 해결하기 위해 Temporal Information을 고려한 Knowledge Graph (TKG)를 사용한 Spatial-Temporal Graph Convolutional Attention Network (STGCAN) 기법을 제안하였다.
Problem Description
$Y$는 GPS 정보와 TKG $\mathcal{G}$ 기반 사용자가 방문한 Sequence를 의미한다. 입력으로 $Y$가 들어오면 위치에 대한 확률 행렬 $P$를 출력한다. 각 Sequence $Y$는 $(u_i, l_i, t_i)$로 구성되어 있으며, $u_i$는 사용자 $l_i$는 장소 $t_i$는 방문한 시간을 의미한다. TKG $\mathcal{G}$ = $\{ (e_u, r, e_l, t)|$$e_u \in E_u$, $e \in R$, $e_l \in E_l$, $t \in T \}$에서 $e_u$, $e_l$는 User Entity, Location Entity를 의미하고, $r$는 Relation을 의미한다. $\mathcal{G}$는 다시 Timestamp를 기준으로 분할할 수 있으며, 분할하면 $\mathcal{G} = \{G_1, G_2, \cdots, G_t\}$가 된다.
본 연구에서는 시간적 공간적 수용 범위를 고려하기 이해 Receptive Field를 도입하는데 사용자와 장소에 대한 Receptive Field는 $H^{(D)}_{U / L, U}$로 표기한다. $D$는 Depth를 의미하고, $e_{u^{\prime} / l^{\prime} }$는 사용자/장소의 Neighbour Entity를 의미하고, $N^{u/l}$는 Neighbour Entity 집합을 의미한다. Neighbour Entity는 Target Entity와 관련있는 Entity를 의미한다.
Methodology
STGCAN 기법은 총 4 단계로 구성되어 있다. 1) Embedding Layer, 2) User Neighbour Aggregation Layer, 3) Location Neighbour Aggregation Layer, 4) Spatial-Temporal Interval Aware Attention Layer.
Embedding Layer
History Visit Sequence $Y$는 24 $\times$ 7 로 구성되어 있다. 즉, 총 7일간 24시간 동안의 Sequence 정보를 담고 있다. 그런 다음, $U$, $L$, $T$를 Embedding 하여 $E_U \in \mathbb{R}^{N \times E}$, $E_L \in \mathbb{R}^{M \times E}$, $E_T \in \mathbb{R}^{K \times E}$를 생성한다. $E$는 임베딩 사이즈를 의미한다.
Neighbour Aggregation Layer
이번 단계는 Neighbour 정보를 Aggregation해서 Embedding을 업데이트하는 단계다. 본 연구에서는 TKG 를 사용하기 때문에 Triple이 아닌 Quadruple $(e_u, r, e_l, t)$ in $\mathcal{G}$로 구성된다. 이때 $e_u$의 Neighbour Entitiy는 $t$시점 이전에 같은 Location을 방문한 $e_{u^{\prime}}$으로 정의한다. $(e_{u^{\prime}}, r, e_l, t^{\prime} ) ( t^{\prime} < t) $. 본 연구에서는 $K$ 개의 이웃을 선택하여 이를 구축한다. 그렇다면 Neighbour Entity는 $N^u_t = \{ e^{u^{\prime}, 1}_t, e^{u^{\prime}, 2}_t, \cdots, e^{u^{\prime}, K}_t \} $가 된다. (Figure 4 참고)
그런 다음, Target User에 대한 K Neighbour Entities의 관련성을 구별하기 위해 Relation $r$은 Spatial-tenporal Scoring Function $I$를 이용하여 재정의할 수 있다.
\[ \lambda^{u, u^{\prime}}_{st} = I = I_s + I_t + I_t \{ (e_u, r, e_l, t), (e_{u^{\prime}}, r, e_l, t^{\prime} )\} = \exp ( - \gamma | t - t^{\prime} | ) \]
$\gamma$는 hyper-parameter를 의미한다. 위 수식을 통해 $N^u_t$내 존재하는 Neighbour Entity에 대한 각각의 $\lambda^{u, u^{\prime}}_{st}$를 구할 수 있다. 그런 다음, 각 Score를 바탕으로 Softmax를 수행해 각 Layer에 따른 가중치를 계산하고 Linear Function을 사용하여 $e^u_t$를 업데이트한다.
\[ \alpha^{u, i}_{st} = \frac{ \exp (\lambda^{u, i}_{st}) }{ \sum^K_{i = 1} \exp ( \lambda^{u, i}_{st} ) } \]
\[ e^u_t \leftarrow e^u_t + \sigma ( \sum^K_{i=1} \alpha^{u, i}_{st} \cdot e^{u^{\prime}, i}_t ) \]
위 과정을 통해 각 Depth $D$에 대해서 수행하는 것을 수식으로 표현하면 아래와 같이 표현할 수 있다.
\[ e^u_t [h + 1] = e^u_t + \sigma ( \sum^K_{i=1} \alpha ^{u, i}_{st} \cdot e^{u^{\prime}, i}_t [h] ) \]

Location Neighbour Aggregation Layer
위에서는 User-Receptive-Field를 생성하여 User Neighbour Aggregation을 수행하였다면, 이번 단계는 Location에 대한 Neighbour Aggregation을 수행하는 단계다. User Neighbour 을 구하는 단계에서는 Location Entity는 고정인 상태에서 시점이 바뀔 때 User Neighbour Entity를 Aggregation 했다면, Location Neighbour에서는 User와 Location 둘다 변화한다. 구체적으로, Location의 이웃을 구할 때에는 사용자와 그 사용자의 과거 기록에 의해 결정되기 때문에, 특정 사용자로부터 다양한 Location 이웃을 가지게 된다.
이를 수식으로 표현하면 $(e_u, r, e_l, t)$의 이웃은 $(e_{u^{\prime}}, r, e_{l^{\prime}}, t^{\prime}) (t^{\prime} < t)$가 된다. 본 연구에서는 Neighbour Entitiy를 연결(Concatenate)하여 $N^u = Concat(N^u_t | t \in T)$로 표현하고, Lower Bound Function을 활용하여 $t$보다 크지 않은 $\hat{t}$ 시점을 가진 Location Entity를 선택한다. 복잡하게 작성되어 있으나, t 이전 시점의 값들을 가지고 온다는 것이다.
위 과정을 수행하면, 특정 사용자 $u$에 대한 $K$ Location Neighbour Entities는 $N^{l, u}_t = \{ e^{l^{\prime}_1, u}_t, e^{l^{\prime}_2, u}_t, \cdots, e^{l^{\prime}_K, u}_t \} $가 된다. (Figure 5 참조). 그런다음 $K$ Location Neighbour의 관련성을 구별하기 위해 아래와 같은 수식을 통해 $I_s, I_t$에 대한 관련성을 구한다.
\[ \lambda^{l, l^{\prime}_u}_{st} = I = I_s + I_t \]
\[ I_s = I_s(GPS_l, GPS_{l^{\prime}_u}) = \frac{1}{\theta + H(GPS_l, GPS_{l^{\prime}_u} ) } \]
\[ I_t = I_t \{ (e_u, r, e_l, t ), (e_{u^{\prime}}, r, e_{l^{\prime}}, t^{\prime} ) \} = \frac{1}{ \theta + |t - t^{\prime} | } \]
이와 같은 수식을 사용하는 이유는 두 Location 간의 하버사인 거리(Haversine Distance)를 구하기 위함이다. 위 수식을 계산한 후 아래의 수식을 통해 최종 임베딩 벡터를 생성한다.
\[ \alpha^{l, l^{\prime}_u}_{st} = \frac{ \exp(\lambda ^{l, l^{\prime}_u})}{\sum^K_{i=1} \exp ( \lambda ^{l, l^{\prime}_u}_st )} \]
\[ e^{l, u}_t \leftarrow e^{l, u}_t + \sigma ( \sum^K_{i=1} \alpha^{l, l^{\prime}_u}_{st} \cdot e^{l^{\prime}_u} ) \]
\[ e^{l, u}_t [h+1] = e^{l, u}_t + \sigma ( \sum^K_{i=1} \alpha^{l, l^{\prime}_u}_{st} \cdot e^{l^{\prime}_u}[h]) \]

Spatial-Temporal Interval Aware Attention Layer
이번 단계는 Neighbour Aggregation 후, 공간적 거리와 시간 간격을 측정하고, 가중치를 Representation에 할당해 최종 Representation을 도출하는 단계다. Spatial Distance를 $\Delta s$라고 하고, Time Interval을 $\Delta t$라고 하면, 각 Sequence에서 $\Delta s$, $\Delta t$를 바탕으로 아래의 수식과 같이 Spatial-temporal interval을 계산한다.
\[ d_s = \frac{ [ vsl \cdot (\Delta s_{max} - \Delta s ) + vsu \cdot ( \Delta s - \Delta s_{min} ) ] \cdot inv_s }{(\Delta s_{max} - \Delta s_{min}) + \theta } \]
\[ d_t = \frac{ [vtl \cdot ( \Delta t_{max} - \Delta t ) + vtu \cdot ( \Delta t - \Delta t_{min} ) ] \cdot inv_t }{(\Delta t_{max} - \Delta t_{min} ) + \theta } \]
이때 $\Delta *_{max \ or \ min}$는 Spatial, Time에 대한 upper bound, lower bound를 의미한다. $vsl$, $vsu$, $vtl$, $vtu \in \mathbb{R}^E$와 $inv_s$, $inv_t \in \mathbb{R}^{N \times E}$는 Trainable Parameter를 의미한다. 그 후 Self-Attention을 통해 $U$와 $L$을 계산하고, 이를 곱하여 최종 $P$ 행렬을 도출한다.
\[ U_{Att} = W_d \cdot (E_U + E_L + E_T ) + b \]
\[ L_{Att} = W^Q [ W_d \cdot ( E_L + E_T)]^{\top} + b \]
\[ P = (L_{Att})^{\top} \times U_{Att} \]
Neural Network Training
본 연구에서는 Cross-Entropy Loss 를 사용하였으며, 최종 Loss Function은 아래와 같이 정의된다.
\[ \mathcal{L} = - \sum_{j \in L}( \log \sigma (p_j) + \sum^s_{j^{\prime} \in L} \log \sigma (1 - p^N_{j^{\prime}})) - \lambda \Theta \]
이때 $\Theta$는 $vsu, usl, vtu$등과 같은 모든 Parameter를 의미한다. 즉, 파라미터에 대한 규제항을 의미한다.

Experiments
본 연구에서는 NYC, TKY, Gowalla와 같은 POI Recommendation Task에서 주로 사용하는 데이터를 통해 실험을 진행하였으며, BPR-MF, PRME, TransRec, DeepMove, KGCN, TiSASRec, GeoSAN, STAN, CyGNet 등과 같은 POI Recommendation을 위한 SoTA 모델을 베이스라인으로 사용하였다. 실험에서 특이한 점은 $Imp@K$라는 Metric을 새로 정의하여 사용하였으며, 이는 STGCAN 의 Recall에서 베이스 라인의 Recall 값을 뺀 후 정규화한 값을 의미하고 아래의 수식과 같이 계산된다.
\[ Imp@K = \frac{ \dot{R}_{STGCAN}@K - R@K}{R@K} - \sum_{i < K} Imp@i \]
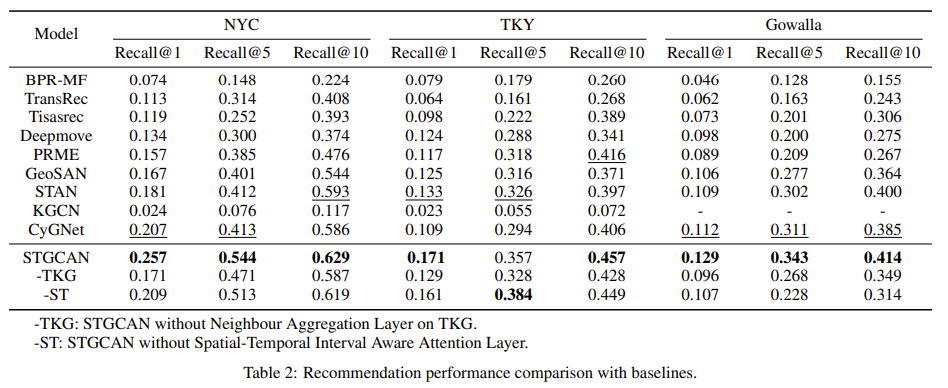
실험은 총 4가지로 구성하였다. 1) Comparison Performance 2) Impact of Embedding Dimension 3) Impace of Depth of receptive field 4) Impact of neighbour entity size. Comparison Performance는 Table 2, Figure 6과 같이 베이스라인 모델과 비교했을 때의 STGCAN 기법의 성능에 대한 결과를 나타낸다. Impact of * 는 각각에 대한 영향이 어느정도인지 확인하는 실험이다. Figure 7, Table 3, Table 4를 통해 확인할 수 있다.