Contents
GSL4Rec 기법은 빠르게 변화하는 소셜 네트워크에 적용하기 위해 확장성(Scalability)과 유효성(Effectiveness)이 고려된 기법이다. GSL4Rec 기법은 Coarse Neighbor Screening과 Self-adaptive Graph Sructure Learning 총 2 stage로 구성되어 있다. 또한, 단계별 휴리스틱 방법을 적용하여 더 쉽게 Global Optima에 도달하도록 만들어 효율성을 향상시켰다.
Introduction
Session-based Recommendation은 Session 안의 사용자의 행동을 기반으로 사용자가 선호하는 것을 예측하는 것을 목표로 한다. 최근에는 사용자 간의 관계 등과 같은 정보를 추가로 고려하는 Session-based Social Recommendation 관련 연구가 많이 진행되고 있으며, 가장 성공적인 기법 중 하나는 바로 Graph Neural Network를 적용한 Session-based Recommendation이다. 그러나 위 기법은 미리 정의된 Social Network를 가정하고 Static Graph를 이용하여 사용자 간의 패턴을 학습하고 있으나 여전히 다음과 같은 두 가지 한계점이 존재한다. 1) Social Network를 그래프로 표현하는 것은 매우 Expensive하며, 사전에 그래프가 구축되지 않으면 기존 방법을 적용하는 것이 불가능하다. 2) Social Relationship은 주로 정적(Static)이고 사용자 간의 공유된 선호도가 반드시 일관되지는 않는다. 구체적으로, 유사한 선도를 공유하는 두 사용자는 서로를 모를 수도 있다. 즉, Social Network에서는 단순히 유사한 선호도만을 고려하는 것이 아니라 사용자와 사용자 간의 관계까지도 고려해야된다는 것이다.
본 연구에서는 1) 확장성 (Scalability)과 2) 효율성 (Effectiveness)을 다루기 위해 Graph Structure Learning framework for Session-based Recommendations (GSL4Rec) 기법을 제안하였다 (Figure 1). 먼저 확장성 문제를 다루기 위해 Two-Stage 전략을 사용한다. 첫 번째 Stage는 Coarse Neighbor Screening 이며, 이는 Lightweight Function을 사용해 모든 사용자에 대한 $k_1$개의 이웃을 가져온다(Candidate Neighbor Pool). 두 번째 Stage는 Self-adaptive Graph Structure Learning이며, 이는 이전 Stage의 결과를 바탕으로 $k_2$개의 이웃을 선정한다. 이때 $k_2 < k_1 \ll n$이 되어야 한다. 그 다음으로는 효율성을 다루기 위해 휴리스틱 학습 전략을 제안한다. 이 방식은 기존 소셜 네트워크의 Value를 극대화하여 Warm Up된 시작지점에서 시작할 수 있도록 만들고, 학습을 효율적으로 할 수 있다.

Problem Definition
Session-based Recommendation의 Definition은 다음과 같다. 사용자 집합은 $\mathcal{U}$라 하고, 제품 집합은 $\mathcal{I}$라 한다. $u \in \mathcal{U}$의 time Step $\mathcal{T}$의 Behavior은 $H^u_T = \{ S^u_1, S^u_2, \cdots, S^u_T \}$로 정의하고, 이때 $S^u_t$는 $t$ 시점의 $u$의 Session을 의미한다. $S^u_t = \{ i^u_{t, 1}, i^u_{t, 2}, \cdots, i^u_{t, n^u_t} \}$가 되고, $n^u_t$는 $u$의 $t$ 시점에 존재하는 전체 제품의 수를 의미한다. $S^u_{T+1}$ = $\{ i^u_{T+1, 1}$, $i^u_{T +1, 2}$, $\cdots$, $i^u_{T+1, m} \}$이 주어지면, Session-based Recommendation은 Next Step인 $i^u_{T+1, m+1}$이 무엇인지 예측하는 것이 목적이다.
Session-based Social Recommendation의 Definition은 다음과 같다. $\mathcal{G} = <\mathcal{U}, \mathcal{E} > $를 Social Network로 정의하고, $\mathcal{U}$는 사용자 집합 $\mathcal{E}$는 Link 집합으로 정의한다. 새로운 Session $S^u_{T+1}$ $\{ i^u_{T+1, 1}$, $i^u_{T+1, 2}$, $\cdots$, $i^u_{T+1, m} \}$이 주어지면, $i^u_{T+1, m+1}$를 예측한다. 이때, Session-based Recommendation과는 달리 이웃 노드의 정보를 취합하여 $S^k_T$를 생성한다.
Graph Structure Learning for Recommendation의 Definition은 다음과 같다. $\mathcal{G}_0 = < \mathcal{U}, \mathcal{E}_0 > $라고 정의하면, Session-based Social Recommendation과 같이 추천하는 것 외에도, 추천 성능을 향상시키기 위해 사용자 간의 Dynamic Link 까지도 예측한다. $\{ \mathcal{E}_1, \mathcal{E}_2, \cdots, \mathcal{E}_{T+1} \} $
Methodology
본 연구에서 제안하는 GSL4Rec은 1) Coarse Neighbor Screening Layer, 2) Dynamic Interest Modeling, 3) Self-adaptive Graph Structure Learning, 4) Attentive Interest Propagation Layer로 구성되어 있다.

Coarse Neighbor Screening Layer
먼저, Target Node와 Source Node에 대한 Embedding을 $E_{tar}, E_{src} \in \mathbb{R}^{N \times d}$으로 정의하고, 아래의 수식을 통해 확률 값이 높은 Top@K개의 $S$를 선정한다.
\[ S = \text{ReLU}(\text{tanh}(E_{tar} E^{\top}_{src})) \]
Dynamic Interest Modeling
Dynamic Interest Modeling은 Short-term Interest와 Long-term Interest로 구성된다. Short-term Interest에서는 LSTM 기법을 활용하여 학습한다. 모델의 입력으로 $S^u_T = \{ i^u_{T, 1}, i^u_{T, 2}, \cdots, i^u_{T, m} \}$이 주어졌을 때, 아래와 같은 수식으로 $s^u_T$를 도출할 수 있다.
\[ s^u_T = s^u_{T, m} = \text{LSTM}(i^u_{T, m}, s^u_{T, m-1} ) \]
Long-term Interest에서는 $E_{src}$를 재사용하여 Long-term Interest를 학습한다.
\[ l^u = E_{src} [u, :] \]
$E_{src} [ u, :]$는 $E_{src}$의 u번째 Row를 의미한다. 그런 다음 Short-term Interest와 Long-term Interest를 연결(Concatenate)하여 최종 값을 도출한다.
\[ p^k_{src} = \text{ReLU} (W_1 concat ([ s^k_T, l^k ] )), \quad k \in N_u \]
$W_1 \in \mathbb{R}^{d \times 2d}$는 학습가능한 가중치 행렬을 의미한다. 본 연구에서는 $u$의 Next Step Session을 예측하는 것에 초점을 두기 때문에, Short-term Interest를 바탕으로 $p^u_{tar}$를 예측한다.
\[ p^u_{tar} = s^u_{T+1} \]
Self-adaptive Graph Structure Learning
이번 단계는 이전 단계에서 전달 받은 Short-term Interest 정보를 바탕으로 Two-layer Neural Network를 사용해 사용자 간의 관계를 도출한다.
\[ \tilde{S} [u, k] = \text{ReLU} ( h^{\top} \text{ReLU} ( W_2 concat ( [ s^u_{T+1}, s^k_T ] ) + b_2 ))) \]
$\tilde{S}[u, k]$는 $k$ 명의 이웃과 $u$ 간의 유사도 정보를 담고있는 행렬을 의미한다. 그런 다음 $k_2$개 만큼의 이웃을 추출해 $\tilde{N}_u$를 생성하고, 이를 바탕으로 인접 행렬 $\tilde{A}[u, k^{\prime}]$를 구성한다.
\[ \tilde{N}_u = \text{argtop}_{k_2} ( \tilde{S} [u, :] ) \]
\[ \tilde{A}[u, k^{\prime}] = \begin{cases} Softmax ( \tilde{S} [u, k^{\prime}]), & k^{\prime} \in \tilde{N}_u \\ \\ 0, & \text{Otherwise} \end{cases} \]
Attentive Interest Propagation Layer
최종적으로 Graph Convolution Layer를 통과하여 각 사용자에 대한 Embedding을 도출할 수 있다.
\[ P^{(l)}_{tar} = \text{ReLU} ( (\tilde{A} P_{src} + P^{(l-1)}_{tar} ) W^{(l)} ) \]
$P_{src}$와 $P_{tar}$는 Dynamic Interest Modeling 단계의 Long-term Interest에서 도출한 $p_{src}$와 $p_{tar}$를 행렬 형태로 변환한 값을 의미한다.
Recommending
마지막 단계는 최종 $p^u_{final}$을 도출한 후 각 제품에 대한 확률값을 도출하는 단계다. 이번 단계에서는 Skip-Connection 기법을 적용해 아래와 같이 최종 Embedding을 도출하고, Softmax Function을 사용해 각 제품에 대한 확률값을 도출한다.
\[ p^u_{final} = p^u_{tar} + p^{u(l)}_{tar} \]
\[ \begin{equation} \begin{split} & \text{Prob} ( y | i^u_{T+1, 1}, i^u_{T+1, 2}, \cdots, i^u_{T+1, m} ; \{ S^k_T, k \in \tilde{N}_u \} ) \\ \\ & = \frac{\exp ( z^{\top}_y p^u_{final}) }{\sum^{|\mathcal{I}|}_{j=1} \exp (z^{\top}_j p^u_{final} )} \end{split} \end{equation} \]
$z_y$는 y번째 제품 Embedding을 의미한다.
Parameter Learning
Overall Learning Objective
본 연구에서는 Two-stage 방식을 제안하였기 때문에, Coarse Neighbor Screening을 위한 Loss Function과 Self-adaptive Graph Structure Learning을 위한 Loss Function이 필요하다. 수식은 다음과 같이 정의된다.
\[ \mathcal{L}_{rec} = \sum_{u \in \mathcal{U}} \sum^T_{t=1} \log \text{Prob} (i^u_{t+1, m+1} | i^u_{t+1, 1}, \cdots, i^u_{t+1, m}; \{S^k_t, k \in \tilde{N}_u \}) \]
\[ \mathcal{L}_{scr} = \sum_{u \in \mathcal{U}} \sum_{i \in \tilde{N}_u} \sum_{j \in (\mathcal{U} - \tilde{N}_u)} -\log (\sigma ( S[u, i] - S[u,j])) + \lambda S[u, j]^2 \]
$S[u, j]$는 Negative User Pair를 의미한다.
Phased Heuristic Learning Strategy
본 연구에서는 모델의 유효성을 위해 Heuristic Learning 전략을 사용한다고 언급했다. 처음 학습할 때 Embedding의 값을 무작위로 설정하고 학습하고 있으나, 본 연구에서는 Warm Up Start를 통해 학습을 수행한다.
\[ \epsilon = \frac{r}{r + \exp (\frac{step}{r} )} \]
$r$은 Hyper-parameter로 조절이 가능하다. $Step$은 최근 학습 Step을 의미한다. (Figure 3)

Experiments
본 연구에서 제안하는 GCL4Rec의 성능을 검증하기 위해 Delicious, Yelp, Lthing, Dianping, Mind 데이터를 바탕으로 실험을 진행하였으며, BPR-MF, SBPR, SoReg, GRU4Rec, NARM, DGRec, DREAM 등의 기법을 베이스라인 모델로 선정하여 비교분석하였다.
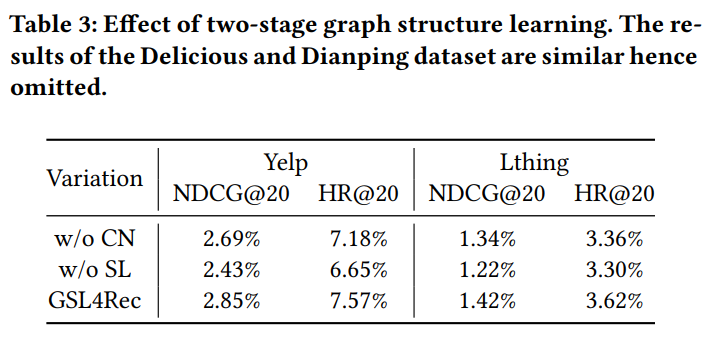
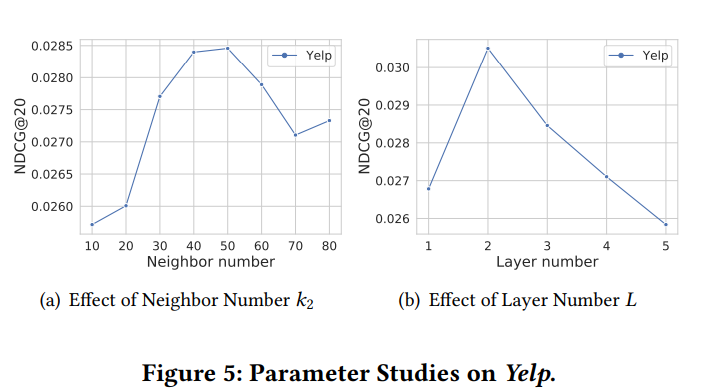
본 연구의 실험은 1) Performance Comparison, 2) Ablation Study, 3) Parameter Sensitive Study 로 구성되어 있으며, Perormance Comparison은 베이스라인 기법들과 성능을 비교 분석하는 실험이다 (Table 2). Ablation Study는 Coarse Neighbor, Self-adaptive Graph Structure Learning 등과 같은 GSL4Rec 모델 내에 존재하는 Stage를 제거하여 성능 차이를 비교분석하는 실험이다 (Table 3, Figure 4). 마지막으로 Parameter Sensitive Study는 Number of $k_2$, Number of Layer 등과 같은 세부적인 파라미터에 따른 추천 성능을 비교분석 한 실험이다 (Figure 5).