해당 논문은 CIKM'23 에서 주재걸 교수님과 SK Telecom 팀이 발표한 논문이다. 논문에서 알 수 있다시피, Negative Transfer를 줄이기 위한 연구이며, 이때 Cooperative Game Theoretic 접근법을 사용한다. Cross-Domain이기 때문에 유저는 중복되지만, 제품은 중복되지 않은 도메인에서 전이학습을 효과적으로 하기 위한 연구라고 볼 수 있다.
Abstract
이 논문에서는 Cross-Domain Sequential Recommendation (CDSR)에 대해서 다루고 있으며, CDSR는 두 개 혹은 세 개 이상의 도메인에서 생성되는 정보를 활용하는 방법이라고 볼 수 있다. 그러나, 서로 다른 도메인 간의 Negative Transfer이 발생해 오히려 성능 저하가 발생할 수 있다. 본 논문에서는 Cooperative Game Theory를 통해 Negative Transfer 문제를 해결할 수 있는 새로운 CDSR Framework를 제안한다. 또한, Coarse-Level의 정보와 Fine-Level의 정보를 통합할 수 있는 Hierarchical Contrastive Learning 방식을 이용해 Negative Transfer의 영향을 완화한다.
Introduction
추천 시스템에서 사용자의 선호도를 측정하는 방식은 특정 도메인 내에 존재하는 데이터를 사용하는 것이 일반적이다. 이와 같은 방식은 단일 도메인에서 수집된 데이터만 사용하기 때문에 편향된 추천 결과를 만들 수 있다. 이와 같은 문제를 해결하기 위해 CDSR 기법이 제안되었다. CDSR는 다른 도메인의 정보를 활용하여 여러 도메인의 추천 성능을 향상시키는 것을 목표로 하고 있다. 사용자 상호작용에서의 순차적 특징을 추출해 시간이 지남에 따라 변화하는 사용자의 선호도를 잘 이해할 수 있기 때문이다.
그러나, CD 의 경우 서로 다른 도메인에 대한 정보를 바탕으로 정보를 주고 받으면서 Negative Transfer 문제가 발생한다. 이때 Negative Transfer의 영향으로 인해 오히려 성능이 저하될 수 있다. [Figure 1 참조]

Figure 1에서 볼 수 있듯, Book 도메인에 데이터와 Movies, Sports, Clothings, Toys 등의 데이터를 통해 Cross Domain 방식으로 CDSR를 수행했을 때 Book 도메인의 경우 Movies와 함께 사용한 경우 사용자가 비슷한 선호도를 띄는 제품을 좋아하기 때문에 추천 성능이 향상된 것을 확인할 수 있으나, Sports와 같은 도메인에서는 서로 다른 선호도를 가질 수 있기 때문에 성능이 많이 저하된 것을 볼 수 있다.
이러한 Negative Transfer 문제를 완화하기 위해 기존 연구에서는 Global-specific, Domain-specific 사용자 정보를 모두 활용해서 학습을 진행했으나, 시간에 따라 Negative Transfer의 영향이 달라질 수 있음에도 불구하고, 두 도메인 간의 Sequential 정보는 고려하지 않았다.
본 논문에서는 시간적인 정보까지 함께 고려하는 Cooperative Game Theoretic Approach for Cross-Domain Sequential Recommendation (CGRec)을 제안한다. CGRec은 부정적인 영향을 주는 요소를 완화함으로써 성능을 개선시켰으며, 기존 연구에서와는 달리 3개 이상의 도메인을 융합한 실험을 진행하였다.

Figure 2를 참고하면, CGRec은 이처럼 서로 다른 도메인 간의 시간 순서까지 고려하여 제품 간의 정보를 효과적으로 추출한다는 것이다. 예를 들어, BBQ USA 같은 Outdoor Cooking 카테고리의 제품을 구매한 사용자가, Hunting & Fishing 카테고리의 낚시 루어 제품을 구매하면 이는 관계 있다고 볼 수 있기 때문이다.
Related Work
Related Work은 1) Sequential Recommendation, 2) Cross-Domain Recommendation, 3) Cross-Domain Sequential Recommendation 총 3 개의 Section으로 나누어 정리하였다. 이번 글에서는 개략적인 부분만 짚고 넘어가는 형식으로 진행하고자 한다.
Sequential Recommendation
Sequential Recommendation은 시간 순서에 따라 변화하는 사용자의 선호도를 파악하기 위해 제안된 기술이며, 대표적인 모델로는 GRU4Rec, SASRec, BERT4Rec 등의 모델이 있고, 추가적인 정보를 활용한 S
Cross-Domain Recommendation
Cross-Domain Recommendation (CDR) 는 타겟(Target) 도메인에서 다른 도메인의 정보를 활용해 추천 성능을 향상시키는 것을 목적으로 두고 있다. 대표적인 모델로는 CMF, CLFM, DTCDR, BiTGCF, DeepAPF, CDR, CAT-ART 등의 모델이 있다. 그러나 CDR 관련 모델들도 다른 도메인 간의 내재된 순차적인 정보를 고려하지 않았다.
Cross-Domain Sequential Recommendation
CDSR 기법의 목적은 다른 도메인을 활용해 Sequential Recommendation Task의 성능을 향상시키는 것이다. 대표적인 모델로는
Preliminary
본 논문에서는 CDSR 기법을 확장하는 것이 목적이다.
Definition 1. Hierarchical Categories of Items
각 Item 은 다양한 카테고리에 속할 수 있으며, 각 도메인 내 H-Level 계층적 분류를 가정하고 있다. 계층적 구조에서 Level 1은 가장 Coarsest-Grained 카테고리고, Level H는 Finest Category로 지정한다. 다시 말해, Level 1에서 Level H로 갈수록 점점 더 세분화되는 카테고리라고 보면 된다.
Definition 2. Domain-hybrid Sequence
Domain
Problem Statement
CDSR에서 t 시점까지의 domain-hybrid Sequence가 주어지면,

Model
CGRec은 Item Embedding Layer, Self-Attention Encoder, Hierarchical Prediction Layer, Loss Re-Balancing Layer로 구성되어 있으며, 마지막 Loss Re-Balancing Layer에서 Cooperative Games를 이용한 Negative Transfer를 감소시키는 역할을 담당한다.
Item Embedding Layer
Category Sequence는 Item Sequence보다 일반적인 사용자의 선호도를 나타내기 때문에, 관련 없는 도메인에서의 전달되는 Negative Transfer의 영향을 완화시킨다. 첫 번째로는, 각각의 Domain-hybrid Sequence를 고정된 길이
그 다음으로는, Domain-hybrid Sequence
그 다음으로는, Domain의 모든 level-
결과적으로, 최종 Sequence Representation
Self-Attention Encoder
Self-Attention Layer는 기존 Self Attention과 별반 다를 것 없는 구조를 가지고 있으며, 본 논문에서는 Multi-head Self-Attention 에 Scaled dot-product, 그리고 마지막으로 Point-Wise Feed-Forward Network를 사용하였다.
Hierarchical Prediction Layer
Hierarchical Prediction Layer는 Item Level의 영향을 줄여 Negative Transfer를 예방하기 위한 목적으로 사용된다. Coarse-grained 부터 Fine-grained 까지 분리하여 계층적으로 학습한다.
그런 다음 Level 2에 대해서 순차적으로 진행하고, 최종적으로 H 카테고리까지 이 방식을 계속 반복한다.
Training Objective
본 연구에서는 기존 연구를 참고하여 Hierarchical Conatrastive Learning을 사용하여 학습을 진행했다. 첫 번째 카테고리 즉, Coarsest Categories 부터 입력으로 들어가서 다음, Finer-Grained Categories를 예측하는 식으로 학습하기 때문에 아래와 같은 목적 함수를 설정할 수 있다.
Loss Re-balancing Layer
CGRec은 Negative Transfer를 줄이는 것이 목적이다. 본 논문에서는 Negative Transfer과 Marginal Contribution 두 개의 값을 서로 반대되는 컨셉으로 설정하고, 이를 기반으로 Cooperative Game 이론을 적용하였다. Cooperative Game 이론을 간략하게 설명하면, 더 많은 기여를 한 사람에게 더 많은 리워드를 제공하는 이론으로 이해하면 된다. Loss Re-balancing Layer에 대해 설명하기 이전에, Cooperative Game과 Shapley Value에 대해서 알아보자.
Cooperative Game
이때 Cooperative Game은
Shapley Value
샤플리 값 (Shapley Value)는 모든 연합의 누적 보상을 골고루 공평하게 분배하는 접근 방식을 의미한다. 샤플리는 구성원이 될 수 있는 모든 잠재 연합에 대한 Marginal Contribution을 계산하여, 각 플레이어에 대해 평가하는 방법을 제안하였으며, 아래와 같은 수식으로 계산된다.
Quantifying Negative Transfer of Each Domain
본 연구에서는 위에서 설명한 플레이어
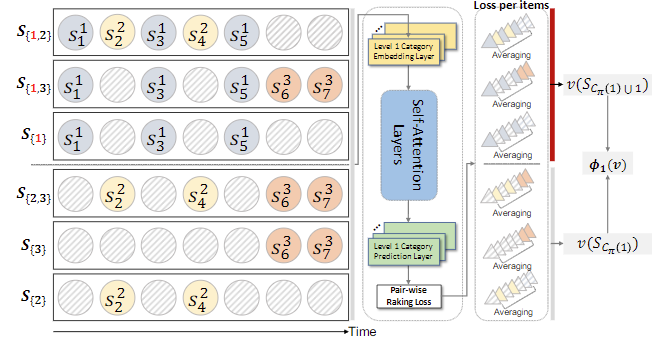
Figure 4를 살펴보면, 1을 뺀 집합과 2을 포함한 집합 간의 값을 계산하는 것을 확인할 수 있다.
그런 다음, Negative Transfer의 Relative Value를 계산하게 된다.
Loss Re-balancing
위에서 계산된
위 수식을 최소화하는 방식으로 학습한다. 이때
Experiments
본 연구에서는 총 3가지 질문에 답변을 하는 식으로 기술하고 있다. 첫 번째(RQ 1), CGRec이 SoTA 모델들보다 우수한가? 두 번째(RQ 2), CGRec 을 사용할 때 Negative Transfer를 완화할 수 있는가? 세 번째(RQ 3), CGRec 모델 내 각각의 모듈들이 성능에 어떠한 영향을 미치는가?
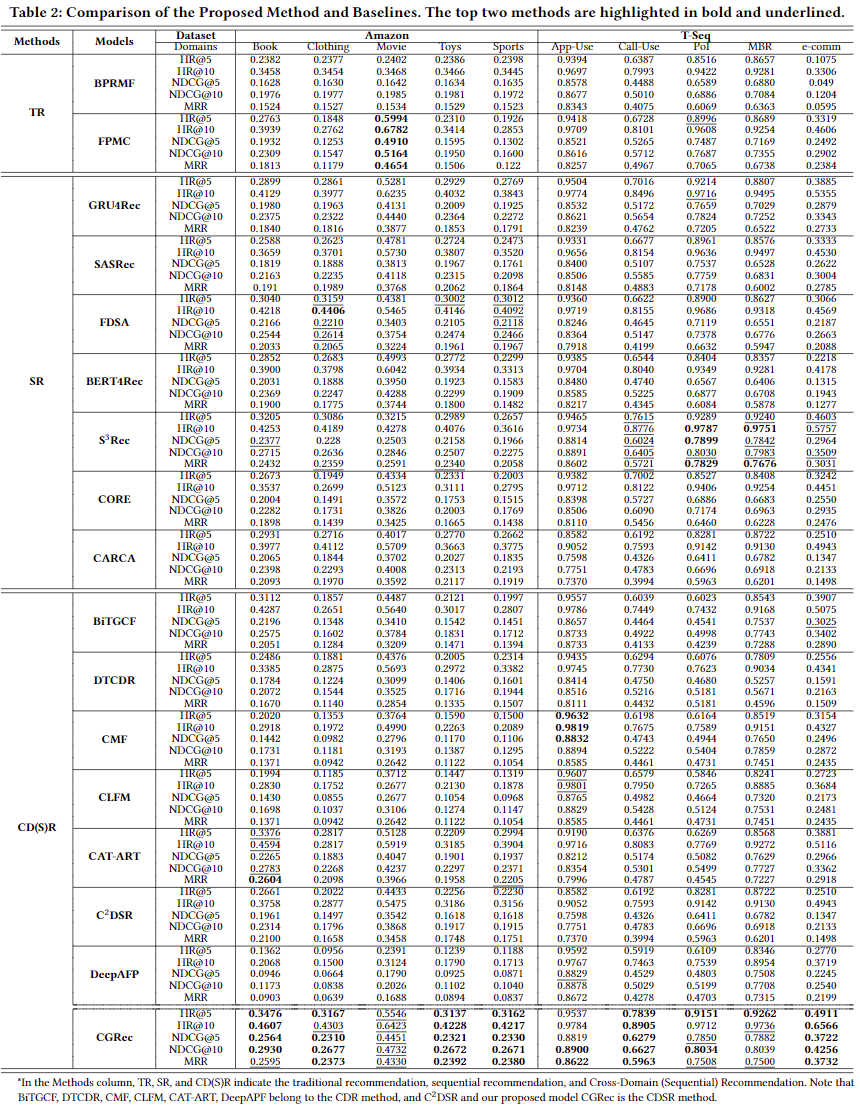
Dataset은 Amazon 데이터와 T-Seq 데이터를 사용하였으며, 평가 지표는 NDCG@{5, 10}, MRR, HR@{5, 10} 을 사용하였고, 베이스라인 모델은 Tradictional Recommendation (TR), Sequential Recommendation (SR), Cross-Domain Sequential Recommendation (CD(S)R) 을 사용하였다. 성능에 대한 부분은 Table 2를 참고하면 된다.
RQ 1
본 논문은 연구에 대해 세부적으로 많은 내용을 다루었다. Figure 5를 살펴보면 Book과 Movie에 대해서는 매우 우수한 성능을 보이는 것을 볼 수 있다. 그러나, Sports와 Clothing을 살펴보면 Negative Transfer의 영향이 엄청나게 큰 것을 확인할 수 있다.
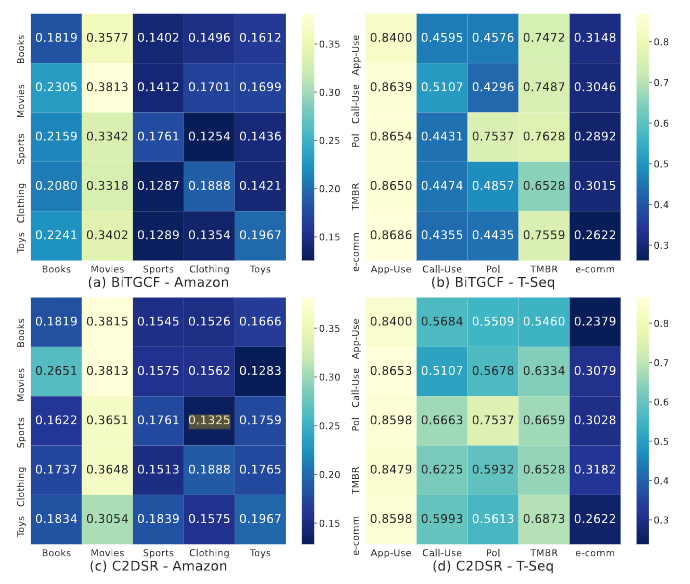
RQ 2
Table 3는 베이스라인 모델의 평균과 본 논문에서 제안하는 CGRec 간의 성능을 비교하였다. 베이스라인 모델은 Clothing, Sports와 같은 도메인에서 오히려 성능이 많이 저하되는 것을 볼 수 있는데, 본 논문은 베이스라인 모델과는 달리 Sports, Clothing 부분에서도 다른 베이스라인 모델에 비해 더 많은 성능 개선을 보여준 것을 확인할 수 있다. 이를 통해 본 논문에서 제안하는 모듈들이 Negative Transfer의 영향을 줄일 수 있다는 것이 확인되었다.
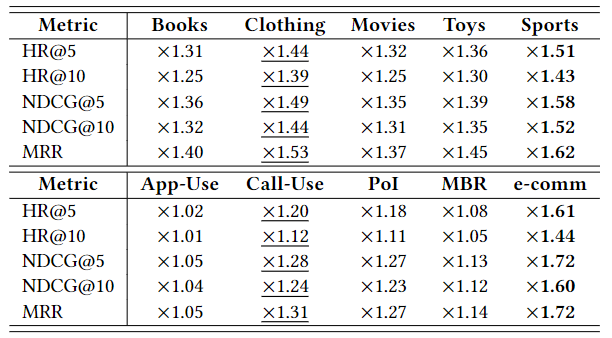
RQ 3
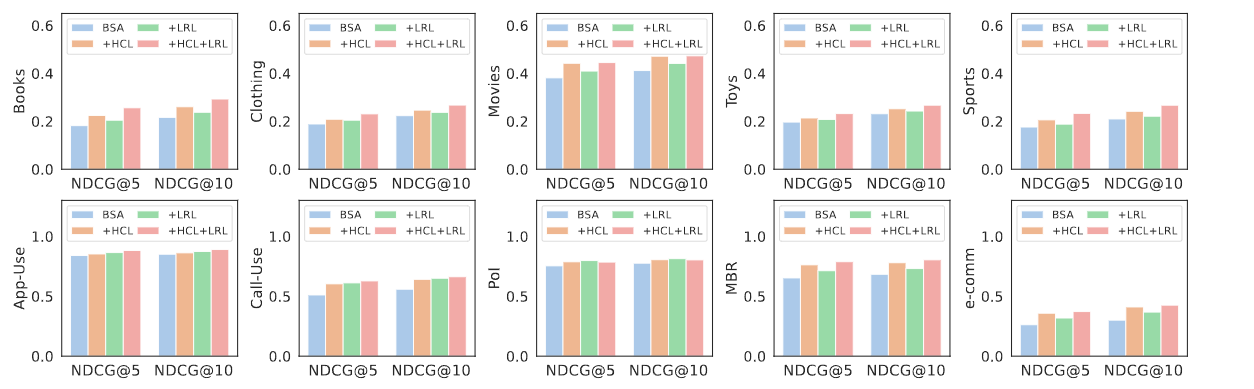
RQ 3는 CGRec 안에 모듈들이 각각 성능에 어떤 영향을 미치는지 확인하는 Ablation Study로 볼 수 있다. (1) Basic Self-Attention model (BSA), (2) + Hierarchical Contrastive Learning (HCL), (3) + Loss Re-balancing Layer (LRL) 으로 총 3개의 모듈이 존재하며 기본 모듈에 (2), (2), (2,3)을 적용했을 때 어떤 차이가 있는지 실험하였다.
아래의 그림에서도 확인할 수 있듯, HCL, LRL 두개를 사용했을 때 모두 성능이 좋은 것을 확인할 수 있었고, 도메인에 따라 각 모듈의 영향력의 차이가 어느정도 존재하지만, 일반적으로 HGL 의 영향이 LRL의 영향력에 비해 조금 더 큰 것을 확인할 수 있다.