Contents
본 연구에서는 Self-supervised Learning을 적용한 Model-agnostic 기법인 CL4CTR 기법을 제안한다. CL4CTR 기법은 Contrastive Loss, Feature Alignment, Field Uniformity로 구성되어 있다.
Introduction
CTR Prediction Task는 제품이 클릭될 확률을 계산하는 Task로 널리 사용되는 Task 중 하나이다. 기존 CTR Prediction의 경우 크게 두 가지로 나눌 수 있다. 1) Traditional Methods (such as Logistic Regression, Factorization Model), 2) Deep-learning Based Methods (such as xDeepFM, DCN-V2). Traditional Methods와 Deep-learning Based Methods는 성능이 우수한 것이 검증되었으나 많이 등장하는 Feature가 적게 등장하는 Feature에 비해 더 많이 학습될 기회를 얻는다. 다시 말해, 많이 등장하는 Feature는 자주 등장하기 때문에 학습이 잘되지만, Long Tail에 존재하는 Feature는 상대적으로 적은 학습이 이루어진다. Figure 1(b)를 살펴보면 80%의 Feature가 38번 등장하거나, 더 적은 것을 볼 수 있다.

일부 연구에서 위 문제를 해결하기 위해 각 Feature에 대해 Weight를 주는 모델을 제안하였으나, 이와 같은 모델은 Inference 단계에서 Model Parameter를 증가시키는 문제가 존재한다. 따라서, 본 연구에서는 이와 같은 문제를 해결하고자, Self-supervised Learning (SSL)을 활용한 Contrastive Learning for Click Through Rate (CL4CTR) 기법을 제안한다.

Figure 2를 간단히 살펴보면 CL4CTR 기법은 CTR Prediction Model, Contrastive Module, Alignment&Uniformity Constraints 으로 구성되어 있다.
The CL4CTR Framework
CTR Prediction
CTR Prediction Model은 Binary Classification Task로, N개의 Instance $(x, y)$에서 $y \in \{0, 1\}$을 예측하는 형태다. $x$는 주로 Table 1과 같이 Multi-Field로 구성되어 있다. 본 연구에서 사용하는 CTR Prediction은 총 4단계로 구성된다. 1) Embedding Layer, 2) Feature Interaction Layer, 3) Prediction Layer, 4) Contrastive Learning.
먼저 Embedding Layer는 $(x, y)$를 입력으로 받아, $x$를 Low-dimensional Embedding Vector로 Embedding 하는 단계다. 즉, $E = [e^1, e^2, \cdots, e^F] \in \mathbb{R}^{F \times D}$로 변환하는 것이다. 이때 D는 차원의 크기를 의미하고, F는 Feature의 수를 의미한다. 모든 입력에 대한 Feature Embedding Vector를 행렬로 표현하면, $ \mathbb{E} = [E_1, E_2, \cdots, E_F] \in \mathbb{R}^{M \times D}$가 된다.
Feature Interaction (FI) Layer는 MLP, Transformer 등과 같은 기법을 통해 Compact Feature Representation $h_i$를 출력하는 단계다. 이렇게 출력된 $h_i$를 Prediction Layer에서 아래와 같은 Loss Function을 이용해 최적화한다.
\[ \mathcal{L}_{ctr} = \frac{1}{N} \sum^N_{i=1} (y_i \log ( \sigma (\hat{y}_i ) ) | (1 + y_i) \log (1 - \sigma (\hat{y}_i ) ) \]
위 전체적인 구성에 Contrastive Learning을 적용한 것이 본 연구의 핵심이기 때문에, Contrastive Learning Layer가 추가된다. 본 연구에서 사용하는 Contrastive Learning은 Contrastive Loss, Feature Alignment Constraint and Field Uniformity로 구성되어 있다.
Contrastive Module
이번 단계는 Figure 2(b)에 해당하는 단계이며, Data Augmentation, FI Encoder, Contrastive Loss Function으로 이루어져 있다. Data Augmentation 단계는 Random Mask, Feature Mask, Dimension Mask로 구성되어 있으며, 아래의 수식과 같이 계산된다.
\[ \text{Random Mask} = \hat{E} = g_r (E) = E \cdot I, \quad I \sim \text{Bernoulli}(p) \in \mathbb{E}^{F \times D} \]
\[ \text{Feature Mask} = \hat{E} = g_f (E) = [\hat{e}^1 ; \hat{e}^2 ; \cdots ; \hat{e}^F ], \quad \hat{e}^f = \begin{cases} e^f, & t \notin \mathcal{T} \\ \\ [mask], & t \in \mathcal{T} \end{cases} \]
\[ \text{Dimension Mask} = \hat{E} = g_d (E) = [de^1; de^2; \cdots ; de^F ], \quad d \sim \text{Bernoulli} (p) \in \mathbb{R}^D \]
Feature Interaction (FI) Encoder는 이전 단계에서 생성된 두 개의 Perturbed Embeddings $\hat{E}_1$, $\hat{E}_2$를 각각 아래와 같은 함수를 통해 계산하여 $h_1$, $h_2$를 도출한다.
\[ h_1 = FI_{cl} (\hat{E}_1), \quad h_2 = FI_{cl} (\hat{E}_2) \]
$FI_{cl}(\cdot)$는 FI Encoder Function을 의미하고, $h_1$, $h_2$는 각각의 Perturbed Embeddings에서 계산된 Representation을 의미한다. 그런 다음 Projection Function $p(\cdot)$을 사용하여 $\hat{h}$를 도출한다. 이때 $p(\cdot)$는 Single Layer MLP를 사용한다.
\[ \hat{h}_1 = p_1 (h_1), \quad \hat{h}_2 = p_2 (h_2) \]
마지막 단계는 Contrastive Loss Function 단계다. 이번 단계는 $\hat{h}_1$과 $\hat{h}_2$ 간의 차이를 최소화 하기 위한 Loss Function으로 보면 된다.
\[ \mathcal{L}_{cl} = \frac{1}{B} \sum^B_{i=1} || \hat{h}_{i, 1} - \hat{h}_{i, 2} ||^2_2 \]
$B$는 Batch Size를 의미하고, $|| \cdot ||^2_2$는 $l_2$ Distance를 의미한다.
Feature Alignment and Field Uniformity
이번 단계에서는 Low Frequency와 High Frequency의 동일한 학습을 하도록 하기 위한 가장 간단한 방법은 Low Frequency를 Up Sampling하거나 High Frequency를 Down Sampling하는 방식이다. 본 연구에서는 기존 선행 연구를 참고하여 Feature Alignment 방식과 Field Uniformity 방식을 사용한다. 먼저 Feature Alignment 방식의 수식은 다음과 같다.
\[ \mathcal{L}_a = \sum^F_{f=1} \sum_{e_i, e_j \in E_f} ||e_i - e_j ||^2_2 \]
$c_i$와 $c_j$는 같은 Field 에 있는 Feature를 의미한다.
Field Uniformity는 두 Feature간의 유사도를 최소화하는 방식으로 학습하며 아래의 수식과 같이 계산된다.
\[ \mathcal{L}_u = \underset{1 \le f \le F}{\sum_{e_i \in E_f}} \sum_{e_j \in ( \mathbb{E} - E_f)} sim(e_i, e_j) \]
$sim(c_i, c_j)$는 Cosine 유사도를 사용하였으며, $\mathbb{E} - E_f$는 Field $f$를 뺀 나머지 Field를 의미한다.
Multi-task Training
위 과정을 통해 도출된 각 단계의 Loss를 종합하여 정리하면 CL4CTR 기법의 최종 Loss Function을 아래와 같이 정의할 수 있다.
\[ \mathcal{L}_{total} = \mathcal{L}_{ctr} + \alpha \cdot \mathcal{L}_{cl} + \beta \cdot ( \mathcal{L}_a + \mathcal{L}_u ) \]
Experiments
본 연구에서는 Frappe, ML-tag, SafeDriver, ML-1M 등과 같은 Public Dataset을 사용해 실험을 진행하였으며, 베이스라인 모델은 LR, FM, FwFM, IFM, FmFM, CrossNet, IPNN, OPNN, FINT. DCAP, WDL, DCN., DeepFM, xDeepFM, FiBiNet, AutoInt+, AFN+, TFNET+, FED+, DCN-V2 등과 같이 다양한 기법을 사용하였다.
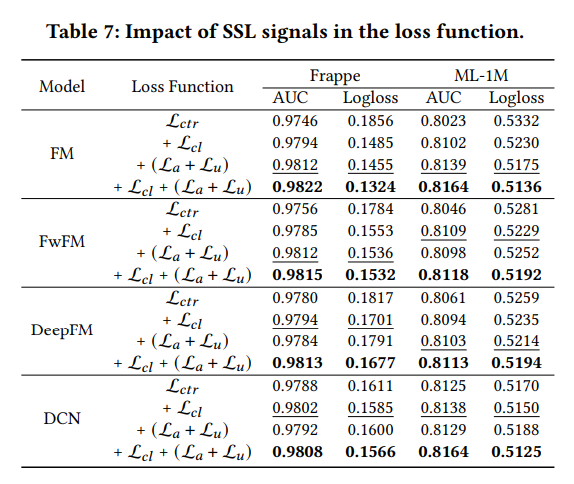
실험은 Overall Comparison, Ablation Study, Feature Frequency Analysis, Hyper-parameter Analysis로 총 4 가지로 구성하였다. 먼저 1) Overall Compasion의 경우 전체적인 베이스라인 기법과 CL4CTR 기법 간의 성능을 비교하는 실험이다 (Table 3). 2) Ablation Study는 CL4CTR 기법에 존재하는 Contrastive Module, Alignment & Uniformity Constraints, FI Encoder, Loss Function 등과 같은 단계를 제거했을 때 어떤 성능 변화가 존재하는 지를 다룬 실험이다 (Table 4 ~ 7). 3) Frequency Analysis는 Low Frequency 와 High Frequency에 존재하는 제품들이 골고루 학습에 사용되었는지에 대한 것을 다룬 실험이다 (Figure 3). 마지막 4) Hyper-parameter Analysis는 Model Sensitivity를 알아보는 실험으로, $\alpha$, $\beta$, Mask Proportion 등과 같은 Hyper-parameter의 비율을 달리 설정했을 때 어떤 성능 변화가 존재하는지를 알아보는 실험이다 (Figure 4 ~ 6).