Contents
해당 논문은 SIGIR'22 6월에 발표된 논문이다. 제목에서도 알 수 있듯 리뷰를 사용하여 추천 시스템을 구축하고자 하는데, Graph Mining과 Contrastive Learning을 사용하는 것으로 보인다. Contrastive Learning은 대조학습으로 최근 Data augmentation 관점으로 추천 시스템이 가지고 있는 Sparsity 문제를 완화하기 위해 주로 사용되곤 한다.
Introduction
추천 시스템에서는 Sparsity 문제 즉, Cold Start 문제를 해결하기 위해 리뷰를 사용하여 사용자가 선호할 만한 제품을 추천하기 위한 연구를 진행하고 있다. 예를 들어, 사용자가 한 리뷰에 대해서 평점을 부여한 경우 하나의 평점으로 사용자의 선호도를 예측하는 것은 상당히 어려운 문제가 된다. 반면에, 사용자가 하나의 제품에 리뷰를 남긴 경우 리뷰 내에서 사용자의 선호도를 유추하는 것은 상대적으로 쉽다. 따라서, 적은 리뷰를 가지고도 사용자에게 제품을 추천할 수 있기 때문에 Cold Start 문제가 완화된다.
일반적으로 사용자와 제품의 리뷰를 계산하여 더 좋은 user, item embedding을 생성하기 위해 사용하거나, user-item 리뷰를 이용하여 user-item intraction 모델링을 하기 위해 사용한다. 전자의 경우 과거 리뷰를 보조적인 지표로 활용하며, 대표적인 모델로는 DeepCoNN, FM(Factorization Machine) 등이 있다. 그러나 이 경우 과거 사용자의 리뷰는 스타일, 가격 등 다양한 속성들이 너무 세분화되어 있어서 활용하는 것이 어렵다. 따라서, 전자의 문제점을 해결하고자 user-item interaction 모델링 방법이 제안되었다. 본 논문에서는 전자에서 사용한 방법과 차이를 두기 위해 해당 방법을 target review로 작명하였으며, target review에 남겨진 평점 정보는 target rating으로 명명하였다. target review 방식은 이전 방법과 달리 training 단계에 존재하는 사용자의 user-item pair는 활용할 수 있으나 inference 단계에서는 활용할 수 없다. 따라서, inference 단계에서 학습을 용이하기 위해 학습 과정에 사용이 가능한 리뷰를 전달하는 방법인 TransNets 등의 모델을 제안하였다.
해당 모델들은 우수한 성능을 발휘함에도 불구하고 다음과 같은 문제점이 존재한다. 1) user-item 관계는 일반적으로 bipartite graph를 형성하고 있기 때문에, unique한 그래프의 구조를 고려하여 추천하는 것이 어렵다. 2) 제한된 사용자의 행동으로 인해 embedding을 학습하거나 user-item interaction 모델링을 하는 것이 어렵다. 즉, 사용자가 모든 제품에 대해서 리뷰를 작성하는 것이 아니기 때문에 여전히 sparsity 문제가 존재한다는 것을 의미한다.
본 논문에서는 이와 같은 문제를 해결하고자 Review-aware Graph Contrastive Learning (RGCL)을 제안한다. RGCL은 더 좋은 추천을 위해 Contrastive Learning을 이용하여 리뷰 정보를 보다 효율적으로 활용하는 방식이다. 먼저 RG (Review aware Graph) 방식은 user-item bipairtite graph의 구조를 보다 효과적으로 포착할 수 있고, CL (Contrastive Learning)은 embedding 학습과 user-item interaction 모델링 프로세스의 성능을 향상시킨다. 구체적으로 ND (Node Discrimination)과 ED (Edge Discrimination)를 제안한다.
Related Work
본 논문에서는 과거 리뷰를 활용하는 추천 시스템 관련 논문과 target reivew를 활용하는 논문 마지막으로 Contrastive Learning을 활용한 논문으로 구성해서 관련 연구를 정리하였다. 과거 리뷰를 활용하는 논문 중 대표적인 모델은 LDA, DeepCoNN이 있고, target review를 활용하는 논문은 DualPC, DRRNN 등이 있다. 마지막으로 Contrastive Learning을 활용한 논문은 GRACE, DGI 등이 있다.
추가적으로 추천 시스템에서 Contrastive Learning을 활용하는 논문은 SGC, SimGCL 등의 논문도 있으니 함께 참고해서 Contrastive Learning이 왜 추천 시스템에서 사용되는지 한 번 알아보면 많이 도움이 된다. 본 블로그에서 Graph 관련 논문 리뷰에도 Contrastive Learning을 활용한 추천 시스템 논문의 리뷰가 있으니 참고하길 바란다.
Problem Definition
본 논문에서 사용하는 기호들에 대해서 알아보자.
- $\mathcal{U}(\mathcal{U} = M)$: a user set
- $\mathcal{V}(\mathcal{V} = N)$: a item set
- $u_i \in \mathcal{U}$ and $v_j \in \mathcal{V}$.
- $M$: the number of users
- $N$: the number of items
- $\boldsymbol{R} \in \mathcal{R}^{M \times N}$: user-item rating matrix
- $\mathcal{R} = \{1, 2, 3, 4, 5 \} $: the set of all ratings.
- $e_{ij} \in \mathbb{R}^d$: a fixed-size vector as the representation
- $\boldsymbol{E} \in \mathbb{R}^{ M \times N \times d}$: review features of all interactions
- $\mathcal{E}=\{R, E \}$: user-item interaction
- $\mathcal{G}$: graph
- $\hat{\boldsymbol{R}} \in \mathcal{R}^{M \times N}$: final rating matrix (prediction)
Review-aware Graph Contrastive Learning
본 논문에서 제안하는 RGCL은 RG와 CL로 구성되어 있다. RG는 Review-aware Graph 를 의미하고, CL은 Contrastive Learning을 의미한다. RG에서는 리뷰를 통해서 가중치를 계산하고, CL에서는 Data Augmentation 관점으로 접근한다. 각 모듈에 대해서 상세히 알아보자.

Review-aware Graph Learning Module
먼저 각 user, item embedding을 초기화한다. 그 후 BERT-Whitening 방법을 사용하여 리뷰에 대한 $e_{ij}$를 생성한다. 그 다음 Review-aware Message Passing 단계를 수행한다. 첫 번째로는 user, item embedding을 잘 학습하기 위한 보조적인 지표로 활용한다. 두 번째로는 $e_{ij}$를 통해 가중치를 계산한다. 이는 사용자가 제품을 좋아하거나 싫어하는 범위를 학습하는 데 도움이 될 수 있다.
\[ x^{(l)}_{r; j \rightarrow i} = \frac{ \sigma (w^{(l) \top}_{r, 1} e_{ij} ) W^{(l)}_{r, 1} e_{ij} + \sigma ( w^{(l) \top}_{r, 2} e_{ij} ) W^{(l)}_{r, 2} v^{(l-1)}_j }{ \sqrt{ | \mathcal{N}_j | | \mathcal{N}_i } } \]
이때 $ \sigma ( w^{(l) \top}_{r, 1} e_{ij} ) W^{(l)}_{r, 1} e_{ij}$는 embedding을 잘 학습하기 위한 보조적인 정보를 의미하고, $\sigma (w^{(l) \top}_{r, 2} e_{ij} ) W^{(l)}_{r, 2} v^{(l-1)}_j $는 가중치를 계산해서 Message Passing하는 단계를 의미한다. $W^{(l)}_{r,1}$과 $W^{(l)}_{r, 2}$는 $e_{ij}$와 $v_j$를 곱하기 위해 차원을 맞춰주는 역할을 하는 weight matrix를 의미한다. 위 경우는 $ x_{r;j \rightarrow i}$에 대한 계산이며, 아래의 경우는 $x_{r;i \rightarrow j}$에 대한 수식을 나타낸다.
\[ x^{(l)}_{r; i \rightarrow j} = \frac{ \sigma ( w^{(l) \top}_{r, 1} e_{ij} ) W^{(l)}_{r,1} e_{ij} + \sigma ( w^{(l) \top}_{r,2} e_{ij} ) W^{(l)}_{r, 2} u^{(l-1)}_i}{\sqrt{| \mathcal{N}_i | | \mathcal{N}_j }} \]
Mesage Aggregation 단계는 위 Message Passing 단계를 통해서 수집된 정보를 전부 취합하는 단계다. 본 논문에서는 GC-MC 방법과 유사한 방식으로 rating별로 따로 합계를 아래와 같이 계산한다.
\[ u^{(l)}_i = W^{(l)} \sum_{r \in \mathcal{R}} \sum_{k \in N_{i,r}} x^{(l)}_{r;k \rightarrow i}, \quad v^{(l)}_j = W^{(l)} \sum_{r \in \mathcal{R}} \sum_{k \in N_{j, r}} x^{(l)}_{r;k \rightarrow j} \]
$u^{(l)}_i$와 $v^{(l)}_j$는 각각 $l$ 번째 Layer의 embedding을 의미하고, $\mathcal{N}_{i, r}$는 사용자 $i$가 $r$ 평점을 부여한 제품의 집합을 의미한다. 반대로 $\mathcal{N}_{j, r}$는 제품 $j$에 $r$ 평점을 부여한 사용자의 집합을 의미한다. $L$ 번째까지 Layer을 쌓은 후 $\hat{u}_i$와 $\hat{v}_j$를 출력할 수 있을 것이다. 그럼 이를 $\text{MLP}$ Layer를 통과시켜 $h_{ij}$를 생성한 후 Prediction Layer를 통과해 최종적으로 $\hat{r}_{ij}$를 도출한다.
\[ \hat{u}_i = u^{(L)}_i, \quad \hat{v}_j = v^{(L)}_j \]
\[ h_{ij} = \text{MLP} ( [\hat{u}_i, \hat{v}_j ] ) \]
\[ \hat{r}_{ij} = w^{\top} h_{ij} \]
이때 $[ \cdot ]$는 $\text{GELU}$ 함수를 의미한다.
Contrastive Learning Module
본 논문에서는 ND(Node Discrimination)과 ED(Edge Discrimination)을 사용하여 CL을 적용한다고 앞에서 언급했다. CL은 Self-supervised Learning의 한 종류로 positive pair와 negative pair를 통해 모델을 최적화한다. positive pair는 같은 노드를 의미하고, negative pair는 다른 노드를 의미한다. positive pair 끼리는 유사도가 높아지도록 학습하고, negative pair 끼리는 유사도가 작아지도록 학습한다.
\[ \mathcal{L}^{user}_{nd} = - \mathbb{E}_{\mathcal{U}} \left [ \log \left ( F \left ( \hat{u}^1_i, \hat{u}^2_i \right ) \right ) \right ] + \mathbb{E}_{\mathcal{U} \times \mathcal{U}^{\prime}} \left [ \log \left ( F \left ( \hat{u}^1_i, \hat{u}^2_{i^{\prime}} \right ) \right ) \right ] \]
$ i$는 input user를 의미하고, $i^{\prime}$는 $\mathcal{U}^{\prime} = \mathcal{U}$에서 추출한 negative user를 의미한다. positive pair는 다른 sub-graph $\hat{\mathcal{G}}^1$와 $\hat{\mathcal{G}}^2$에서 추출된 $\hat{u}^1_i$와 $\hat{u}^2_i$를 의미한다. 이때 positive pair $(\hat{u}^1_i, \hat{u}^2_i)$는 유사도가 높게 학습하고, negative pair $(\hat{u}^1_i, \hat{u}^2_{i^{\prime}})$는 유사도가 낮아지도록 학습한다. 위 수식은 사용자에 대한 방식이지만, 제품에 대한 방식도 동일한 방식으로 할 수 있고, 최종 Loss는 $\mathcal{L}_{nd} = \mathcal{L}^{user}_{nd} + \mathcal{L}^{item}_{nd}$로 계산된다.
ED의 경우도 마찬가지로 positive pair 끼리는 가깝게, negative pair 끼리는 멀게 학습한다.
\[ \mathcal{L}_{ed} = - \mathbb{E}_{\mathcal{E}} \left [ \log \left ( F \left ( h_{ij}, e_{ij} \right ) \right ) \right ] + \mathbb{E}_{\mathcal{E} \times \mathcal{E}^{\prime} } \left [ \log \left ( F \left ( h_{ij}, e_{i^{\prime} j^{\prime} } \right ) \right ) \right ] \]
추천 시스템의 경우 Link Prediction이기 때문에 $h_{ij}$와 $e_{ij}$를 비교한다.
Model Optimization
본 논문에서는 평점을 예측하기 때문에 MSE를 사용하여 최적화하고 있다.
\[ \mathcal{L}_{main} = \frac{1}{| \mathcal{S} | } \sum_{(i, j) \in \mathcal{S}} (\hat{r}_{ij} - r_{ij} )^2 \]
$\mathcal{S}$는 학습 데이터 셋의 user-item pair를 의미한다. CL Loss의 경우 ED와 ND의 Loss를 합해서 최종 Loss를 계산하기 때문에 아래와 같은 수식으로 표현할 수 있다.
\[ \mathcal{L} = \mathcal{L}_{main} + \alpha \mathcal{L}_{ed} + \beta \mathcal{L}_{nd} \]
Experiments
본 논문에서는 과거 리뷰를 사용하여 사용자와 제품의 Embedding을 효과적으로 학습하기 위한 보조 지표로 사용하는 모델과 target review 방식의 기법 그리고 Graph 기법을 벤치마크 모델로 사용한다.


실험 결과 본 논문에서 제안하는 RGCL의 기법이 가장 성능이 우수한 것을 확인할 수 있다. 단순히 RG 방법만을 사용한 경우 기존 모델과의 성능 차이가 거의 없는 것을 보이고 있으나, CL 기법을 적용한 경우 전체적으로 성능이 향상되었으며, ND, ED 방법을 모두 사용한 경우 가장 성능이 우수한 것을 확인할 수 있다.

본 논문에서는 RGCL 방법을 통해서 Sparse 문제를 완화할 수 있다고 언급하였다. Sparse 비율을 달리하면서 실험을 진해한 결과 RG 방법에 비해 CL 방법을 적용한 경우 MSE의 성능이 더 우수한 것을 확인할 수 있다.

그 다음으로는 RG 모델에 대한 실험을 진행하였다. RG에는 review 정보를 전달하는 구조와 weight를 계산하는 구조로 이루어져 있다. 이때 어떤 부분이 조금 더 모델 성능 개선에 유의미한지 확인하고자 실험을 진행하였다. 실험 결과, 기존 연구에 비해 review와 weight 정보를 모두 고려한 경우 성능이 향상된 것을 확인할 수 있다.
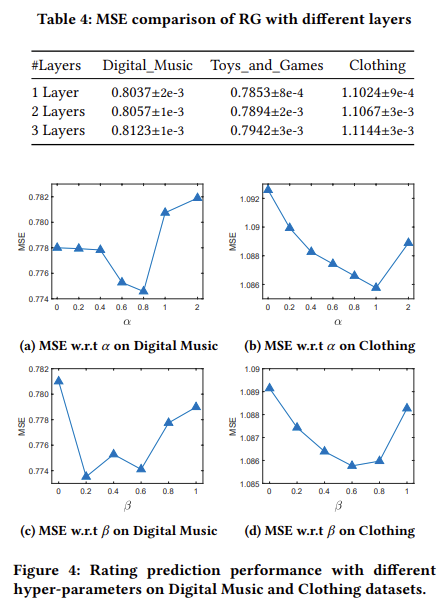
그 다음 실험은 CL Loss의 $\alpha$와 $\beta$에 따른 sensitivity를 측정하였다. $\alpha$의 경우 0.8, 1 지점에서 가장 우수한 성능을 보이고 있으며, $\beta$의 경우 0.2, 0.8 정도에 가장 우수한 것을 확인할 수 있다.

RGCL 기법이 아닌 다른 Graph based 기법에 ED와 ND 등의 기법을 적용한 결과, 다른 기법에 적용한 경우에도 본 논문에서의 CL 기법의 성능이 우수한 것을 확인할 수 있다(Table.5). 마지막 실험은 divergence에 대한 실험이다. 값이 클수록 더 낮은 divergence를 가지는 것을 의미하며, RGCL 일 때의 divergence가 가장 낮은 것을 확인할 수 있다.