[CS231N] 활성화 함수(Activation Fucntion)의 종류

Deep Learning/CS231N

[CS231N] 활성화 함수(Activation Fucntion)의 종류

언킴 2021. 7. 8. 17:24

Training Neural Network

Transfer learning을 진행할 때 고려할 점.

1) Pre-train data와의 이질성

2) Finetuning할 데이터의 양

3) 분석에 할당된 시간

4) 가용한 hardware

...

하나의 layer에서 activation function으로 들어가게 되는데 layer의 값은 $Σ w_{i} x_{i} + b$ 로 선형조합으로 나타낼 수 있다. 그 선형조합을 비선형조합의 activation function으로 넣게 된다. 만약 activation function 자체가 linear라고 생각해보면 layer를 stacking 하는 것 자체가 의미가 없어진다. 왜냐하면 linear function을 activate function으로 사용하게 되면 $i f h (x) = a x$ 가 될 것이고, $h (h (h (x))) = a * a * a * x$ = $a^{4} x$ 와 다를 것이 없기 때문이다. 그렇기 때문에 activation function은 통상적으로 not linear function을 사용하게 된다. (e.g. sigmoid, ReLU, tanh, ...)

일반적으로 tensorflow API에서 Activation function을 제공해준다.

- tf.nn.relu(features, name = None)

- tf.nn.relu6(features, name = None)

- tf.nn.crelu(features, name = None)

- tf.nn.elu(features, name = None)

- tf.nn.softplus(features, name = None)

- tf.nn.softsign(features, name = None)

- tf.nn.dropout(features, noise_shape = None, seed = None, name = None)

- tf.nn.bias_add(features, bias, data_format = None, name = None)

- tf.sigmoid(x, name = None)

- tf.tanh(x, name = None)

Sigmoid

sigmoid는 3가지 문제점을 언급하고 있다. $f (x) = \frac{1}{1 + e^{- x}}$

1) sigmoid의 범위가 [0,1]이기 때문에 그래프의 중심이 0이아니다.

2) safety zone을 넘어가게 되면 gradient가 0이 되어 버린다. $\frac{\partial f}{\partial x} \approx 0$

$x$ = -10 일때 $\frac{\partial f}{\partial x} \approx 0$

$x$ = 0 일때 $\frac{\partial f}{\partial x}$ High rate

$x$ = +10 일때 $\frac{\partial f}{\partial x} \approx 0$

' vanishing gradient problem ' 이 발생할 수 있다.

3) $e$ 함수를 사용하기 때문에 computing하는데 있어서 expensive 한 과정이다.

$e$ 자체가 계산을 하는데에 오래걸린다는 단점이 있다.

tanh

sigmoid의 문제점을 보완하기 위해 도입된 activation function이라고 보면 된다. sigmoid문제 중에서 1번 문제를 해결할 수 있는 그래프이다.

$c o s h (x) = \frac{e^{x} + e^{- x}}{2}$

$s i n h (x) = \frac{e^{x} - e^{- x}}{2}$

$t a n h (x) = \frac{e^{x} - e^{- x}}{e^{x} + e^{- x}}$

하지만 아직도 $e$ function을 사용하기 때문에 계산을 하기 위한 시간이 오래 걸리고, vanishing gradient problem 역시 존재한다.

ReLU ( Rectified Linear Unit )

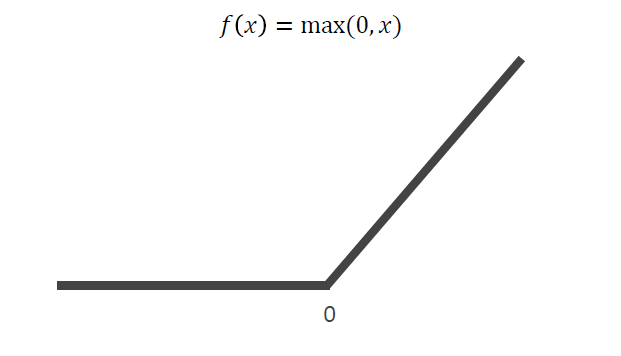
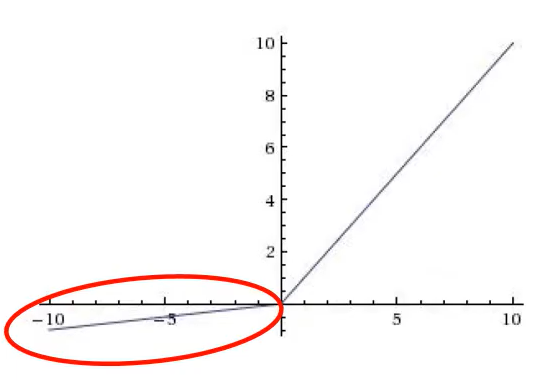
앞선 sigmoid와 tanh와 달리 $e$ function을 사용하지 않고 max function을 사용하기 때문에 굉장히 계산 효율성이 좋다. sigmoid, tanh 보다 6배 빠르다고 한다. ReLU function은 0에서의 좌우 극한이 다르기 때문에 gradient를 구한다는 것이 이상하긴 하지만, 실제 연산에서는 float단위로 연산이 일어나기 때문에 이 부분에 대해서는 크게 신경을 쓰지 않아도 된다고 얘기를 하고 있다.

Leaky ReLU

$f (x) = m a x (0.01 x, x)$

ReLU에서 0인 부분에 $0.01 x$ 의 값을 지정해서 gradient가 0이 되지 않도록 하는 function이다.

Parametic Rectifier ( PReLU )

$f (x) = m a x (α x, x)$

PReLU는 $α$ tern 자체를 backpropagation의 parameter로 집어 넣은 것이다.

$\frac{\partial ε}{\partial a_{i}}$ = $\underset{y_{i}}{Σ} \frac{\partial ε}{\partial f (y_{i})} \frac{\partial f (y_{i})}{\partial a_{i}}$

Exponential Linear Units (ELU)

ELU는 ReLU보다 성능이 좋고, gradient가 0 이되지 않고, output의 평균이 0 이 될 수 있는 등 여러가지 장점들이 있지만 다시 $e$ function이 들어가기 때문에 계산 복잡도가 증가하여 계산하는 부분에서 좋지 않은 부분을 나타낸다.

Q. 만약 우리가 $w$ 자체를 모두 0으로 두거나 어떠한 상수로 전부 동일하게 설정한다면 어떤일이 발생할까?

A. 결론부터 말하자면 좋지 않다. 왜냐하면 backpropagation을 할 때 변화하는 양이 전부다 동일하게 출력된다.

$w$ 를 0.01로 설정했을 경우 .

1. node들의 개수가 많지만 node들의 값이 대부분 0으로 가있기 때문에 가치가 떨어진다.

2. 어떤 값이 있어서 backpropagation으로 계산을 한다 하더라도 gradient에 w를 곱해서 가게 되면서 gradient가 굉장히 작은 값이 도출된다.

$w$ 를 1로 설정했을 경우

$w$ 의 대부분이 양쪽으로 치우치게 된다. 그럴 경우 sigmoid, tanh에서 사용할 경우 vanishing gradient problem가 생긴다.

weight의 들어오는 갯수와 나가는 갯수가 다른데 모든 상황에서 initialization 을 한다는 것이 과연 합당한가? 에 대해서 생각할 수 있고 그러한 문제에서 linear activation이라는 가정하에 Xavier initialization을 제안했다. 결국 Xavier initialization std이 $\frac{1}{\sqrt{n}}$ 이라는 가정을 했을 때 맞다는 것을 수학적으로 증명 했다.

import numpy as np
import matplotlib.pyplot as plt

D = np.random.randn(1000, 500)

hidden_layer_size = [500]* 10 # 10 : hidden layer, 500 : hidden node
nonlinearities = ['tanh'] * len(hidden_layer_size)

activate = {'relu' : lambda x : np.maximum(0, x), 'tanh' : lambda x: np.tanh(x)}
Hs = {}

for  i in range(len(hidden_layer_size)):
    X = D if i == 0 else Hs[i-1] # input at this layer
    fan_in = X.shape[1]
    fan_out = hidden_layer_size[i]

    W = np.random.randn(fan_in, fan_out) * 0.01 # layer initialization

    H = np.dot(X, W)
    H = activate[nonlinearities[i]](H)
    Hs[i] = H

Hs.items()

print ('input layer had mean %f and std %f' % (np.mean(D), np.std(D)))
layer_means = [np.mean(H) for i, H in Hs.items()]
layer_stds = [np.std(H) for i, H in Hs.items()]
for i, H in Hs.items():
    print( 'hidden layer %d had mean %f and std %f ' % ( i + 1, layer_means[i], layer_stds[i]))



plt.figure()
plt.subplot(121)
plt.plot(Hs.keys(), layer_means, 'ob-')
plt.title('layer mean')
plt.subplot(122)
plt.plot(Hs.keys(), layer_stds, 'or-')
plt.title('layer std')

plt.figure()
for i, H in Hs.items():
    plt.subplot(1, len(Hs), i+1)
    plt.hist(H.ravel(), 30, range = (-1, 1))
plt.show()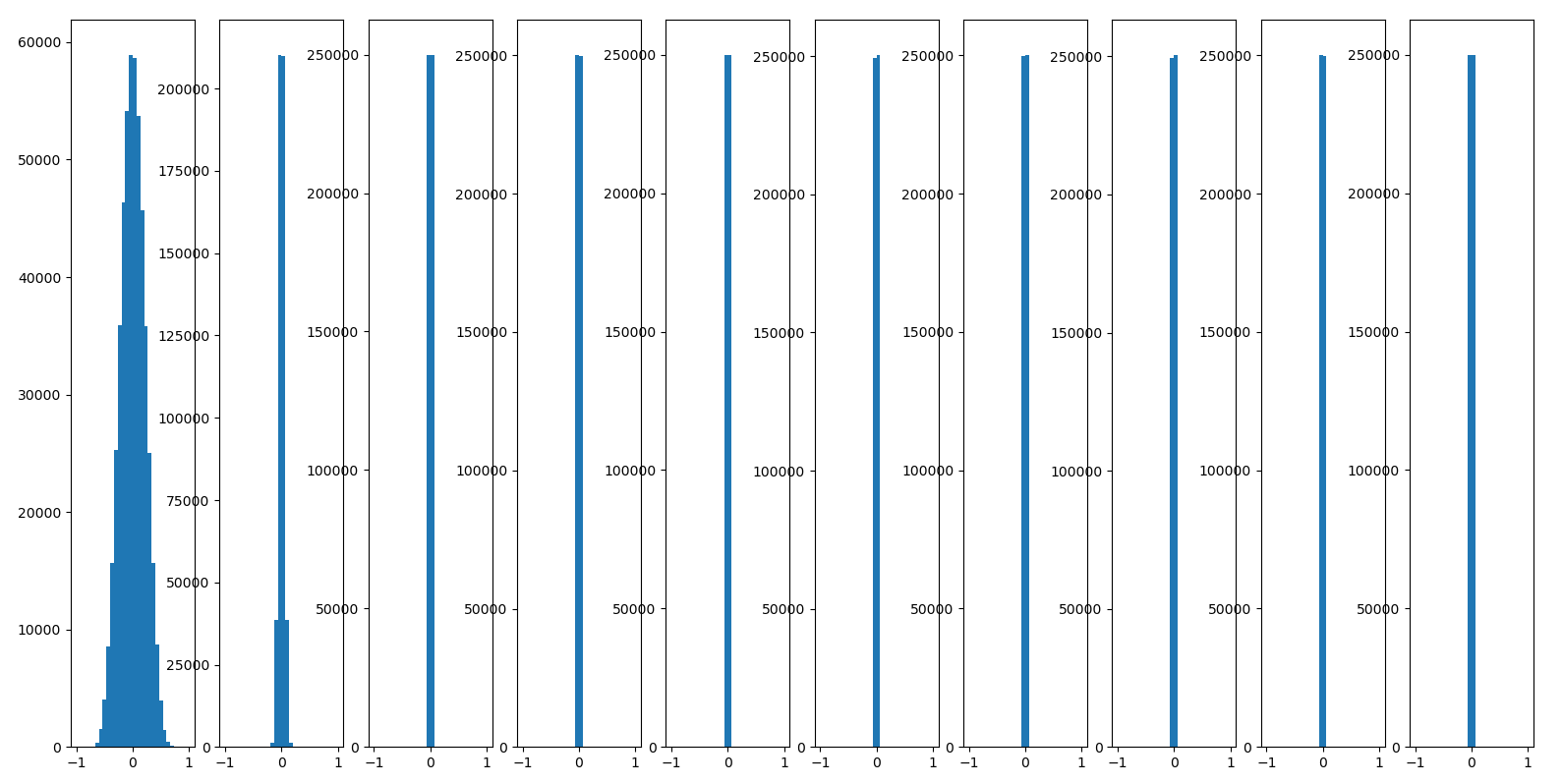

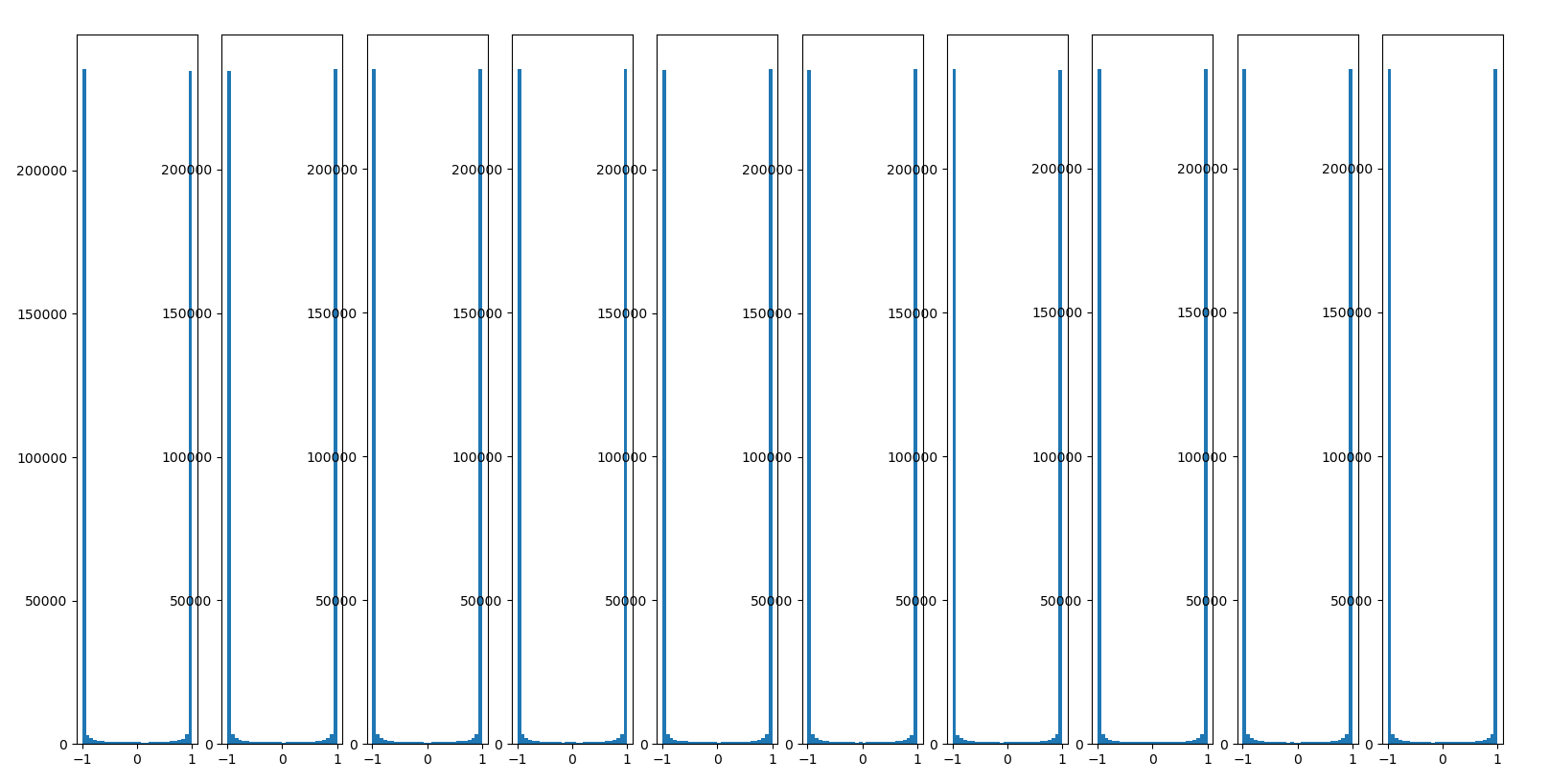
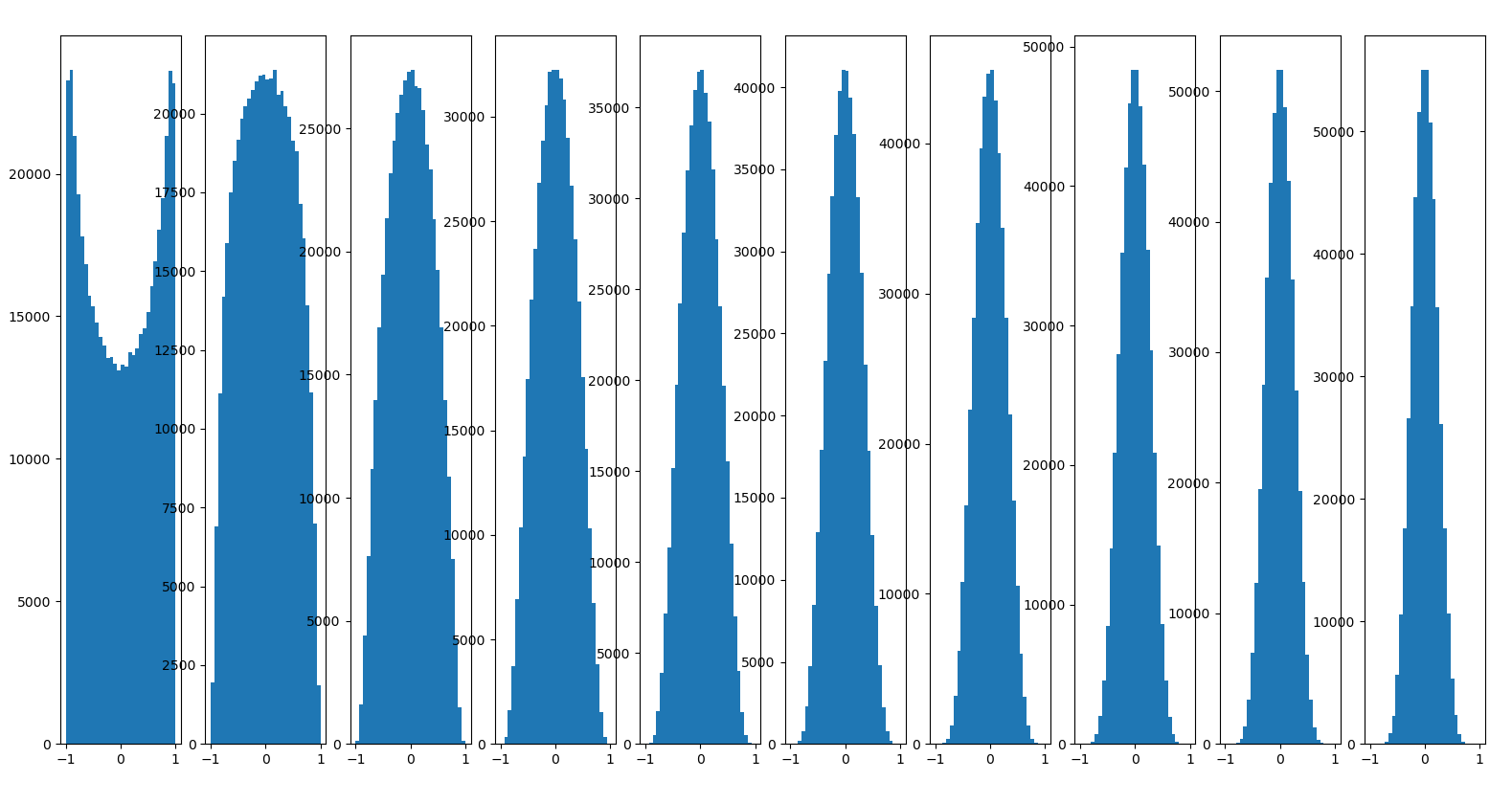
Batch Normalization

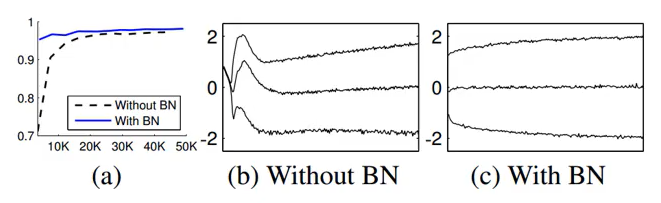
Batch Normalization은 CNN에서 거의 default로 사용하는 알고리즘이라고 할 수 있다. 상식적으로 생각을 해보았을 때 계속 Batch단위로 training을 하게 되면 분포가 변화하게 된다. 심지어 1번 layer에서 적은값으로 변하게 되어서 뒷 부분에서는 큰 값으로 변해야 된다면, Shifting 값이 점점 심해질 수 밖에 없다. 그 부분을 보정하고자 Batch Normalization이 나왔다. 아래 식에서의 $ϵ$ 은 0을 방지하기 위한 값으로 보면 된다. 결국에는 normalize를 할 수 있을 것이고 거기에 대해서 $γ (s c a l e)$ 와 $β (s h i f t)$ 값을 학습하게 된다.

BN의 장점

- 높은 learning rate도 수용할 수 있다.

- network를 통한 gradient flow가 향상된다.

- initialization 의 dependence도 줄어든다.

- regulazation 기능을 한다.

- dropout의 필요성도 줄어든다. ( dropout : hidden layer의 일부 유닛이 동작하지 않게 하여 overfitting을 막는 방법 )

Batch Normalization을 진행할 때, initialization 값으로 $γ$ 와 $β$ 를 어떻게 설정해야 하는가?

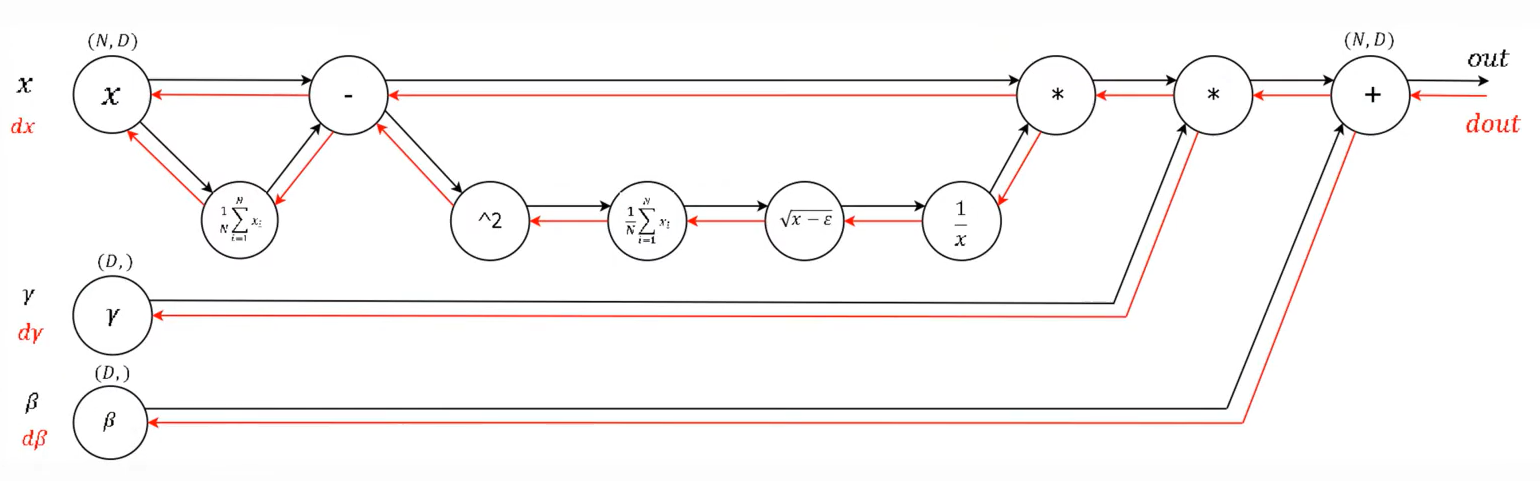
제일 처음 시작할 때는 $γ = 1, β = 0$ 을 intialization한다. 그렇게 되면 우리가 처음에 propagation을 함에 있어 어떠한 effect도 주지 않은 것이 된다. $y_{i} = \hat{x_{i}}, w h e n γ = 1, β = 0$

import numpy as np
# forward
def batchnorm_forward(x, gamma, beta, eps):
    N, D = x.shape
    # step1 : calculate mean
    mu = ( 1. / N ) * np.sum(x, axis = 0)
    # step2 : subtract mean vector of every training example
    xmu = x - mu
    # step3 : following the lower branch - calculation denominator 
    sq = xmu ** 2
    # step4 : calculate variance
    var = ( 1. / N ) * np.sum(sq, axis = 0)
    # step5 : add eps for numerical stability, then sqrt
    sqrtvar = np.sqrt(var + eps)
    # step6 : invert sqrtwar
    ivar = 1. / sqrtvar 
    # step7 : execute normalization
    xhat = xmu * ivar 
    # step8 : Nor the two transformation steps
    gammax = gamma * xhat
    # step9 
    out = gammax + beta
    cache = (xhat, gamma, xmu, ivar, sqrtvar, var, eps)
    return out, cache



# backward
def batchnorm_backward(dout, cache): # local gradient 
    # unfold the variable stored in cache
    xhat, gamma, xmu, ivar, sqrtvar, var, eps = cache
    # get the dimentions of the input / output
    N, D = dout.shape 
    # step 9 
    dbeta = np.sum(dout, axis = 0)
    dgammax = dout
    # step 8
    dgamma = np.sum(dgammax * xhat, axis = 0 )
    dxhat = dgammax * gamma 
    # step 7
    divar = np.sum(dxhat * xhat, axis = 0 )
    dxmu1 = dxhat * ivar
    # step 6
    dsqrtvar = -1. / (sqrtvar ** 2) * divar
    # step 5
    dvar = 0.5 * 1. / np.sqrt(var + eps) * dsqrtvar 
    # step 4
    dsq = 1. / N * np.ones( (N, D) ) * dvar
    # step 3
    dxmu2 = 2 * xmu * dsq 
    # step 2 
    dx1 = (dxmu1 + dxmu2) 
    dmu = -1 * np.sum(dxmu1 + dxmu2, axis = 0 )
    # step 1
    dx2 = 1. / N * np.one( (N, D) ) * dmu
    # step 0 
    dx = dx1 + dx2 
    return dx, dgamma, dbeta

저작자표시

'Deep Learning > CS231N' 카테고리의 다른 글

[CS231N] Convolution Neural Networks(CNN) (2)	2021.07.14
[CS231N] Optimization의 종류 - SGD부터 Adam까지 (0)	2021.07.12
[CS231N] Neural Network Back-propagation (0)	2021.07.06
[CS231N] Loss function & Optimization (2) (0)	2021.07.05
[CS231N] Loss function & Optimization (1) (0)	2021.07.05

현재글[CS231N] 활성화 함수(Activation Fucntion)의 종류

ok-lab Machine Learning, Deep Learning을 전반적으로 다룹니다.

내 블로그 - 관리자 홈 전환	`Q` `Q`
새 글 쓰기	`W` `W`

글 수정 (권한 있는 경우)	`E` `E`
댓글 영역으로 이동	`C` `C`

이 페이지의 URL 복사	`S` `S`
맨 위로 이동	`T` `T`
티스토리 홈 이동	`H` `H`
단축키 안내	`Shift` + `/` `⇧` + `/`

ok-lab