[CS224N] Language Model (n-gram, NNLM, RNN)

Contents

• Language Model 이란?
  • n-gram Language Models
  • Window-based Neural Network Language Model(NNLM)

 

 

Language Model 이란?

단어의 시퀀스에 대해서 얼마나 자연스러운 문장인지를 확률을 통해 예측하는 모델이며, 주어진 단어의 시퀀스에 대해 다음에 나타날 단어가 어떤 것인지를 예측하는 작업을 Language Modeling이라고 한다. 기계번역, 음성인식, 자동완성 등 여러 분야에 사용될 수 있다. 

 

$w_1,w_2,\cdots ,w_{t-n+1},\cdots ,w_{t-1},w_t,\cdots ,w_{T-1},w_T$

 

$P(w_1,\cdots ,w_T)=P(w_1)\times P(w_2|w_1)\times \cdots \times P(w_T|w_{T-1},\cdots ,w_1)$

 

$\underset{t=1}{\prod ^T}P(w_t|w_{t-1},\cdots ,w_1)$

 

 

 

n-gram Language Models

Neural Network 이전에 사용되었던 Language Model이며, 예측에 사용할 앞 단어의 개수를 정하여 모델링하는 방법이다. n-gram은 n개의 연이은 단어의 뭉치라고 불린다. n-gram model은 window size 만큼 단어를 고려하여 계산한다.

 

e.g. ) the students opened their

uni-gram : 'the', 'students', 'opened', 'their'

bi-gram : 'the students', 'students opened', 'opened their'

tri-gram : 'the students opened', 'students opened their'

4-gram : 'the students opened their'

 

 

$w_1,w_2,\cdots ,w_{t-n+1},\cdots ,w_{t-1},w_t,\cdots ,w_{T-1},w_T$

 

$P(w_1,\cdots ,w_T)=P(w_1)\times P(w_2|w_1)\times \cdots \times P(w_T|w_{T-1},\cdots ,w_1)$

 

$\underset{t=1}{\prod ^T}P(w_t|w_{t-1},\cdots ,w_{t-n+1})$

 

 

4-gram이라고 하면 4-1개의 단어를 고려해 그 단어가 전체 문장에 출현한 빈도와 다음 단어 $w$가 포함되어 출현한 빈도의 확률값을 가져와 가장 높은 확률값을 가지는 단어를 추천해주는 방법이다. 

 

$P(w|studentsopenedtheir)=\frac{count(studentsopenedtheirw)}{count(studentsopenedtheir)}$

 

 

 

n-gram 기반 Language Models 문제점

1. Sparsity problems : n이 커질수록 안좋아지며, 일반적으로 n<5로 설정

위 경우를 예로 들면 'students opened their'이 데이터에서 한번도 등장하지 않는 경우 확률 계산이 불가한 경우 'opened their' 형태로 n-1 개 단어가 아닌 n-2, n-3 등의 형태로 n-gram의 형태를 낮추어주는 방향으로 해결이 가능하다. (backoff) 분자의 경우 'students opened their $w$'가 나타나지 않는 경우 $w\in V$의 count에 작은 값의 $\delta$를 더해주면서 smoothing 하게 해준다. 

 

2. Storage problems : n이 커지거나 corpus가 증가하면 모델의 크기가 증가

n이 커지는 경우 Corpus 내 모든 n-gram에 대한 count를 저장해 주어야 하는데 이 경우 모델의 크기가 너무 커지는 문제가 발생한다. 

 

위 문제를 해결하기 위해 Neural Network 기반의 모델이 등장했다. 

 

 

Window-based Neural Network Language Model(NNLM)

'curse of dimensionality'를 해결하기 위해 제안된 신경망 기반 Language Model이다. Language Model이면서 동시에 단어의 'distributed representation'을 학습한다. window size 만큼의 단어들을 one-hot vectors로 만들고 vector를 concate해 word embeddings을 한 후 hidden layer를 거쳐 최종적으로는 sotfmax로 분류를 하게 된다. 단어의 embedding을 통해 sparsity problem을 해결하고, 관측된 n-gram을 저장할 필요가 없어졌다. 하지만 고정된 window size가 너무 작다는 것이고, window size를 키우면 학습시킬 w또한 커지기 때문에 계산 속도가 너무 오래걸리는 단점이 있다.  

 

 

 

 

Recurrent Neural Network(RNN)

재귀 모델이라고도 하며, input이 들어가면 hidden states에서 학습을 하고 출력된 값의 일부가 다시 되돌아가 값을 조정하는 모델이라고 할 수 있다. RNN 모델의 특징은 동일한 가중치 W를 반복적으로 적용하기 때문에 기존의 신경망 모델의 단점을 해결할 수 있다. 

 

장점

- 입력의 길이에 제한이 없다.

- 이론적으로 길이가 긴 timestep t에 대해 처리 가능하다.

- 입력에 따른 모델의 크기가 증가하지 않다

- 매 timestep t 에 동일한 가중치를 적용하므로 symmetry 하다.

 

단점

- 단어가 입력에 하나씩 주어지기 때문에 Recurrent 계산이 느리다.

- 실제로는 길이가 긴 timestep t 에 대해 처리가 안된다. 

 

 

Training a RNN Language Model

1. $x_1,\cdots ,x_T$의 단어들로 이루어진 시퀀스 Corpus를 준비한다.

2. $x_1,\cdots ,x_T$를 차례대로 RNN-LM에 주입하고, 매 step t 에 대한 $\widehat{y_t}$를 계산한다.

   - 주어진 단어에서부터 시작하여 그 다음 모든 단어들에 대한 확률을 예측

3. Step t에 대한 손실함수 Cross-Entropy를 계산한다. ( $y_t$ is one-hot for $x_{t+1}$)

 

$L_t=CE(y_t,\widehat{y_t})=-\underset{w\in |V|}{\mathrm{\Sigma }}{y}_{t,w}\times log(\widehat{y_{t,w}})=-log(\widehat{y_{t,x_{t+1}}})$

 

4. 전체 step T에 대해 계산한 손실함수 $L_t$의 평균을 계산한다.

 

$L=\frac{1}{T}\underset{t=1}{\stackrel{T}{\mathrm{\Sigma }}}{L}_t=-\frac{1}{T}\underset{t=1}{\stackrel{T}{\mathrm{\Sigma }}}\underset{w=1}{\stackrel{|V|}{\mathrm{\Sigma }}}{y}_{t,w}\times log(\widehat{y_{t,w}})=-\frac{1}{T}\underset{t=1}{\stackrel{T}{\mathrm{\Sigma }}}-log(\widehat{y_{t,x_{t+1}}})$

 

 

 

모델을 만들고 난 후 모델을 평가하는 방법은 다음과 같다.

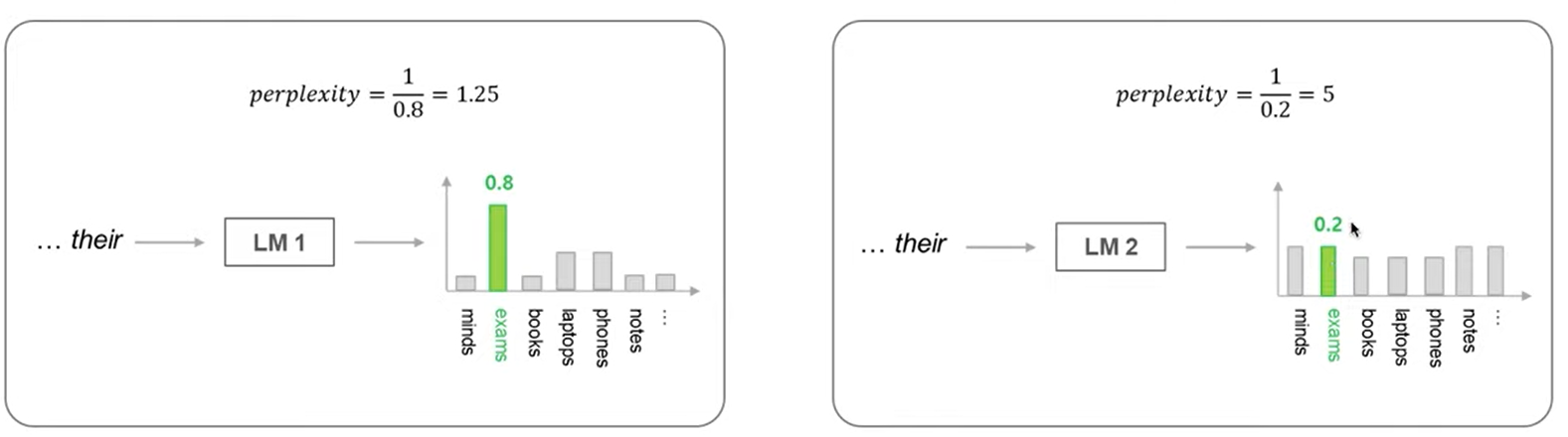
- Language Model은 주어딘 과거 단어로 부터 다음에 출현할 확률분포를 출력하는 모델

- Language Model을 평가하는 대표적인 척도인 Perplecity를 사용

- Perplexity는 출현할 단어의 확률에 대한 역수${}^{inverse}$라고 할 수 있음

- Perplexity의 값이 작을수록 좋은 Language Model

 

$perplexity=\underset{t=1}{\prod ^T}{\left(\frac{1}{P_{LM}(x_{t+1}|x_t,\cdots x_1)}\right)}^{1/T}$

 

= $\underset{t=1}{\prod ^T}{\left(\frac{1}{\widehat{y_{t,x_{t+1}}}}\right)}^{1/T}=exp(\frac{1}{T}\underset{t=1}{\stackrel{T}{\mathrm{\Sigma }}}-log(\widehat{y_{t,x_{t+1}}}))=e^L$

 

왼쪽모델이 오른쪽 모델보다 더 좋은 모델이다.