[Statistics] T test with R

 

T test 는 주로 평균검정을 할 때 사용한다. 평균검정이란 평균에 대한 가설검정을 의미하며 선정한 표본이 특정 평균값을 갖는 모집단에 속하는지 또는 두 표본집단의 평균값 간에 차이가 존재하는지에 대해 검정하는 것이다. 평균검정의 종류로는 일표본, 독립표본, 대응표본 등이 있다. t test의 가설은 다음과 같다.

 

$ H_{null}\ :\ \mu\ =\ a $

$ H_{a}\ :\ \mu\ \neq \ a $

 

연구자가 찾고자하는 결과는 기존과 다르다라는 주장이며 대립가설로 설정한다. t test에서는 $\sigma$를 사용하지 않고, 표본의 표준오차인 $s \over \sqrt{n}$ 를 사용한다. 다음과 같이 정의되는 t값을 검정통계량(test statistic)으로 사용하여 검정한다. 

 

$ t = {\bar{X} - \mu \over {s \over \sqrt{n}}} $

여기에서, t는 t-value, $\bar{X}$는 표본평균, $\mu$는 모집단의 평균, s는 standard error

 

 

예를들어 경영자 20명의 혈압을 측정한 결과 평균 135mmHg, 표준편차 25mmHg라고 하자. 30대 및 40대 연령층의 혈압이 평균 115mmHg라고 할 때 경영자의 혈압이 일반 사람들과 다르다는 주장을 검정해보자.

 

$ t = {135 - 115 \over {25 \over \sqrt{20} } } = 3.58 $

 

3.58로 t-value가 2$\sigma$를 넘어가기 때문에 귀무가설을 기각하고, 대립가설을 채택하므로 경영자들의 혈압은 일반인들의 혈압과 차이가 있다라는 것을 확인할 수 있다. 

pt(3.58, df=19, lower.tail=FALSE)*2

# 0.001997274

pt function을 사용해서 t-value를 입력하면 p-value값을 도출할 수 있다. p-value <0.05이기 때문에 귀무가설을 기각하는 결론이 도출된다. 뒤에 *2를 한 이유는 one-side test일 경우 대립가설이 일반 사람들보다 혈압이 크다라는 것이기 때문에 *2를 해주는 것이다. ( 같지 않다라는 가설을 세우게 되면 *2를 하지 않아도 된다. )

 

t 분포를 가지고 신뢰구간을 구하는 방법은 다음과 같다.

$ \mu - t_{0.05,19}(=2.09) \times {s \over \sqrt{n}} \le \bar{X} \le \mu + t_{0.05,19}(=2.09) \times {s \over \sqrt{n}} $

 

이처럼 t 분포의 가설검정을 하는 방법은 여러가지가 존재한다. 위 경우 신뢰구간을 95%로 설정해서 검정통계량이 2.09가 되었지만 만약 신뢰구간을 99%로 설정하고 싶다면 $t_{0.01,19}$ 를 사용해 2.86을 사용하면 된다.

qt(0.005, df = 19, lower.tail = FALSE)

# 2.860935

 

위 예제의 신뢰구간을 구하면 다음과 같다.

$ \mu - t_{0.05,19}(=2.09) \times {s \over \sqrt{n}} \le \bar{X} \le \mu + t_{0.05,19}(=2.09) \times {s \over \sqrt{n}} $

 

$ \bar{X} - t_{0.05,19}(=2.09) \times {s \over \sqrt{n}} \le \mu \le \bar{X} + t_{0.05,19}(=2.09) \times {s \over \sqrt{n}} $

 

$135 - 2.09 \times {25 \over \sqrt{20}} \le \mu \le 135 + 2.09 \times {25 \over \sqrt{20}} $

 

$ 123.3 \le mu \le 146.7 $

 

이항을 하면서 전개를 하게 되는데, 만약 t-test를 처음 접해본다면 위 식을 직접 전개해보는 것을 추천한다. 단순히 훑고 넘어가는 것과 직접 손으로 전개해보는 것은 큰 차이가 있다.

 

 

one-sample t test

일표본 평균검정은 하나의 표본 데이터를 이용하여 모집단의 평균이 특정 값과 같은지 검정한다. 검정에 쓰일 예제는 MASS 패키지에 포함되어 있는 cats 데이터셋을 이용할 것이다. (R을 이용하여 분석한다) 고양이의 몸무게의 평균이 2.6인가에 대해 test를 해보았을 때 p-value = 0.002673로 거의 0에 가까우며 평균이 2.6kg이라는 귀무가설을 기각하게 된다. 

 

 

몸무게의 평균이 2.7kg라고 가설을 조정하니 p-value가 0.05보다 커지며 귀무가설을 채택, 대립가설을 기각하게되고 고양이의 평균 몸무게는 2.7kg라는 귀무가설을 만족하게 된다. 

위 t-test를 좀 더 보기 쉽도록 시각화해주었다.

 

 

만약 two-side를 하지 않고 크거나 작다라는 가설을 세우고 싶다면 alternative method를 'greater' 또는 'less' 등으로 수정을하면 원하는 결과를 도출할 수 있을 것이다. 추가 상세한 정보를 얻고 싶으면 str(t.test)를 통해 인자를 추출할 수 있다.

 

 

지금까지는 계속 평균이 같은지 다른지에 대해서 평가했다. 지금부터는 표본 데이터를 이용해 모집단의 비율에 대한 통계적 검정을 수행하는 절차를 확인해보자. 김모씨는 스포츠 회사에 다니면서 본인이 좋아하는 야구팀이 초반에 30경기 가운데 18승을 거두었다며 팀의 승률이 50%가 넘는다고 주장하고 있을 때 해당 주장이 통계적으로 타당한지 검정할 수 있을 것이다. 

 

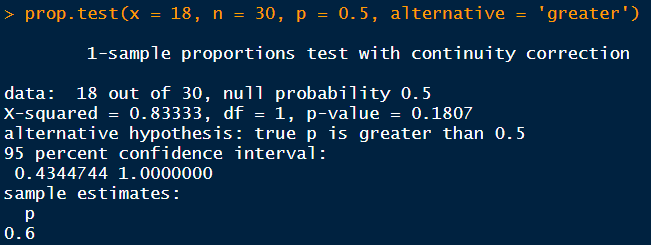
prop.test를 시행한 결과를 보면 p-value가 0.18로 유의확률보다 크기 때문에, 승률이 50%보다 크다고 주장할만한 충분한 증거가 되지 못한다. 

 

 

 

two - independent samples t test

독립표본 평균검정은 두 개의 독립표본 데이터를 이용하여 각각 대응되는 두 개의 모집단 평균이 서로 동일한지 검정한다. 예를 들면 남녀 간의 영어시험 점수에 차이가 있는지, 흡연자 비흡연자 간의 폐질환 발생률이 차이가 있는지 등이 잇다. R에서 분석을 할 때에는 함수의 첫 번째에 formula형식으로 인수를 지정한다. 

 

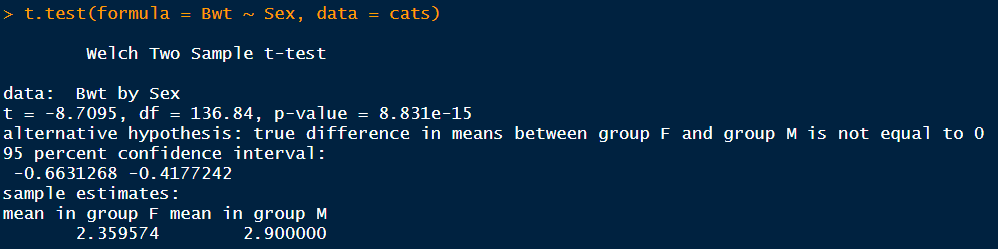
p-value가 매우 작은 것을 확인할 수 있다. 따라서 암컷 고양이와 수컷 고양이 두 집단의 몸무게 차이가 없다는 귀무가설을 기각하고, 몸무게가 차이난다는 대립가설을 채택할 수 있다. confidenc interval을 보면 -0.66 ~ 0.41 로 몸무게 차이가 존재하는 것을 확인할 수 있다.

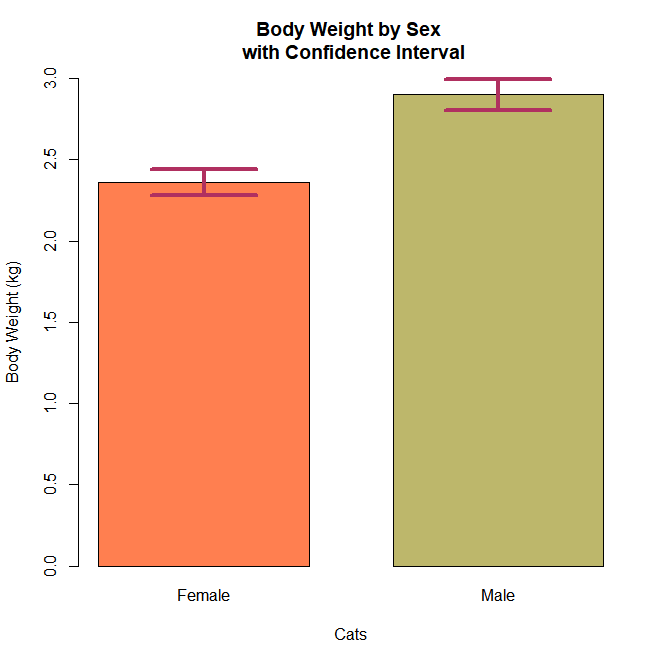
bars <- tapply(cats$Bwt, cats$Sex, mean)
lower <- tapply(cats$Bwt, cats$Sex, function(x) t.test(x)$conf.int[1])
upper <- tapply(cats$Bwt, cats$Sex, function(x) t.test(x)$conf.int[2])

if (!require('gplots')) install.packages('gplots')

library(gplots)


barplot2(bars, space=0.4, ylim=c(0, 3.0),
         plot.ci=TRUE, ci.l=lower, ci.u=upper, ci.color='maroon', ci.lwd=4,
         names.arg=c('Female', 'Male'), col=c('coral', 'darkkhaki'),
         xlab='Cats', ylab='Body Weight (kg)',
         main='Body Weight by Sex \n with Confidence Interval')