Semi-Supervised Classification With Graph Convolutional Networks (ICLR'17)

 

Contents

 

Contribution

본 논문은 Graph Convolution Network (GCN)을 처음 제안한 논문이며, GCN은 Adjacency Matrix, Degree Matrix 혹은 Feature Matrix를 이용하여 그래프를 Representation하는 신경망이다. GCN에는 Spatial GCN과 Spectral GCN이 존재하는데, 본 논문에서는 Spectral GCN을 통해 두 가지 Contribution을 했다고 언급한다. 

 

1. 간단하고 잘 작동(behave)하는 Layer-wise Propagation rule을 설명하고, 이 방법이 Spectal graph Convolution의 빠르고 효율적인 1차 근사임을 증명한다. 

 

2. 기존의 semi-supervised 연구들에서는 $\mathcal{L} = \mathcal{L}_0 + \lambda \mathcal{L}_{\text{reg}} $과 같은 형태로 모델을 학습하였으나, 이는 연결된 노드들이 유사하다는 가정(동일한 Label을 가질 확률이 높음)을 갖고 있기 때문에, 유사도 이외의 추가적인 정보를 담지 못하게 되어 모델의 능력을 제한한다.

 

 

Introduction

본 논문에서 제안하는 GCN(Graph Convolution Network)에서는 Adjacency Matrix를 입력으로 사용하여 어떤 노드들이 연결되어 있는지에 대한 정보를 직접 이용하여, 제한된 능력을 극복할 수 있다. 

\[ \mathcal{L}_{\text{reg}} = \sum_{i, j} = A_{ij} || f(X_i) - f(X_j)||^2 = f(X)^{\text{T}} \Delta f(X) \]

$\mathcal{L}_0$는 그래프에서 라벨링된 부분에 대한 loss를 의미한다. $X$는 feature vector를 의미하고, $\Delta = D - A$는 undirected graph $\mathcal{G} = (\mathcal{V}, \mathcal{E}) $의 정규화를 진행하지 않은 Laplacian을 의미한다. 위 수식은 그래프의 연결된 노드가 동일한 Label을 공유할 가능성이 있다는 가정에 의존하여 학습을 진행하기 때문에, 모델의 능력(capacity)을 제한한다고 언급하며 GCN을 제안한 것이다. 

 

Semi-Supervised Node Classification

 

Fast Approximate Convolution on Graphs

본 논문에서는 Graph-based Neural Network model $f(X,A)$를 다음과 같이 정의하였다. 

\[ H^{l+1} = \sigma ( \tilde{D}^{\frac{1}{2}} \tilde{A} \tilde{D}^{\frac{1}{2}} H^{(l)} W^{(l)}) \]

$\tilde{A} = A + I_N$을 의미하며, 무향 그래프(undirected graph) $\mathcal{G}$의 인접 행렬에 self-connection을 더한 것이다. $H^{(l)} \in \mathbb{R}^{N \times D}$는 $l^{\text{th}}$ layer의 propagation 결과를 의미한다. 즉, Node의 값을 의미한다. 위 수식을 Deep Learnig 스타일로 변환하면 아래와 같다. 

\[ Z = f(X, A) = \text{softmax}(\hat{A} \cdot \text{ReLU} (\hat{A} X W^{(0)} ) W^{(1)} ) \]

해당 논문은 이처럼 Spectral Convolution Network를 1차 근사만으로도 계산할 수 있게 만들어 Deep Learning 관점에서 접근성이 좋게 만들어주었기 때문에 매우 우수한 논문으로 인정받는 것 같다. 

 

Spectral Graph Convolution

해당 논문에서 이론은 2 페이지 내로 정리가 완료 되었으나, 이를 이해하기 위해서는 다양한 개념을 이해하고 있어야 하기에 하나하나 풀어서 설명하고 나갈 것이다. Graph에서의 Spectral Convolution은 Fourier Transform을 통해 eigen-decomposition을 수행하는 것이며, 수식은 다음과 같다. 

\[ g_{\theta} \star x = U g_{\theta}^* U^T x \]

Fourier Transform에 대한 상세한 내용은 여기를 참고하길 바란다. Fourier Transform은 주파수마다 Signal을 출력하는데, 이 때 주파수에는 Singal을 사영(Projection)하는 Fourier Bases가 존재한다. 그렇기 때문에 고유 분해 즉, eigen-decomposition을 수행하여 이를 찾는 것이다. 

 

Graph의 관점에서 바라보게 되는 경우 Graph signal을 Frequency별로 분해하는 과정으로 볼 수 있다. 이때 Graph signal은 Node의 Feature를 의미하고, Frequency는 Node 간의 차이를 의미한다. 만약 Node 간의 차이가 적다면 Frequency는 낮을 것이다.

 

Graph에서 Laplacian Matrix는 $L = D-A$로 연산된다. 수식적으로 접근하는 경우 Degree Matrix와 Adjacency Matrix 간의 차이로 볼 수 있으나, Adjacency Matrix는 Diagonal이 없기 때문에 두 행렬의 합으로 이해하면 된다. 

위 그림을 통해 우리는 difference operator와 Laplacian quadrativ form을 정의할 수 있다. 

\[ \begin{equation} \begin{split} \text{difference operator} & : Lf = \sum^N_{i,j=1} A_{ij} (f(i) - f(j)) \\ \text{Laplacian quadratic form} & : f^TLf = \frac{1}{2} \sum^N_{i,j=1} A_{ij} (f(i) - f(j))^2 \end{split} \end{equation} \]

Laplacian quadratic form은 signal이 얼마나 smooth한지를 확인할 수 있다. 예를 들어, 인접한 노드들 간의 Signal이 큰 차이가 없는 경우 $f^TLf$ 값은 낮은 값을 보이며, 인접한 노드들 간의 Signal의 차이가 큰 경우 $f^TLf$는 큰 값을 가진다.

 

그러나 이와 같이 Eigen Decomposition을 하는 방식은 모든 Eigen value를 다 사용하기 때문에 Localized가 되지 않고, 또한, 계산 비용이 너무 크다. 이러한 문제를 해결하기 위해 본 논문에서는 Chebyshev polynomial을 사용하여 다항식 자체를 근사하는 형태로 진행하며, 수식은 다음과 구성하였다.

\[ \begin{equation} \begin{split} g_{\theta'} \star x & \approx \theta'_0 T_0(\tilde{L})x + \theta'_1T_1(\tilde{L})x +\ \cdots\ +\theta'_k T_k (\tilde{L})x \\  & = \sum^K_{k=0} \theta'_k T_k (\tilde{L})x \end{split} \end{equation} \]

Chebyshev polynomial은 재귀형태로 계산되며, $T_0(x)=1, \ T_1(x) = x$를 초기값으로 설정한다.

 

Layer-wise Linear Model

본 논문에서는 Chebyshev polynomial을 사용하지만 K=1 까지만 사용한다. K=1로 지정하는 경우 Chebyshev polynomial은 다음과 같이 Graph에 대해 선형 함수가 된다. 

\[ \begin{equation} \begin{split} g_{\theta'} \star x & \approx \sum^1_{k=0} \theta'_k T_k(\tilde{L})x \\ \\ & \approx \theta'_0x + \theta'_1 T_1(\tilde{L})x \\ \\ & \approx \theta'_0x + \theta'_1 T_1(\frac{2}{\lambda_{\text{max}}}L - I_N) x \\ \\ & \approx \theta'_0x + \theta'_1 T_1(I_N - D^{-\frac{1}{2}} A D^{-\frac{1}{2}} - I_N) x \\ \\ & \approx \theta'_0 x - \theta'_1 D^{-\frac{1}{2}} A D^{-\frac{1}{2}} x \\ \\ & \approx \theta(I_N + D^{-\frac{1}{2}} A D^{-\frac{1}{2}})x \end{split} \end{equation} \]

본 논문에서 GCN의 linear formulation에서는 $\lambda_{text{max}} \approx 2$임을 확인하였으며 $\theta = \theta'_0 = -\theta'_1$로 설정하였다. 또한, 논문에서는 normalized Laplacian Matrix를 사용하고 있으며, normalized Laplacian Matrix의 수식은 다음과 같다. 

\[ \begin{equation} \begin{split} L^{\text{norm}} & = D^{-\frac{1}{2}} L D^{-\frac{1}{2}} \\ & = I_N - D^{-\frac{1}{2}}A D^{-\frac{1}{2}} \end{split} \end{equation} \]

최종적으로, $\theta (I_N + D^{-\frac{1}{2}} A D^{-\frac{1}{2}}$를 renoramlization 함으로써 다음과 같은 수식을 구할 수 있다. 

\[ \begin{equation} \begin{split} \text{renormalization trick} & : I_N + D^{-\frac{1}{2}} A D^{-\frac{1}{2}} \rightarrow \tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}}, \\ \\ \text{ with } \tilde{A} & = A + I_N \text{ and } \tilde{D}_{ii} = \sum_j \tilde{A}_{ij} \\ \\ Z & = \tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}} X \Theta \end{split} \end{equation} \]

$\Theta \in \mathbb{R}^{C \times F}$는 filter parameter matrix를 의미하고, $Z = \mathbb{R}^{N \times F}$는 convolved signal matrix를 의미한다. 

 

Semi-supervised node Classification

이처럼 많은 trick을 가한 후 최종적으로 $Z$를 Deep Learning form으로 변환하면 다음과 같다.

\[ \begin{equation} \begin{split} Z & = \tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}} X \Theta \\ Z & = f(X, A) = \text{softmax}(\hat{A} \cdot \text{ReLU} ( \hat{A} X W^{(0)} ) W^{(1)} ) \end{split} \end{equation} \]

위 수식을 통해 two-layer GCN을 구성할 수 있다. $W^{(0)} \in \mathbb{R}^{C \times H}$는 input과 hidden을 연결하는 weight matrix를 의미하고, $W^{(1)} \in \mathbb{R}^{H \times F}$는 hidden 과 output을 연결하는 weight matrix를 의미한다. learnable parameter가 주어졌으니 학습은 어떻게 진행되는지 알아보자. 

\[ \mathcal{L} = - \sum_{l \in \mathcal{Y}_L} \sum^F_{f=1} Y_{lf} \text{ln}Z_{lf} \]

$\mathcal{Y}_L$은 라벨링된 노드들의 집합을 의미한다. 위 수식을 살펴보면, 실제 학습하는 경우에는 라벨링되지 않은 데이터는 사용하지 않고, 라벨링된 노드들만 사용하는 것을 확인하할 수 있다. 

 

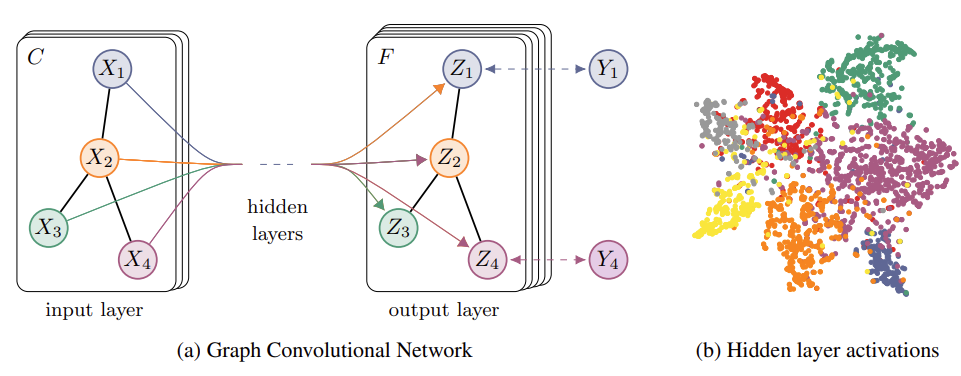
Experiments

본 논문에서 제안하는 GCN의 성능을 검증하기 위해 해당 논문의 세팅을 그대로 따라 진행하였다. 

Node는 논문을 사용하였고, Egde는 논문들 간의 인용을 의미한다. Label rate는 각 데이터셋에서 훈련에 사용되는 node를 전체 노드 개수로 나눈 비율을 의미하며, Node Feature와 Label은 각각 Bag of Words, Node Label을 의미한다. 

 

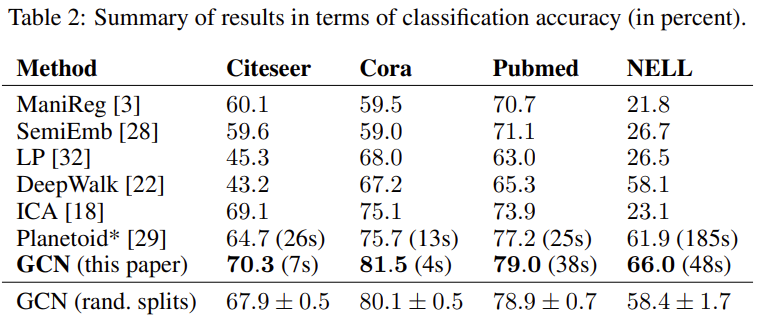
당연하게도, 기존 논문에서 제안한 모델들 보다 본 논문에서 제안하는 GCN의 성능이 우수한 것을 확인하였다. 

 

 

위 그림은 Chebyshev filter를 2차, 3차 다항식으로 계산한 값과, 1$^{\text{st}}$-order model을 한 경우와 single parameter, Renormalization trick을 사용한 경우와 비교한 결과 Renormalization trick을 사용한 경우 가장 우수한 성능을 보이고 있다. 

 

 

Future Work 

본 논문에서는 총 3가지의 추가 연구를 제안하고 있다. 

 

Memory Requirement

현재 실험에서는 모든 Neighbor를 담아야 하기 때문에 Full Batch Gradient Descent 방식을 사용하였다. 이는 많은 메모리가 요구되기 때문에 추후에는 Minibatch로 전환하기 위한 실험이 필요하다.

 

Directed edges and edge features

현재 GCN은 Undirected Graph에 한정적으로 사용이 가능하다(weighted or unweighted). 

 

Limiting assumptions

현재 GCN은 Self-connection과 Neighborhood Edge 간에 같은 중요도를 설정해두고 계산을 진행하였다. 그러나 둘에 대한 중요도를 조절할 수 있는 파라미터를 추가하는 경우 보다 우수한 성능이 도출될 수 있다. 

\[ \tilde{A} = A + I_N \Rightarrow \tilde{A} = A + \lambda I_N \]