Contents
Attention이라는 개념은 자연어처리(Natural Language Processing; NLP)를 공부하는 사람이라면 한 번쯤은 들어봤을 개념이다. RNN에서 장기 의존성 문제로 인해 LSTM, GRU 등의 모델이 제안 되었으나, 이 역시도 장기 의존성 문제를 완벽히 해결할 수 있진 않았다. 이를 해결하기 위해 나온 개념이 Attention 개념이다. Attention의 기본 아이디어는 입력 받은 데이터를 매 step 마다 참고하여 중요한 혹은 관련이 있다고 판단되는 정보에 치중되어 결과값을 산출하는 방식이다. 본 논문은 이러한 매커니즘을 그래프에 적용한 Graph Attention Networks (GAT)를 제안하였다.
Introductions
이미지나 기계 번역, 감성 분석 등의 다양한 태스크에 성능이 우수하다고 알려진 CNN을 적용하는 연구가 많이 진행되고 있었다. 그로 인해 그래프에서도 CNN을 적용할 수 없을까하는 생각으로 GCN이 제안되었으며, 본 논문도 우수하다고 알려진 Attention 메커니즘을 그래프에 적용시키고자 하였다.
Attention은 주로 기계 번역과 같이 시퀀스(Sequential)한 구조를 가지고 있는 태스크에서 많이 사용되었다. Attention은 다양한 사이즈의 입력을 다룰 수 있고, 출력값을 반환할 때 입력값에 동일한 가중치를 부여하는 것이 아니라 관련성이 높은 부분에 집중하여 값을 반환한다. 만약 단일 시퀀스에 대해서 계산하는 경우 이를 Self-attention 혹은 Intra-attention이라 부르며, 이는 RNN이나 Convolution base 모델의 성능을 개선할 뿐만 아니라 기계 번역 태스크에서는 Sota(State-of-teh-art) 성능에 도달할 정도로 파워풀한 메커니즘이다.
본 논문은 Attention의 영향을 받아 그래프 구조의 node classification을 attention base 구조로 표현한 GAT를 제안한다. GAT는 Self-attention 전략(Strategy)을 따르면서 진행되며 다음과 같은 성질(Property)을 가진다. 첫 번째, 연산이 효율적이다. node의 이웃 쌍에 대해서 병렬 처리가 가능하기 때문에 기존의 그래프 관련 연구에 비해 매우 효율적이다. 두 번째, 가중치를 부여하는 것이 가능하다. 세 번째, 'inductive' learning problem에 바로 적용이 가능하다. 기본적으로 그래프에서는 서로 다른 구조를 가지는 경우 성능이 제대로 발현되지 않을 수 있으나 Self-attention을 사용하는 GAT에서는 가능하다.
본 논문에서는 기존의 Spectral based, non spectral based의 문제점을 지적하면서 본 논문의 contribution을 기술한다. Spectral based 방식은 기본적으로 푸리에 변환을 기저로 두고 있다. 초창기에는 multi-level Clustering에서 시작해, Chebyshev Polinomial을 사용하는 ChevNet, 그 후 널리 알고 있는 GCN이 제안되었다. GCN의 경우도 ChevNet의 first-order 만을 사용해 renormalization trick으로 성능을 개선하였다. 이것마저도 eigendecomposition을 사용해야 하기 때문에 전체 그래프의 구조를 알고 있어야 한다. 그러나 GAT에서는 전체 구조를 알고 있지 않더라도 학습을 할 수 있다는 것이 핵심이다.
non spectral based는 Spatial based Convolution Networks를 의미한다. Spatial based는 기본적으로 기존의 CNN을 참고하여 고정된 길이의 이웃에 대해서만 고려하여 이웃 노드를 가져와 사용하는 방식이다. 반면에 GAT는 이웃 전체에 대해서 학습하기 때문에 보다 효율적으로 inductive learning을 할 수 있다.
GAT Architecture
이번 장에서는 GAT를 구성하는 Block Layer을 제시하고 이전 연구에서 제안된 GNN의 기법들과 비교함으로써 GAT의 이론적, 실용적 이점 및 한계를 다룬다.
Graph Attentional Layer
본 논문에서 제안하는 Graph Attentional Layer 중 Single Graph Attentional Layer에 대해서 먼저 알아보자. single은 말 그대로 graph attention layer를 하나만 쌓은 구조를 의미한다. 먼저, 입력으로 node feature의 집합인
이를 학습하기 위해 모든 node에 대해서 weight matrix
위에서 언급한 attention mechanism
||는 concatenation operation을 의미한다. softmax 함수로 인해 정규화된 attention coefficient는 linear combination에 사용된다.

좌측 그림의 경우 우리가 위에서 다룬 simple attention layer를 의미하고, 오른 쪽의 경우 attention layer가 3개인 경우를 의미한다. 서로 다른 색상의 attention layer를 계산하고 concatnation한 후 마지막에는 average를 통해 최종
이때 ||는 concatenation을 의미하고,
Comparison to related work
이번 섹션에서는 이전 연구에서 존재한 여러 문제를 GAT를 통해 해결한 내용에 대해서 다룬다.
Computationally
GAT에서 사용하는 self-attention layer는 모든 edge에 대해서 병렬적으로 처리가 가능하기 때문에 매우 효율적이다. 또한, GCN의 경우 eigendecomposition이나 이와 유사한 연산을 진행하기 때문에 많은 양의 연산이 요구되는 반면 GAT는 이러한 연산이 필요없기 때문에
different importance
위에서도 언급했듯 GAT는 각 node의 이웃에 대해서 서로 다른 가중치를 부여할 수 있다. 이는 모델 성능 개선에 효과적이며 서로 다른 가중치를 분석할 경우 기존의 모델에 비해 해석 가능성(interpretability)이 높아진다는 장점이 있다.
Share manner
Attention 메커니즘은 그래프의 모든 edge를 공유하는 형태를 가지고 있다. 기존 연구의 경우 Global graph structure(directed, undirected, etc..)이나 upfront access에 의존하지만, GAT의 경우 국한되지 않는다. 의존하지 않는 경우 training data에서는 보이지 않는 pattern에 대해서도 학습하는 것이 용이하며 undirected 구조가 아닌 경우에는
unfixed-size neighborhood
Hamilton이 2017년에 제안한 GraphSage의 경우 node에 대해 고정된 사이즈의 이웃을 고려하였다. 이는 inference 단계에서 이웃 전체에 대한 접근이 불가능하다. 추가적으로, 해당 논문의 실험 결과 LSTM-based 로 한 모델이 가장 우수한 성능을 발휘하였다. 해당 논문에서의 가정은 그래프에 일관된 Sequence 순서가 존재한다는 가정 하에 진행된 것이며 본 논문에서 제안하는 GAT의 경우 이와 같은 가정을 두고 진행하지 않고, 이전 방식과는 다르게 고정된 이웃을 고려하는 것이 아니라 전체 이웃에 대해서 계산을 진행한다.
particular instance of MoNet
본 논문은 MoNet의 구조의 특정 instance로 구성될 수 있다. 구체적으로, MoNet를 pseudo-coordinate function
Evaluation
GAT의 성능을 검증하기 위해 Cora, Citeseer, Pubmed, PPI 등의 데이터를 사용하고 다양한 모델과 성능을 비교하였다. 기본적인 데이터의 통계량은 다음과 같다.

Cora, Citeseer, Pubmed의 경우 Transductive Learning을 의미하고, PPI는 Inductive Learning을 의미한다. Transductive Learning은 그래프 상에서 일부 node와 edge의 ground truth를 아는 상태에서 나머지의 node, edge를 예측하는 semi-supervised learning을 의미한다. 반면에 Inductive Learning은 ground truth를 알고 있는 그래프에 대해서 먼저 학습한 후 전혀 새로운 그래프에 대해 node와 edge에 대해서 추정하는 우리가 알고 있는 일반적인 supervised learning의 형태를 의미한다.
Results
Transductive learning과 Inductive learning의 실험 결과는 다음과 같다.
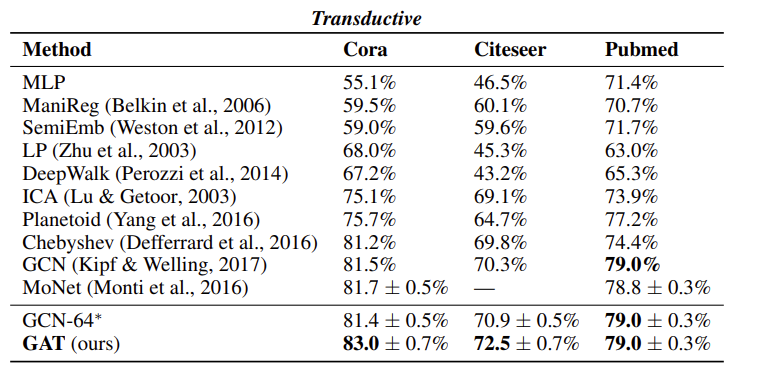
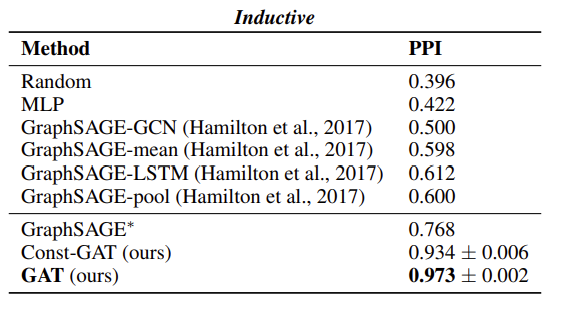
Transductive Learning의 경우 근소한 차이로 가장 우수한 성능을 발휘하고 있으나, Inductive Learning에서는 매우 우수한 성능을 보이고 있다. 이로써, GAT는 inductive learning에서 우수한 것을 검증하였다.
Conclusions
본 논문에서는 masked self-attentional layer를 활용하여 그래프 구조에서도 작동하는 Graph Attention Networks(GATs)를 제안하였다. GAT는 계산이 매우 효율적이며, 이웃 내의 다른 node의 중요도를 할당할 수 있다. 또한, 크기가 지정되거나 전체 그래프를 알아야 한다는 것에 의존하지 않기에 기존의 Spectral based 접근 방식에 많은 이론적 문제를 해결하였다. 또한, 실험 결과 Transductive, Inductive 모두 우수한 성능을 발휘하였다.
향후 더 큰 배치 크기를 처리할 수 있도록 하는 연구가 필요하며 interpretability를 향상시키는 것도 매우 흥미로운 연구 방향이 될 수 있다. 또한, node classification이 아닌 graph classification을 수행하는 것도 하나의 응용 연구에 적절하다. 마지막으로, 모델을 확장해 node 뿐만 아니라 edge까지 고려할 경우 더욱 다양한 문제를 해결할 수 있을 것으로 기대한다.