Simplifying Graph Convolutional Networks (PMLR'19)

Contents

• Abstract
• Introduction
• Simple Graph Convolution (SGC)
  • Graph Convolutional Networks
    • Feature propagation
    • Feature Transformation and nonlinear transition
    • Classifier
  • Simple Graph Convolution
    • Linearization
    • Logistic regression
  • Spectral Analysis
    • Preliminaries on Graph Convolutions

 

 

Abstract

GCN과 GCN을 변형한 다양한 모델들은 상당한 주목을 받아왔으며, 사실상(de facto) Graph Representation을 학습할 때 가장 좋다고 알려진 방법이다. GCN은 CNN을 기반으로 진행되는데, 이 방식은 불필요한 복잡성과 중복된 계산이 요구된다. 따라서, 본 논문에서는 비선형성을 제거하고, Layer 사이의 Weight Matrix를 축소함으로써 GCN이 가지고 있는 과도한 복잡성을 줄였다. 복잡도는 줄였지만 많은 다운스트림 태스크에서 정확도에 부정적인 영향을 주지 않는다는 것을 검증하였다. 또한, 더 큰 데이터셋으로 확장이 가능하고 해석 가능성이 높아지며, FastGCN에 비해 속도는 최대 2배 가량 향상되었다. 

 

Introduction

Simplifying Graph Convolutional Networks (ICML'19)는 이후 LightGCN의 기반이 되는 논문 중 하나이다. 기존에 다양한 GCN 관련 논문들이 제안 되었으나 반복적인 non-linear를 통해 복잡한 구조를 가지고 있었다. 머신러닝에서도 처음에는 선형성을 기반으로 MLP 등과 같이 복잡한 비선형성을 가진 모델을 가지고 성능을 개선시켰으나, non-linear 모델은 linear 모델에 비해 설명력이 떨어진다. 본 논문에서는 non-linear를 제거하고 linear transformation를 사용하는 Simple Graph Convolution (SGC)를 제안하였으며, SGC는 기존에 제안된 GCN 논문들에 비해 간단하면서도 동등하거나 혹은 그 이상의 성능을 발휘하는 것을 증명하였다. 또한, 기존의 non-linear 구조를 가진 GCN 과는 달리 직관적으로 해석이 가능하며 Graph Convolution 관점에서 이론적 분석을 제공한다. 

 

Schematic layout of a GCN and SGC

Simple Graph Convolution (SGC)

본 논문에서는 Kipf & Welling (2017)이 제안한 GCN을 기반으로 node classification에서의 SGC를 소개한다. 또한, 본 논문에서 제안한 renormalization trick 방법이 얼마나 효과적으로 Graph spectral domain을 축소하고  SGC에서 어떻게 low-pass-type filter가 되는지 보여준다. 

 

본 논문에서 사용하는 기호들의 설명은 다음과 같다. 

• Graph: $\mathcal{G}=(\mathcal{V},\mathit{A})$
• set of nodes: $\mathcal{V}=\{v_1,...,v_n\}$
• symmetric adjacency matrix: $\mathit{A}$
• attribute in $\mathit{A}$: $a_{ij}$ between node $v_i$ and $v_j$
• degree matrix: $\mathit{D}=\text{diag}(d_1,...,d_n)$
• $d_i=\sum _j{a}_{ij}$
• feature vector: $x_i\in {\mathbb{R}}^d$
• entire feature matrix: $\mathit{X}\in {\mathbb{R}}^{n\times d}$, $X=[x_1,...,x_n{]}^T$
• one-hot vector of classes: $y_i\in \{0,1{\}}^C$

 

 

 

Graph Convolutional Networks

CNN과 MLP와 유사하게 GCNs도 multi-layer를 통해 각 node의 feature $x_i$를 위한 새로운 feature representation을 학습한 결과를 linear classifier의 입력으로 사용한다. $k^{\text{th}}$ Conv Layer의 경우 모든 node의 representation을 $H^{(k-1)}$로 표현하고 출력되는 node의 representation은 $H^{(k)}$로 표현한다. 첫 번째 node representation은 input feature가 되며 아래와 같이 표기한다.

$$H^{(0)}=\mathit{X}$$

해당 값이 GCN layer의 첫 번째 input으로 사용된다. K-layer GCN은 K-layer MLP를 그래프의 각 node feature vector $x_i$에 적용하는 것과 동일하며, 각 노드의 hidden representation은 layer의 시작 부분에서 node의 이웃과 평균을 낸 값이다. 각각의 Graph Conv Layer는 node representation을 업데이트하기 위해 Feature propagation, Feature transformation, nonlinear transition, 총 3가지 단계로 구성된다. 

 

Feature propagation

해당 부분이 MLP와 GCN을 구별할 수 있는 부분이며, 각 Layer의 시작 부분에서 각 node $v_i$의 feature $h_i$는 주변 이웃 노드 feature vector의 평균을 통해 계산된다. 

$${\overline{h}}_i^{(k)}\leftarrow \frac{1}{d_i+1}{h}_i^{(k-1)}+\sum _{j=1}^n\frac{a_{ij}}{\sqrt{(d_i+1)\cdot (d_j+1)}}{h}_j^{(k+1)}$$

위 수식에서 self-loop를 포함한, 즉, 'normalized'한 수식과 이를 행렬식으로 간단하게 표현하면 수식은 아래와 같다. 

$$S={\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}$$

$${\overline{H}}^{(k)}\leftarrow S{H}^{(k-1)}$$

이 과정을 통해 node의 hidden representation을 smooth하게 만든다. 

 

Feature Transformation and nonlinear transition

smoothing을 한 후, GCN Layer는 MLP Layer와 동일한 형태로 진행된다. 각각의 Layer는 Weight Matrix ${\mathrm{\Theta }}^{(k)}$로 연결되어 있으며, Layer의 값과 Weight Matrix를 곱함으로써 선형 변환을 한다. 

$$H^{(k)}\leftarrow \text{ReLU}\left({\overline{H}}^{(k)}{\mathrm{\Theta }}^{(k)}\right)$$

 

Classifier

마지막으로 Classifier를 통과해 node classification을 수행한다. 이때 Softmax classifier를 사용하며, node의 수가 n인 경우에는 $\hat{Y}\in {\mathbb{R}}^{n\times C}$가 된다. 

$${\hat{Y}}_{\text{GCN}}=\text{softmax}\left(S{H}^{(K-1)}{\mathrm{\Theta }}^{(K)}\right)$$

$\text{softmax}(x)=\exp (x)/\sum _{c=1}^C\exp (x_c)$를 의미한다. 

 

Simple Graph Convolution

전통적인 MLP는 Layer를 거칠수록 보다 고차원의 데이터를 얻을 수 있다. 반면에, GCN는 Layer를 거치면 다음 hop의 정보를 얻는다. 이 효과는 receptive field를 증가시키는 Conv Layer와 유사한 구조를 띄고 있다. Conv Layer의 경우 VGG나 ResNet만 보더라도 Layer를 깊게 쌓을수록 우수한 성능을 발휘하는 반면, MLP의 경우에는 3, 4 Layer를 넘어가면 별다른 이점이 존재하지 않는다. 

 

Linearization

GCN은 MLP와도 유사하고 CNN과도 유사하다. 기존의 GCN은 CNN과 같은 형태로 Layer를 쌓는 구조를 띄었으나 Layer를 쌓을수록 성능이 저하되는 것을 확인할 수 있다. 따라서, 본 논문에서는 non-linear이 그다지 중요하지 않다는 것을 가정으로 한다. 그러나, 대부분의 benefit은 local averaging에서 발생하기 때문에, Layer 사이의 non-linear는 삭제하고 마지막 softmax 함수는 살려둔다. 

$$\hat{Y}=\text{softmax}(S...SSX{\mathrm{\Theta }}^{(1)}{\mathrm{\Theta }}^{(2)}...{\mathrm{\Theta }}^{(K)})$$

K-th normalized matrix $S$를 $S^K$로 표현하고, $\mathrm{\Theta }={\mathrm{\Theta }}^{(1)}{\mathrm{\Theta }}^{(2)}...{\mathrm{\Theta }}^{(K)}$로 표현하면 최종 수식은 아래와 같이 표현된다. 

$${\hat{Y}}_{\text{SGC}}=\text{softmax}(S^{K}X\mathrm{\Theta })$$

 

Logistic regression

$\overline{X}=S^{K}X$로 표현하면, $\hat{Y}=\text{softmax}(\overline{X}\mathrm{\Theta })$는 $\overline{X}$에 대한 Weight를 계산할 필요가 없기 때문에 multi-class Logistic Regression으로 축소할 수 있다. 

 

Spectral Analysis

이번 장에서는 SGC를 Graph Convolution 관점에서 다룬다. 본 연구에서는 SGC가 Spectral domain의 fixed filter에 해당하는 것을 검증하였다. 이때, SGC는 그래프에서 low-pass filter의 역할을 어떻게 수행하는지 알아보자.

 

Preliminaries on Graph Convolutions

Graph Fourier analysis는 Euclidean domain과 유사하게 Spectral decomposition (Graph Laplacian)에 의존한다. Graph Laplacian은 $\mathrm{\Delta }=D-A$로 정의되며, normalized versiond은 ${\mathrm{\Delta }}_{sym}=D^{-1/2}\mathrm{\Delta }{D}^{-1/2}$로 표현한다. 이때 $\mathrm{\Delta }=U\mathrm{\Lambda }{U}^T$는 양의 준정부호 대칭 행렬을 의미한다. 이때 $\text{x}$의 Fourier Transform은 $U^T\hat{\text{x}}$ 로 표현할 수 있으며, 역변환은 $\text{x}=U\hat{\text{x}}$로 표현할 수 있다. 따라서, Graph Convolution Operation은 아래와 같이 표현할 수 있다. 

$$\text{g * x}=U((U^{\text{g}})\odot (U^T\text{x}))=U\hat{G}{U}^T\text{x}$$

위 수식을 k-th order polynomial(Chebyshev)로 변형하면 아래와 같은 수식으로 표현이 된다. 

$$\text{ g * x}=\theta (I+D^{-1/2}A{D}^{-1/2})\text{x}$$

최종 설계된 모형은 기존의 GCN 논문에서 제안된 renormalized trick을 사용한 모델이다. 이와 같이 일반화 함으로써 Layer를 여러 층으로 쌓을 수 있게 되었다. 

 

SGC and Low-Pass Filtering

본 논문에서는 SGC가 GCN의 Low Pass Filtering임을 보여준다. 이때 Loss Pass Filtering은 말그대로 낮은 주파수만 통과한다는 것을 의미한다. 이때의 낮은 주파수는 eigenvalue가 낮은 것을 의미한다. 먼저 initial first-order Chebyshev filter는 GCN으로 파생되었기 때문에 propagation matrix는 ${\mathit{S}}_{\text{1-order}}=I+D^{-1/2}A{D}^{-1/2}$가 된다.

 

${\mathrm{\Delta }}_{\text{sym}}=I-D^{-1/2}A{D}^{-1/2}$이기 때문에 이를 이전 수식에 대입하면 ${\mathit{S}}_{\text{1-order}}=2I-{\mathrm{\Delta }}_{\text{sym}}$이 된다. 그러므로, ${\mathit{S}}_{\text{1-order}}^K$이면 filter coefficient는 ${\hat{g}}_i=\hat{g}({\lambda }_i)=(2-{\lambda }_i{)}^K$가 된다. 아래의 그림에서 관찰되는 바와 같이 First-Order Chebyshev는 eigenvalue가 1보다 작을 때 필요 이상으로 신호를 증폭시킨다는 문제점이 존재한다. 이와 같은 문제를 해결하기 위해 기존의 GCN은 renormalized trick을 사용하였다.

 

renormalized trick은 모든 노드에 대한 self-loop를 normalized adjacency matrix에 더해주는 것을 의미한다. ${\tilde{\mathit{S}}}_{\text{adj}}={\tilde{D}}^{-1/2}\tilde{A}{\tilde{D}}^{-1/2}$가 되며, ~는 self-loop를 더해준 것을 의미한다. 즉, $\tilde{A}=A+I,\tilde{D}=D+I$를 의미한다. 이때는 이전과는 달리 $\hat{g}({\tilde{\lambda }}_i)=(1-{\tilde{\lambda }}_i{)}^K$가 된다. renormalized trick을 사용하면 Spectral Coefficient를 축소시킬 수 있는 것을 확인할 수 있다. 

 

 

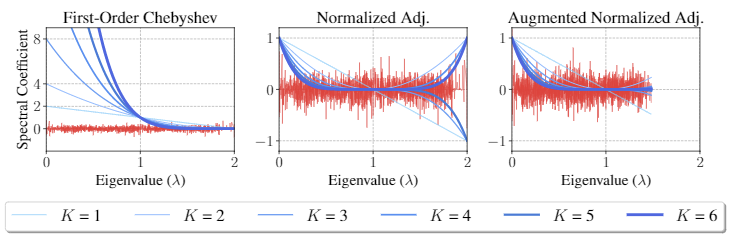
마지막 그림의 Augmented Normalized Adj.는 ${\tilde{\mathit{S}}}_{\text{adj}}={\tilde{D}}^{-1/2}\tilde{A}{\tilde{D}}^{-1/2}$를 의미한다. 원래의 spectral 의 범위는 [0,2]를 가진다. 이때 ${\lambda }_i$가 1보다 큰 경우에 차수가 홀수가 되면 $(1-{\lambda }_i{)}^K$ 홀수 차수일 때마다 음수의 값을 도출한다. 이때 self-loop를 더해준 ${\tilde{\mathit{S}}}_{\text{adj}}$는 가장 큰 고유값이 2에서 1.5로 줄어들기 때문에 음의 계수의 영향력이 줄어든다. 나아가, 이처럼 스케일링 된 spectrum은 ${\tilde{\mathit{S}}}_{\text{adj}}$로 정의된 필터가 low-pass-filer로 작동하는 것으로 이해할 수 있다.