Contents
기존 Data Augmentation 방식은 Heuristic하게 적용하기 때문에 도메인에 따라 성능이 달라진다는 문제점이 존재한다. 본 연구에서는 Fairness-aware한 방식을 통해 Data Augmentation을 수행하는 Graphair 기법을 제안하였다.
Introduction
Graph Neural Network (GNN) 기법은 Knowledge Graph, Social Media, Molecular Prediction 등과 같은 다양한 분야에서 우수한 성능을 보이고 있다. 그러나, 대부분의 GNN 기법은 인종, 성별 등과 같은 민감한 정보에 따라 다른 예측값을 도출하는 문제가 존재한다. 이와 같은 문제를 해결하고자 Node Feature Masking, Edge Perturbation 등과 같은 Heuristic Data Augmentation 방법을 주로 사용하는데, 이와 같은 방법은 도메인에 따라 서로 다른 결과가 도출된다는 단점이 존재한다.
따라서 본 연구에서는 Heuristic Data Augmentation 방식이 아닌 Automated Data Augmentation 방식인 Graphair 기법을 제안하고자 한다. Graphair의 핵심은 Fairness와 Informativeness를 같이 향상시키기 위해 Adversary Model과 Contrastive Learning 기법을 사용한다.
Background and Related Work
Fair Graph Representation Learning
본 연구에서는 그래프
연구의 목적은 Fiar Graph Representation Model
Fairness via Automated Data Augmentations
본 연구에서는 새로운 그래프
먼저 Edge Perturbation은 Embedding
Node Feature Masking은 Embedding
그러나, Bernoulli Distribution과 Mask Matrix
Adversarial Training
본 연구에서의 목적은 편향을 줄이기 위해 Fair Agumentation을 생성하는 것이다. 따라서, Augmentation Model
이때 본 연구에서 사용하는 Adversary Model과 Augmentation Encoder
Contrastive Learning
마지막으로 Contrastive Learning을 사용하였다. 이번 단계는 Node Representation
최종 Contrastive Learning의 Loss Function은
본 연구에서는 Augmentation Model
위 전체 과정을 종합하여 최종 Loss Function은 아래와 같이 정의할 수 있다.

Experiments
본 연구에서는 Fiarness와 Informativeness에 대한 성능을 검증하기 위해 Accuracy와 Demographic Parity
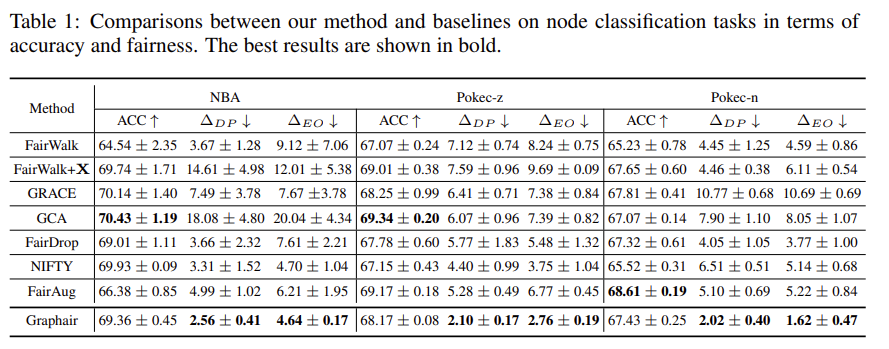
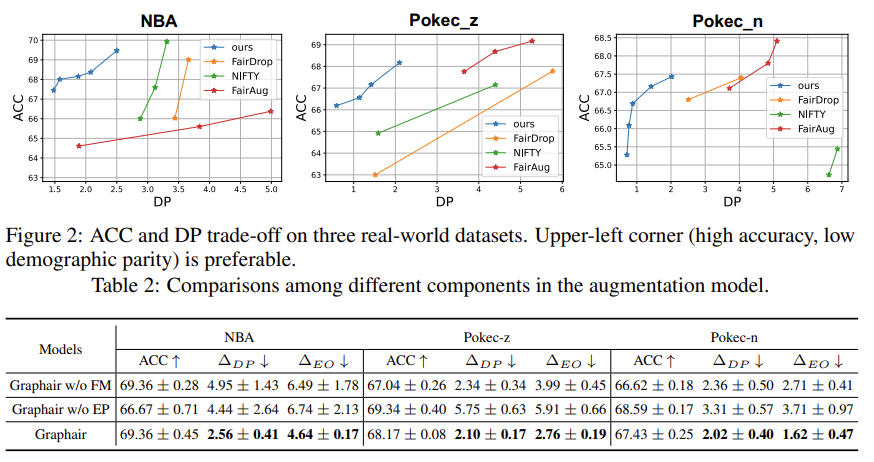
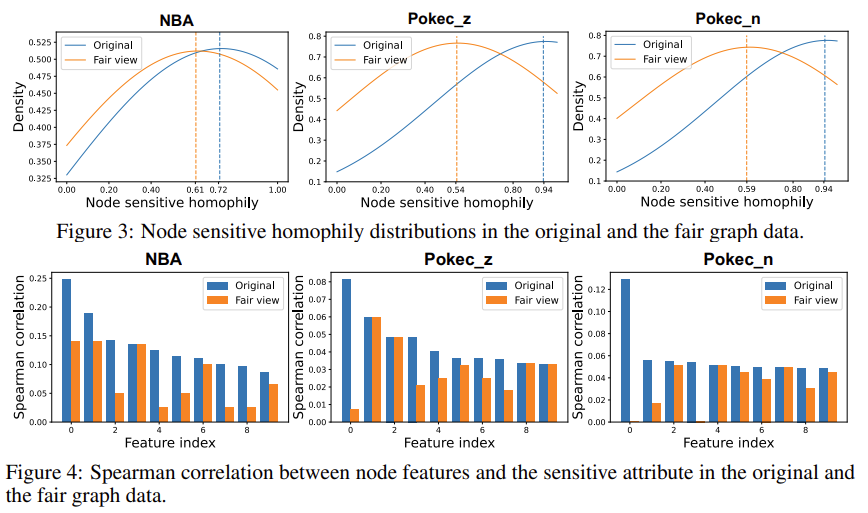
Baseline Model은 Fairwalk, Fairwalk + Node Feature, GRACE, GCA, NIFTY, FairDrop, FairAug를 사용하고, NBA, Pokec_z, Pokec_n 데이터를 사용하였다. 실험은 1) Experimental Results, 2) Ablation Studies, 3) Analysis of Fair View 총 3가지로 구성하였다. 먼저, Experimental Results에서는 Fairness와 Accuracy Performance는 Trade-off 관계에 있다는 것을 시각화하고, 본 연구에서 제안하는 Graphair 기법과 다른 Graph 기반 기법 간의 성능 및 Fairness를 비교분석한 실험이다 (Figure 2, Table 1). Ablation Studies는 본 연구에서 제안하는 Graphair 기법 내에 Feature Mask (FM), Edge Perturbation (EP)를 제거했을 때 모델의 성능을 비교분석한 실험이다 (Table 2). Analysis of Fair View는 Node Sensitive Homophily를 보여주고 Node 간의 Spearman Correlation을 보여준다. 기존 선행 연구에 따르면 Node Sensitive Homophily가 높을수록 Prediction Bias가 발생한다고 한다. 본 연구의 기법은 다른 기법에 비해 Node Sensitive Homophily가 낮은 부분에 Density가 높기 때문에 상대적으로 Prediction Bias가 낮다고 볼 수 있다.
'Paper review > Graph Mining' 카테고리의 다른 글
| Model Degradation Hinders Deep Graph Neural Networks (KDD'22) (0) | 2022.09.20 |
|---|---|
| Graph Attention Networks (ICLR'18) (1) | 2022.07.26 |
| Simplifying Graph Convolutional Networks (PMLR'19) (0) | 2022.07.19 |
| Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering (NeurIPS'16) (1) | 2022.07.07 |
| Semi-Supervised Classification With Graph Convolutional Networks (ICLR'17) (0) | 2022.06.15 |