Contents
Walk, Trail 등 다양한 구조를 가진 그래프가 존재한다. 본 글에서는 각 그래프에 해당하는 이름에 대해서 살펴보고 해당 그래프의 특징을 알아보고자 한다. 먼저 Walk를 다루기 이전에 그래프에서의 Length가 어떤 것인지 알아보자.
Length
Length는 그래프의 길이를 의미한다. 노드의 개수가 아닌 엣지들이 지나가는 길의 수를 의미하는 것이며, 이를 Hop이라고 한다. $V_5$에서 $V_1$까지는 총 2-hop을 나타내고, $V_5$에서 $V_3$까지는 3-hop을 나타낸다.

그렇다면 Hop의 수는 어떻게 구할 수 있을까?
Walk
보행(Walk)은 복잡하게 보이지만, 그래프의 노드를 통과하는 하나의 스텝(step)일 뿐이다.


Walk는 움직일 때 거치는 엣지의 수를 의미한다. 왼쪽 그림의 경우 $a \rightarrow b \rightarrow c \rightarrow d \rightarrow b$로 움직였다고 한다면, 이때의 Walk는 4가 된다. 4개의 엣지를 거쳤기 때문이다. Walk는 Closed Walk와 Open Walk로 나뉘뉜다. Closed Walk는 시작 노드와 끝나는 노드가 같은 경우($v_o = v_k$)를 의미한다. 시작 노드와 끝나는 노드가 같지 않으면 전부 Open Walk라 부른다.
Trail, Path, Cycle, Circuit
Trail과 Path는 Walk의 한 종류라고 볼 수 있다. Trail은 엣지가 반복되지 않는 Walk를 의미하고, Path는 Trail이면서 노드가 반복되지 않는 Walk를 의미한다. 각각의 Path들이 연결된 엣지가 없는 경우 Independent Path라고 한다. 이 때 노드는 연결된다고 하더라도 Independent Path라고 한다. 이때 A에서 B로 가는 Independent Path의 upper bound, 즉, 상한은 두 노드의 차수의 수를 넘을 수 없다. 이때 node independent 한 경우에는 edge independent하지만 역은 성립하지 않는다.


왼쪽 그림의 경우 $a \rightarrow b \rightarrow c$로 엣지가 겹치지 않는다. 반면에, 오른쪽 그림의 경우 경로를 따라 움직이기 위해서는 엣지가 중복되어야 한다. 따라서 Trail이 아닌 Walk 다.

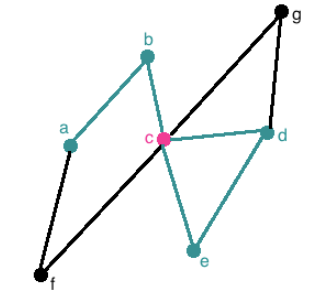
왼쪽 그림은 시작 노드와 끝 노드가 겹치지 않으며, 노드가 중복되지 않는다. 따라서, Open Walk이자 Path가 된다. 오른쪽 그림은 $c$ 노드가 겹치고 있기 때문에 Walk다.
Trail의 특수한 케이스는 Path 뿐만 아니라 Cycle과 Circuit도 존재한다. Cycle은 Closed Trail이라고도 부르며, 시작 노드와 끝 노드가 반복되는 것을 말한다. Circuilt도 역시 Closed Trail이라 부르며, 엣지는 반복되지 않지만 노드는 많이 반복되는 그래프를 의미한다.


Connected Component, Connected Graph
연결 요소(Connected Component)는 그래프가 주어졌을 때 나머지 그래프에서 주변 노드에 인접하지 않는 경우를 의미한다. 아래의 그림을 참고하면 각각의 Path와 Circle 들을 Connected Component라고 부른다.

반면에, 연결 그래프(Connected Graph)는 모든 요소들이 연결되어 있는 그래프를 의미한다. 위의 그림은 2개의 구성 요소를 가지고 있기 때문에 연결 그래프가 될 수 없다. 따라서, 모든 노드들은 연결되어 있어야 한다.

위 그림의 경우 하나의 구성 요소를 가지고 있기 때문에 연결 그래프라고 할 수 있다. 그렇다면 이때 최단거리(Shortest path)는 얼마인가? $V_1$에서 $V_5$로 가는 경우의 최단 거리는 1이다. $V_1$에서 $V_6$의 최단거리는 2이다. 이 그래프의 지름(Diameter)은 얼마일까? 지름 최단거리 중에서 가장 길이가 긴 값을 의미한다. $V_6$에서 $V_3$으로 가는 최단거리가 가장 긴 거리인 4일 것이다. 따라서 위 그래프의 지름은 4가 된다.
'Deep Learning > Graph Neural Network' 카테고리의 다른 글
| [Graph] Measuring Network (1) | 2022.09.30 |
|---|---|
| Node Embedding (0) | 2022.09.02 |
| Community Detection (0) | 2022.09.02 |
| Graph를 이용한 Cascade 모델링 (0) | 2022.09.02 |
| Link Prediction with DGL (0) | 2022.09.01 |