[Graph] Measuring Network

Contents

• Density

 

 

네트워크에는 밀집(Density), 차수(Degree), 길이(Length) 등 다양한 지표가 존재하며, 이를 측정하기 위한 방법도 다양하게 존재한다. 본 글에서는 이를 측정하는 방법에 대해서 알아본다. 

 

Density

Density는 그래프의 밀집 정도를 의미한다. 예를 들어, 완전 연결 그래프의 경우 Density는 1이 될 것이다. 완전 연결 그래프는 Complete Graph 혹은 Clique로 부르기도 한다. 이때 평균 차수는 다음과 같이 계산할 수 있다.

$$m=\left(\begin{array}{c}n\\ 2\end{array}\right)=\frac{n(n-1)}{2}$$

$$⟨k⟩=\frac{2m}{n}=\frac{n(n-1)}{2}=n-1$$

그래프의 Density는 $\rho$로 표기할 수 있으며, $\rho$는 아래와 같이 평균 차수 $m$으로 계산이 가능하다.

$$\rho =\frac{m}{{}_n{C}_2}=\frac{2m}{n(n-1)}=\frac{⟨k⟩}{n-1},(0\le \rho \le 1)$$

$$\rho =\frac{⟨k⟩}{n}$$

만약 $n$이 엄청 크다면, $n-1$은 $n$이 되기 때문에 위 수식처럼 변환이 가능하다. 실제 데이터는 n이 크기 때문에 성립된다. 

 

Clustering Coefficient 

군집 계수는 노드 $i$의 이웃들이 연결되어 있는 정도를 의미한다. 예를 들어, 이웃끼리 연결성이 높다면 Clustering Coefficient는 높아진다. 

$$c_i=\frac{e_i}{\left(\begin{array}{c}{k}_i\\ 2\end{array}\right)}=\frac{2e_i}{k_i(k_i-1)}$$

$k_i$는 차수를 의미한다. $e_i$는 전체 undirected edge를 의미한다. $c_i$는 1에 가까울수록 높은 것을 의미하며, $c_i\in [0,1]$이 된다. 

 

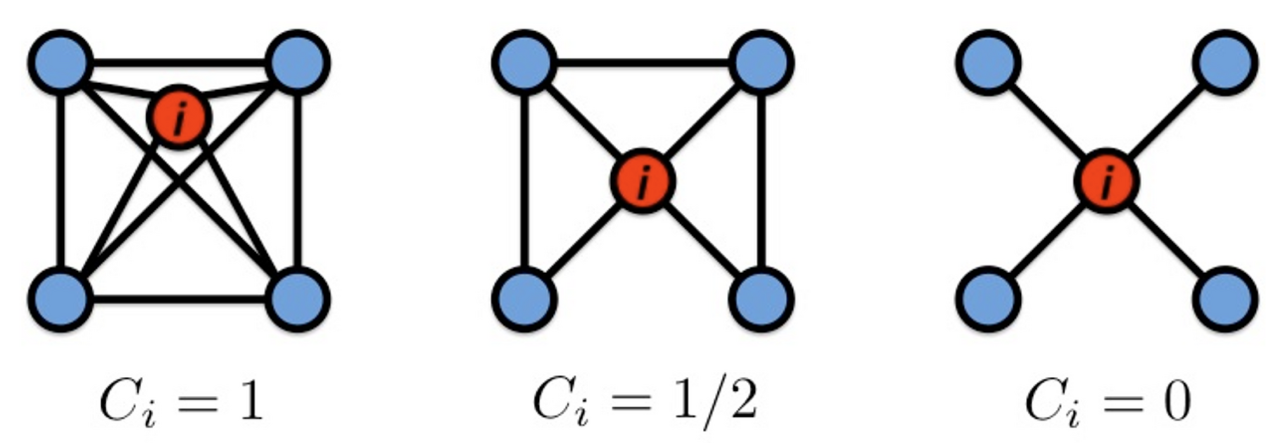
첫 번째의 경우 $c_i=\frac{2\ast 6}{4\ast 3}=1$이 된다. 두 번째의 경우 $c_i=\frac{2\ast 3}{4\ast 3}=\frac{1}{2}$가 된다. 위 경우에는 한 노드에 대한 Clustering Coefficient를 계산했다. 전체 노드에 대한 Coefficient는 아래와 같이 계산이 가능하다.

$$⟨C⟩=\frac{1}{n}\sum _i^n{c}_i,\text{where }{c}_i=\frac{2e_i}{k_i(k_i-1)}$$

위 Clustering Coefficient는 Local하게 측정한 값이다. Global Level에서 Clustering Coefficient를 계산하는 것은 Transitivity라고 한다. Transitivity는 Global한 정보를 보기 때문에 이웃의 이웃이 나와 이웃인지 등의 정보까지 고려하게 된다.

$$c=\frac{(\text{\#triangles})\times 3}{(\text{\#connected triples})}=\frac{\sum _{ijk}{A}_{ij}{A}_{jk}{A}_{ki}}{\sum _{ijk}{A}_{ij}{A}_{jk}}$$