Contents
Lecture 1.3에서는 Graph Representation를 고르는 방법에 대해서 다룬다. 먼저 Graph Representation을 알기 전 Graph의 구성에 대해서 먼저 알아보자. 그래프는 Nodes, Vertice로 불리는 Objects와 Links, Edges로 불리는 Interactions, 그리고 Network, Graph로 불리는 System로 구성되어 있다. Node로 표현할 경우 $N$, Vertices로 표현할 경우 $V$로 표기한다. Interaction의 경우 주로 Edge로 표현하며 $E$로 표기하고 System은 $G(N,E)$로 표기한다.

Graph는 일반적으로 사용자와 사용자 간의 관계를 표현할 때 사용하거나 프로틴(Protein)과 같은 분자 구조를 표현할 때도 사용된다. Graph는 한 분야에서만 사용되는 것이 아니라 다양한 분야에서 사용되기 때문에 분야에 맞는 Graph Representation을 선택하는 것이 매우 중요하다. 데이터가 주어졌을 때 우리는 그래프로 어떻게 디자인할 것인지 결정해야 한다. 이때 가장 좋은 성능을 발휘할 수 있는 Graph Representation을 어떻게 선택할 수 있을까? 어떤 경우에서는 unique하고 unambiguous representation이 존재한다. 다른 경우에는 unique한 representation이 존재하지 않을 수도 있다.
Directed vs Undirected Graph
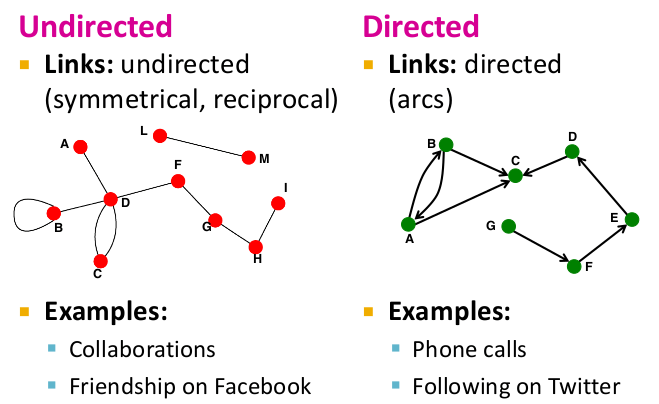
내가 Edge를 할당하는 방식에 따라 어떤 방식으로 접근해야 되는지 결정된다. Edge는 방향성이 존재하지 않는 Undirected Edge(Symmetrical, reciprocal)와 방향성이 존재하는 Directed Edge(arcs)가 존재한다. Collaboration, Frendship on Facebook과 같은 경우가 Undirected에 속하고, Phone Call, Following과 같은 경우가 Directed에 속한다.
Node Degrees
Degree는 차수를 의미하며, Undirected에서는 Node에 인접(adjacent)해 있는 Edge의 수를 의미한다. 만약 노드 $A$에 인접한 Edge가 4인 경우는 $k_A=4$로 표현한다. Undirect 그래프의 모든 노드의 평균 차수를 구하는 식은 다음과 같다.
\[ \bar{k} = \left\langle k \right\rangle = \frac{1}{N} \underset{i=1}{\overset{N}{\sum}}k_i = \frac{2E}{N} \]
Edge는 Node와 Node를 이어주는 역할을 한다. 즉, 하나의 Edge는 2개의 Node와 접해있는 것이다. 따라서, Degree를 연산할 때 $E$에 2를 곱하고, $N$으로 나누어 줌으로써 평균 Degree를 구할 수 있다. 반면에 Directed에서는 방향성이 존재하기 때문에 Node로 들어오는 incoming degree와 Node에서 나가는 outcoming degree가 존재한다. 따라서 Undirected와는 조금 다른 수식을 가지고 있다.
\[ \bar{k} = \frac{E}{N}, \bar{k}^{in} = \bar{k}^{out} \]
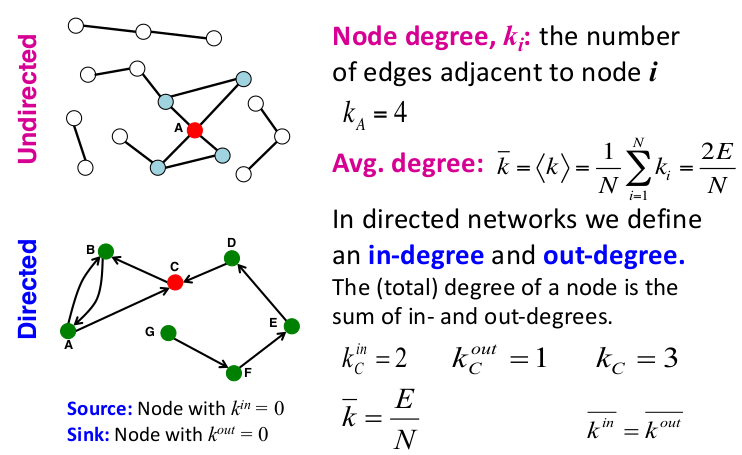
이때 $k^{in}=0$인 경우를 Source라고 부르고, $k^{out}=0$인 경우를 Sink라 부른다.
Bipartite Graph
Bipartite Graph는 매우 자주 접하는 Graph의 종류일 것이다. Node를 $U$와 $V$로 분리하고, $U$, $V$ 그룹 내의 Node끼리는 연결성이 존재하지 않는다면 이를 Bipartite Graph, 이분 그래프라고 부른다. 일반적으로 추천 시스템에서 사용자와 아이템 간의 interaction을 표현할 때 주로 사용된다. 사용자를 Node로 표현하고 User-Item Interaction을 Edge라고 한다면, 사용자와 사용자 간에는 Edge가 존재하지 않고, 마찬가지로 아이템과 아이템 간에도 Edge가 존재하지 않기 때문이다.

Folded/Projected Graph
Folded or Projected Graph는 Bipartite Graph의 Node Group을 분할한 Graph라고 한다. 하나의 side(left or right)의 두 Node가 적어도 하나의 공통된 neighbor를 공유할 경우에 Edge를 연결하는 형태로 Folded/Projected Bipartitle Graph를 그릴 수 있다. 위에서 언급한 Bipartite Graph는 $U$와 $V$만을 사용해서 Projection U와 Projection V를 만들 수 있다. 이때 Projection V의 경우를 예로 들자면, $B, C, D$ 간에는 하나의 공통된 Neighbor이 존재하지만, $A$와 $C, D$사이에는 공통된 Neighbor이 존재하지 않아서 Edge가 없다.

Adjacency Matrix
Adjacency Matrix는 $N_i$와 $N_j$ 사이에 Edge가 존재하는 경우에는 1로 표현하고, 존재하지 않는 경우에는 0으로 포현한다. 각각의 Node에 대해서 동일한 방법을 사용하고, 이를 Matrix로 표현한 것이다. Undirected Graph의 경우 Matrix가 Symmetric하지만, Directed Graph의 경우에는 Sysmetric하지 않을수도 있다.

$ \text{Undirected} $
\[A_{ij} = A_{ji}, \ \ A_{ii}= \boldsymbol{O} \]
\[k_i = \sum^N_{j=1} A_{ij}, k_j = \sum^N_{i=1} A_{ij}, \ \ L = \frac{1}{2} \sum^N_{j=i} k_{i} = \frac{1}{2}\sum^N_{ij} A_{ij} \]
$ \text{Directed} $
\[ A_{ij} \neq A_{ji}, \ \ A_{ii} = \boldsymbol{O} \]
\[k^{out}_i = \sum^N_{j=1} A_{ij}, k^{in}_j = \sum^N_{i=1} A_{ij}, L= \sum^N_{i=1} k^{in}_i = \sum^N_{j=1} k^{out}_j = \sum^N_{j=1} A_{ij} \]
Adjacency Matrix의 각 행과 열은 Node들을 의미하며, Node가 4개인 경우 $4\times 4$ Square Matrix를 생성한다. Matrix $A$에 대해서 $A_{ij}=1$인 경우는 $N_i$와 $N_j$가 인접한 것을 의미한다. 즉, 두 Node 사이에 Edge가 존재한다는 것을 의미한다.
$N_i$와 $N_j$를 연결하는 Edge는 Tuple 형태로 표시한다. 예를 들어 $N_A$과 $N_B$와의 연결을 나타내는 Edge인 경우에는 (A, B)로 표기하며, 이를 Edge list라고 부른다. 그래프에는 Edge list 뿐만 아니라 Adjacency에 대한 list도 존재한다. Adjacency list는 아래와 같이 표현할 수 있다.
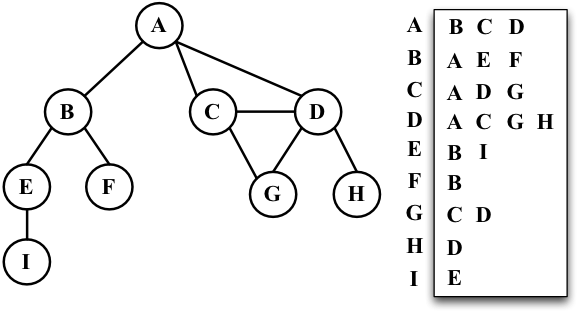
Adjacency를 list 형태로 생성하게 되면 Node가 주어졌을 때 인접한 Node를 검색하는 속도가 매우 빨라지게 된다. Undirected인 경우에는 양쪽 Node를 저장하면 되고, Directed 인 경우에는 incoming과 outcoming을 나누어서 list에 저장해주어야 한다.
Node and Edge Attributes
Weight
Weight는 Edge에 관련된 속성 중 하나이며, 얼마나 관련되어 있는지를 나타낸다. Undirected Graph의 경우 Weight가 높을수록 굵은 Edge로 표현하며, Weight에 따라 Adjacency의 Entity가 변경된다.
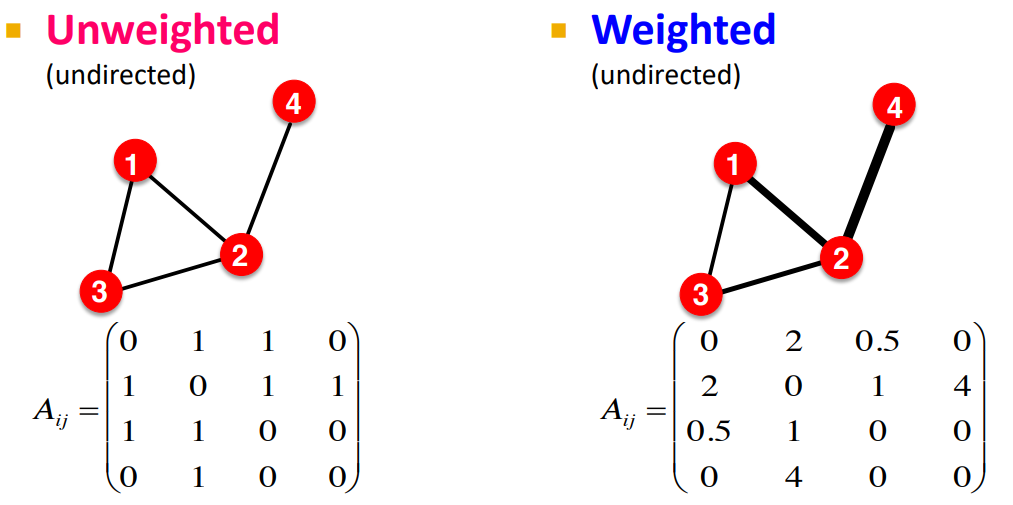
Self-Edges, Multigraph
지금까지의 Graph는 직선 Edge에 대해서만 다루었다. 그러나 실제 Field에서는 $A_{ii}$가 존재할 수도 있고, 두 Node 사이에 두 개 이상의 Edge가 존재할 수도 있다. 전자의 경우는 Self-Edge 혹은 Self-loops라 부르고, 후자의 경우는 Multigraph라 부른다.
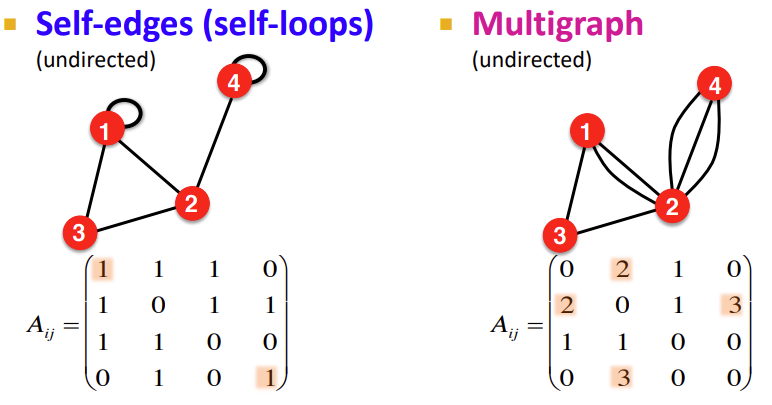
Multigraph는 실제 Field에서 주로 볼 수 있는 Graph 중 하나이다. 예를 들어, 친구 사이의 전화 통화나 사용자의 구매 기록 등과 같은 데이터를 이용할 때에는 하나의 Edge가 아니라 여러 개의 Edge가 존재하기 때문이다.
Connected, Unconnected
지금까지 다룬 Graph는 모두 Connected Graph다. Unconnected Graph는 Node가 서로 떨어져 있는 Node가 존재하는 Graph를 의미하며, Node에 연결된 Edge가 하나도 없는 Node는 Isolated Node라고 부른다. 이때 Edge가 가장 많이 연결된 Graph는 Giant Component라 부른다.
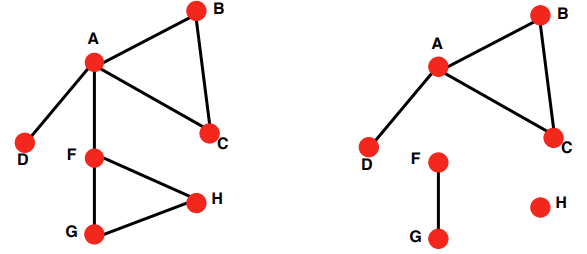
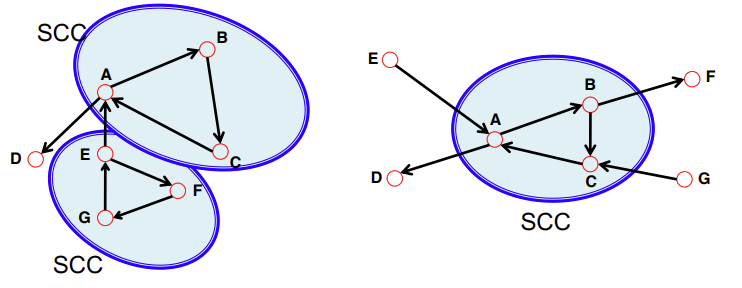
오른쪽 그림을 예로 들면, $N_H$가 Isolated Node를 나타내고, A,B,C,D로 연결된 Component를 Giant Component가 된다. Directed Graph에서는 Connected도 Strongly Connected와 Weakly connected 로 나눈다. Strongly Connected Components(SCCs)는 Cycle 구조를 가진 Connection인 경우를 의미한다. 그 외 경우는 Weakly Connected라 부른다.
Summary
- Choice of a graph representation
- Directed, Undirected
- Bipartite
- Weighted
- Adjacency Matrix
- Connected, UnConnected
- Strongly Connected, Weakly Connected
'Deep Learning > CS224W' 카테고리의 다른 글
| [CS224W] Node Embeddings (0) | 2022.07.05 |
|---|---|
| [CS224W] Traditional feature-based methods: Graph-level features (0) | 2022.07.04 |
| [CS224W] Traditional feature-based methods: Link-level features (2) | 2022.07.03 |
| [CS224W] Traditional feature-based methods: Node-level features (0) | 2022.05.17 |
| [CS224W] Application of Graph ML (0) | 2022.05.16 |