Contents
이전 Lecture에서 Node Level, Link Level, Graph Level을 활용한 케이스에 대해서 다루어 보았다. 이번 Lecture에서는 각각의 Level에서의 Prediction 방법에 대해서 다루고 있다.

각각의 Level에 대해서 Prediction을 하기 위해서는 일단 먼저 Node, Link, Graph 등의 feature를 생성하는 것부터 시작이다. 이번 Lecture에서는 전통적인 ML Pipeline을 구축해 Graph를 구축하고 있다. 전통적인 ML은 2 단계로 구성 되어 있다. 첫번째 단계는 먼저 Node, Link, Graph의 feature를 vector 형태로 가져오는 것이다. 그 후 Random forest, SVM, Feed Forward Neural Network (FFNN) 등의 모델을 학습한다.
Feature Design
Graph에서 효과적으로 Feature를 추출해 사용하는 것은 성능 개선에 있어 매우 중요한 부분이다. 이번 Lecture에서는 Classic ML를 학습하는 과정을 다룬다. Classic ML의 경우 feature를 수작업으로 변환하여 사용하는데, Nodel-level, Link-level, Graph-level을 예측할 때 어떤 방식으로 feature를 변환하는지 알아보자.
ML in Graph는 Graph $G = (V,E)$가 주어졌을 때 $f: V \rightarrow \mathbb{R}$을 학습하는 것이다. 그렇다면 $f$를 어떻게 학습할 수 있을까? 학습하는 방법은 각 Level에 따라 조금씩 다르다. 이번 글에서는 Node-Level에 대해서만 다룬다.
Node-level Tasks
Node Classification에서는 색칠이 되어 있지 않는 Node의 색을 예측하는 형태로 진행된다. 초록색을 0, 빨간색을 1로 설정하는 경우는 Binary Classification problem이다. 아래의 그림의 색이 칠해진 Node를 살펴보면 초록색 Node의 경우 적어도 2개 이상의 Edge가 연결되어 있다. 빨간색 Node의 경우 적어도 1개 이상의 Edge가 연결되어 있다. 이러한 패턴을 찾아 회색 Node의 색을 분류하면 오른쪽과 같은 그림이 된다.
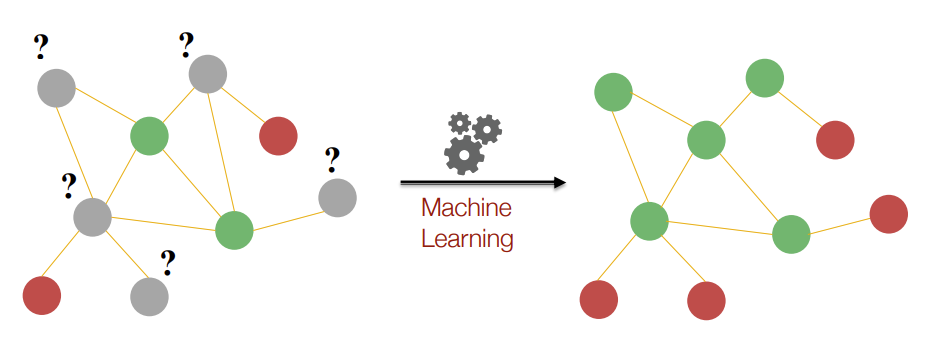
이때 topological한 부분에서 패턴을 설명할 수 있는 feature가 필요하다. Nodel-Level Feature는 Node의 구조와 위치를 특성화(Characterize)하는 것이 목적이다. 구조와 위치를 특성화 하는 방법은 다음과 같다.
- Node Degree
- Node Centrality
- Clustering Coefficient
- Graphlets
Node Degree
Node Degree는 Node의 차수를 의미하며, 노드에 연결된 Edge의 수를 정량적으로 표현한 것이다. 이는 매우 간단하지만 주로 사용되는 구조 중 하나이다.

이 경우 Node의 Degree가 같은 경우 구별하지 못한다는 단점이 존재한다. 예를 들어, $k_C$와 $k_E$는 동일한 Degree를 가지고 있으면 Classifier는 이를 구별하지 못한다. 또한, A, H, G, F는 동일한 Degree를 가지고 있기 때문에 Classifier는 같은 값으로 예측하게 된다.
Node Centrality
Degree는 Node의 중요도와 상관없이 단순히 Neighboring node의 수를 기반으로 Node의 feature를 생성했다. 반면에 Node의 중심성(Centrality, $c_v$)은 Graph에 Node의 중요도까지 계산한 방식이다. 중심성을 계산하는 방식은 대표적으로 고유벡터 중심성(Eigenvector Centrality), 매개 중심성(Betweenness Centrality), 근접중심성(Closeness Centrality) 등이 있다. 고유벡터 중심성을 개선한 카츠 중심성, 페이지 랭크 등이 있으나 다루지 않는다. [참고]
Eigenvector Centrality
고유벡터 중심성은 중요한 Node들이 neighboring node로 되어 있다면, node $v$는 중요하다고 판단한다.
\[ c_v = \frac{1}{\lambda} \sum_{u \in N(v)} c_u \]
\[ \lambda \boldsymbol{c} = \boldsymbol{Ac} \]
이때 $\lambda$는 양수이며, $\boldsymbol{A}$는 인접 행렬(adjacency matrix), $\boldsymbol{c}$는 중심 벡터를 의미한다. $u$는 neighbor Node를 의미하고, $N(v)$는 $v$의 neighbor Node의 집합을 의미한다. 가장 큰 고유값 $\lambda_{max}$는 프로베니우스 정리에 의해 항상 양수이며 유일하다. 이에 대응되는 고유벡터 $\boldsymbol{c}_{max}$는 중심성을 판단하는데 사용된다.
Betweenness centrality
매개 중심성은 최단 거리의 path를 많이 가지고 있을수록 중요한 Node라고 판단한다. 예를 들어, A도시에서 C도시로 이동한다고 하자. 이동하는 과정에서 B도시를 무조건 거쳐서 가야된다고 한다면 B도시의 매개 중심성은 높게 측정된다.
\[ c_v = \sum_{s \neq v \neq t} \frac{ \text{shortest paths between s and t that contain v}}{ \text{shortest path length between u and v}} \]
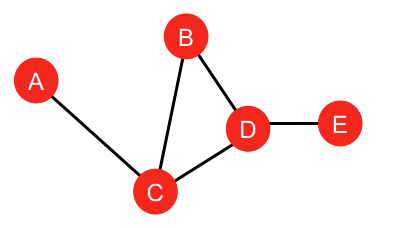
각 Node의 최단 경로를 생각하고, 이 때 Node가 속해 있다면 점수를 부여하는 형태가 된다. $C_A, C_B, C_E$의 경우는 0이 될 것이고, $C_C$의 경우는 A-C-B, A-C-D, A-C-D-E 에 속해 있기에 3을 부여한다.
Closeness centrality
근접 중심성은 중요한 노드일수록 다른 노드까지의 거리가 짧을 것이라는 가정에서 시작된다. 매개 중심성 수식에서 분자를 1로 변환하면 동일한 결과가 나온다.
\[ c_v = \frac{1}{\sum_{u \neq v} \text{shortest path length between u and v}} \]
위 그림을 예시로 들면, $C_A = \frac{1}{2 + 1 + 2 + 3} = \frac{1}{8} $, $C_D = \frac{1}{2 + 1 + 1 + 1} = \frac{1}{5} $가 된다.
Clustering Coefficient
Clustering Coefficient는 Node에 Neighbor Node가 얼마나 잘 연결되어 있는지 판단하는 지표며, 수식은 다음과 같다.
\[ e_v = \frac{\text{edges among neighboring nodes}}{ _{k_v}C_{2} } \]
clustering coefficient가 1인 경우는 모든 Neighbor Node가 연결되어 있다는 것을 의미하고, clustering coefficient가 0인 경우는 모든 Neighbor Node가 연결되어 있지 않다는 것을 의미한다.

Graphlets
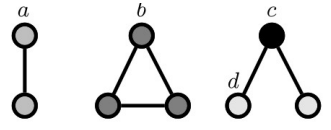
위 그림을 살펴보면 Edge들로 인해 생성되는 Triangle을 확인할 수 있다. $e_v =0.5$인 경우에는 아래의 그림과 같이 3개의 Subgraph인 Traingle을 생성한다. 이처럼 생긴 Subgraph는 Graphlets의 한 종류이다. Graphlets은 Graph에서 추출된 전부 이어져 있는 induced non-isomorphic subgraph를 의미한다.

induced subgraph는 임의의 노드를 선택했을 때 해당 노드들 사이에 연결된 모든 Edge들을 포함하는 subgraph를 의미한다. isomorphic graph는 그래프들 간의 Node가 같은 수를 가지고 있고, 두 그래프의 Node들이 똑같이 연결되어 있는 것을 의미한다. Graphlets은 non-isomorphic이기 때문에 똑같지 않은 subgraph들을 의미한다. 우리는 아래 그림에서 처럼 미리 지정된 Graphlets가 Graph 내에 얼마나 있는지 확인할 수 있다.

Graphlet Degree Vector (GDV)
GDV는 해당 노드에 대해 가능한 graphlet의 개수를 센 vector를 의미한다. 아래와 같은 Graph가 있다고 가정하자. 해당 Graph로 만들 수 있는 Graphlet은 2-node와 3-node Graphlet이 존재한다.

각 Node의 GDV를 계산하면 아래와 같다.

$c$의 경우는 왜 성립이 안되는지 의아할수도 있다. 위에서 우리는 Graphlet의 정의를 다시금 살펴볼 필요가 있다. Graphlet은 각 node가 전부 이어져 있는 edge를 포함한 subgraph를 의미한다. 따라서 node $v$를 $c$로 계산할 경우 일치하는 subgraph를 찾을 수 없다. 위 Graph의 경우 Node의 수가 총 5개이기 때문에 72개의 Coordinate Graphlets 중에서 2 부터 5개의 Node를 가진 $G_1$부터 $G_8$까지의 Graphlets을 고려하여야 한다. 이때 4개의 Graphlets에서 Connected가 있었기 때문에 4개의 Graphlets에 대해서만 Counting을 했다.
GDV는 노드의 Local Network topology의 지표를 제공한다. 두 Node의 Vector를 비교하는 것은 Node degree나 Clustering coefficient 보다 상세한 local topological similarity의 지표를 제공한다.
Summary
이번 Lecture에서는 Node-level에서 feature를 추출하는 방법에 대해서 소개했다. 중요도 기반으로 feature를 추출하는 방식인 Node Degree, Centrality measure와 Structure 기반으로 feature를 추출하는 Node degree, Clustering coefficient, Graphlet Degree Vector (GDV)에 대해서 알아보았다.
- Importance-based features
- Node degree: Simply counts the number of neighboring nodes
- Different node Centrality measures: eigenvector, betweenness, closeness centrality
- Structure-based features
- Node degree: Counts the number of neighboring nodes
- Clustering Coefficient: Measures how connected neighboring nodes are
- Graphlet Degree Vector: Counts the occurrences of different graphlets
'Deep Learning > CS224W' 카테고리의 다른 글
| [CS224W] Node Embeddings (0) | 2022.07.05 |
|---|---|
| [CS224W] Traditional feature-based methods: Graph-level features (0) | 2022.07.04 |
| [CS224W] Traditional feature-based methods: Link-level features (2) | 2022.07.03 |
| [CS224W] Choice of Graph Representation (0) | 2022.05.16 |
| [CS224W] Application of Graph ML (0) | 2022.05.16 |