[CS224W] Traditional feature-based methods: Link-level features

Contents

• Link Prediction Task and Features 
• Two formulations of the link prediction task
  • Links missing at random
  • Links over time
• Link-Level feature
  • Distance Based Features 
  • Local Neighborhood
    • Common neighbors 
    • Jaccard's coefficient
    • Adamic-Adar index
  • Global Neighborhood

 

이전 단계에서는 Node-Level prediction에 대한 내용을 다루었다. 이번 Lecture에서는 Link-Level prediction에 대해서 다룬다. Link는 Edge라고도 부르며 혼용해서 부르니 참고하길 바란다. 

 

Link Prediction Task and Features 

Linke-Level Prediction이란, 이미 존재하는 링크(Link)를 기반으로 노드 $A$와 노드 $B$ 간의 새로운 링크를 예측하는 것이다. 아래의 그림을 살펴보면 노드 $A$와 노드 $B$는 연결되어 있지 않지만, 연결될 가능성을 예측하는 등의 문제를 의미한다. 실제 테스트하는 단계에서는 모든 노드 쌍에 대해 순위가 매겨지고 top-K를 예측하는 형태로 진행된다. 이때 가장 핵심은 노드 쌍에 대한 특징(feature)을 설계(design)하는 것이다. 

 

 

Two formulations of the link prediction task

node-level prediction으로는 link-level prediction을 수행하는 것이 다소 어렵다. 그렇기 때문에 link-level prediction에서는 다음과 같은 두 가지 방식을 통해 링크를 예측한다. 

 

Links missing at random

무작위로 이미 연결되어 있는 링크를 지우고 그 링크를 예측하는 것에 초점을 두고 모델을 학습한다. 일반적으로 사용하는 방법이며, 머신러닝 알고리즘에서 사용하는 방법과 유사한 방법으로 진행하는 것이다. 이는, 생물학자들이 단백질 구조 간의 연결성을 파악하기 위한 연구에 많이 사용된다. 실제로 단백질 구조 간의 결합을 하지 않더라도 예측하는 것이 가능하기 때문이다. 

 

Links over time

시간이 지남에 따라 변화하는 그래프가 존재하는 경우 시점 $t_0$가 주어지고, 그래프 $G[t_0,t_0^{\prime }]$가 주어졌을 때 output은 다음 시점의 링크의 순위 리스트를 반환한다($G[t_1,t_1^{\prime }]$). 즉, 미래의 상태를 예측하는 것이다. 이를 evaluation하기 위해서는 n = $|E_{\text{new}}$가 주어졌을 때 다음 기간 $[t_1,t_1^{\prime }]$ 동안 관측된 새로운 link를 바탕으로 리스트 $L$ 내에 top-n개를 추출하고, 맞은 edge를 카운팅하는 방식으로 검증할 수 있다. 

 

Link-Level feature

그래프 내에서 두 노드 간의 관계에 대한 특징을 도출하는 방법은 Distance-base, Local neighborhood, Global neighborhood 총 3가지 방법이 존재한다. 각 방법이 어떠한 방식으로  특징을 도출하는지 확인해보자. 

 

Distance Based Features 

그래프의 구조를 보고 노드들에 대한 차수(Degree, $D$)를 구할 수 있다. $S_{BH},S_{BE},S_{AB}$는 각각 2개의 노드와 연결되어 있으므로 $D=2$가 되고, $S_{BG},S_{BF}$는 각각 3개의 노드와 연결되어 있으므로 $D=3$이 된다. 그러나 차수를 가지고 이들에 대한 정보를 제대로 포착하는 것은 상당히 어렵다. 

 

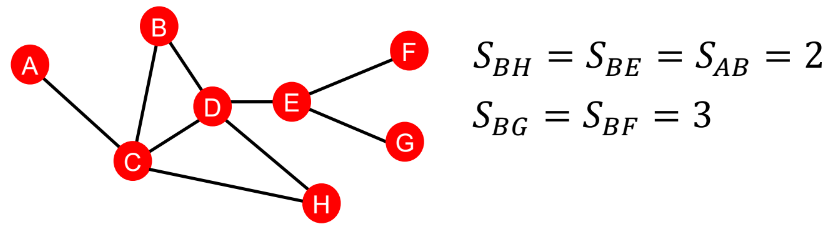
그렇다면 Distance 관점으로 바라보자. 노드 $B$에서 노드 $H$로 가는 링크 $(B,H)$는 $B\to C\to H$와 $B\to D\to H$ 총 2가지 길이 있다. 반면에, $(B,E),(A,B)$의 경우에는 각각 $B\to D$, $A\to C$ 하나의 길 밖에 존재하지 않는다. 이런 정보를 바탕으로 feature를 추출하는 것이 바로 Distance-Based Feature이다. 

 

 

Local Neighborhood

Local Neighborhood는 노드 $A$와 노드 $B$간 얼마나 이웃을 많이 공유하는가를 기반으로 link를 예측하는 방법이다. 가장 간단한 방법으로는 Common neighbors가 있으며, Jaccard's coefficient, Adamic-Adar index 등의 방법이 존재한다.

 

Common neighbors 

Common neighbors는 가장 간단한 방법이며, 단순히 노드 $A$와 노드 $B$의 이웃이 얼마나 많이 겹치는지를 나타내는 지표다. 노드 $A$와 노드 $B$에 대한 집합을 각각 $N(A)$, $N(B)$로 표현하면 겹치는 이웃은 $|N(A)\cap N(B)|$로 표현할 수 있다. 아래의 경우를 예로들면 $N(A)=C$, $N(B)=C,D$로 $|N(A)\cap N(B)|=|C|=1$이 되는 것이다.

 

 

Jaccard's coefficient

Jaccard's coefficient는 자연어처리를 다루는 사람에게는 익숙한 지표일 수 있다. 먼저 Common neighbor으로 구한 각 이웃 간의 교집합을 합집합으로 나눈 것으로 비율을 나타낸다고 이해할 수 있다. Common neighbor의 경우에는 단순히 정수의 표현으로 나타나기 때문에 노드에 대한 이웃이 많다면 값이 커져서 파악하는 것이 어려울 수 있으나, Jaccard's coefficient 경우에는 비율로 나타나기 때문에 의미를 보다 잘 이해할 수 있다. 본 강의에서는 common neighbor의 normalized version을 jaccard's coefficient라고 언급한다. 

$$\frac{|N(A)\cup N(B)|}{|N(A)\cup N(B)|}$$

 

Adamic-Adar index

Adamic-Adar index는 노드 $A$와 노드 $B$의 공통된 이웃에 대해서 그 이웃들의 차수에 로그를 씌우고 역수를 취해 더하는 값을 의미한다. 

$$\sum _{u\in N(A)\cap N(B)}\frac{1}{\log (k_u)}$$

이때 $k$는 이웃 노드의 차수를 의미한다. 이는 이웃 노드의 중요도를 고려한 것이다. 만약 이웃 노드가 다른 노드에 대해서 모두 연결되어 있디면 Adamic-Adar index의 값은 낮은 값을 띈다. 반면에, 노드 $C$가 노드 $A,B$만 연결되어 있다면 Adamic-Adar index는 높은 값을 띈다. 이는 연결된 노드의 중요도까지 고려한 것으로 볼 수 있다. 예를 들어, 소셜 네트워크에서 C라는 친구가 A와 B만 팔로우를 하고 있다면 A와 B도 서로 알 수 있는 친구라고 예측하는 것이다. 

 

 

Global Neighborhood

Global Neighborhood는 Local Neighborhood의 한계점을 극복하기 위해 제안된 방법이다. 만약 노드 $A$와 노드 $B$ 간의 공통된 이웃이 없는 경우에는 두 노드의 이웃 간의 교집합은 공집합($\varphi$)이 된다. 즉, 0을 의미한다. 두 노드 간에는 미래에 잠재적으로 연결될 가능성이 있을 수 있으나 Local Neighborhood를 통해 Link를 예측하는 경우 이를 반영할 수 없다. Global Neighborhood는 이를 극복하기 위해 Katz index를 사용한다. Katz index는 그래프의 중심성을 다룰 때 본 적이 있을 수 있다. 중심성이 0이 나오는 경우 이를 통해 해결할 수 있는데, 여기서 언급하는 방법도 마찬가지이다. 

 

Katz index는 인접 행렬(Adjacency Matrix)를 통해 모든 노드쌍의 경로(path)의 수를 모든 길이에 대해서 count하는 방식이다. 이때 길이가 1인 경우가 인접행렬이고, 2인 경우는 다음과 같이 표현할 수 있다.

$$\begin{array}{rl}{P}_{uv}^{(1)}& =A_{uv}\\ P_{uv}^{(2)}& =\sum _i{A}_{ui}\ast P_{iv}^{(1)}=\sum _i{A}_{ui}\ast A_{iv}=A_{uv}^2\end{array}$$

길이가 2인 경우에는 노드 $u$에서 노드 $v$로 가는 경우 중간 노드가 하나 존재하는 것을 의미한다. 이 경우 아래와 같이 행렬 곱으로 표현할 수 있다. 

 

 

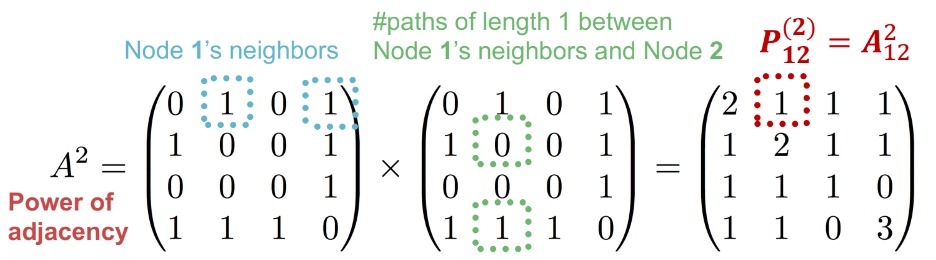
Katz index는 이렇게 계산된 모든 길이에 대한 인접행렬에 $\beta$를 곱하여 합산한 값을 의미한다. $\beta$는 0과 1사이의 값을 가지며 discount factor를 의미한다. 닫힌 구간에서 katz index의 행렬 form은 다음과 같다. 

$$\begin{array}{rl}{S}_{v1,v2}& =\sum _{l=1}^{\mathrm{\infty }}{\beta }^l{\mathit{A}}_{v1,v2}^l\\ S& =\sum _{i=1}^{\mathrm{\infty }}{\beta }^i{A}^i=(\mathit{I}-\beta \mathit{A}{)}^{-1}-\mathit{I}\end{array}$$

갑자기 $(\mathit{I}-{\mathit{A}}^{-1})$이 나와서 당황할 수 있으나 이는 행렬의 기하급수, 등비수열을 이용하면 쉽게 증명이 가능하다. 자세한 내용은 여기를 참고하길 바란다.

 

 

Summary

Distance-based features는 두 노드 간의 가장 짧은 경로를 사용하였으나, 노드 간의 이웃들이 겹치는 것에 대한 정보는 포착하지 못한다. Local neighborhood overlap은 노드들 간의 이웃들이 겹치는 정도를 파악할 수 있으나, 겹치는 이웃이 없는 경우에는 계산하는 것이 불가능하다. 마지막으로 Global neighborhood overlap의 경우에는 katz index를 사용하여 두 노드의 모든 길이에 대해서 계산하기 때문에 노드 간의 이웃이 겹치지 않더라도 이를 파악하는 것이 가능하다.