Contents
본 강의는 Lecture 3.1로 Node Embedding에 대해서 다룬다. 일단 먼저 Embedding이라는 단어가 무엇인지 알고 있어야 한다. 자연어처리(NLP)에서는 단어를 One-hot Encoding으로 혹은 Look-up Table로 만든 후 Embedding을 진행한다. Embedding은 아무런 의미가 없는 데이터를 임의의 차원으로 보냄으로써 그 숫자 자체에 의미를 지닐 수 있도록 하는 개념으로 이해할 수 있다. Node Embedding도 비슷한 맥락으로 Embedding 값이 가지는 수치를 통해 Node의 특징(feature)을 파악할 수 있도록 하는 것이다. 본 강의에서는 Node Embedding을 하는 방법을 총 4가지 단계로 나누어서 언급한다.
1. Encoder maps from nodes to embeddings
2. Define a node similarity function
3. Decoder $\text{DEC}$ maps from embeddings to the similarity score
4. Optimize the parameters of the encoder
위 과정에 따라 작성할 예정이며, 일단 먼저 진행하기에 앞서 Node Embedding이 무엇을 의미하는지 개념부터 알아보자.
Node Embedding
전통적인 머신러닝 기법을 통해 그래프를 학습하기 위해서는 feature engineering을 사용하여 node-level, edge-level, graph-level 등의 feature를 추출하고 이를 학습한 후 예측하는 형태로 진행한다. 그러나 feature engineering은 사람이 직접 처리를 해주어야 한다는 어려움이 존재해, 최근에는 자동으로 feature를 추출하는 Representation Learning을 사용한다. Representation Learning은 각각의 노드를 하나의 feature representation, 즉 feature vector로 변환하는 것이다.

노드에 정보가 주어졌을 때 이를 d 차원의 공간으로 할당하여 feature vector를 생성하게 된다. 이렇게 생성된 embedding 값은 Node classification, Link prediction, Graph classification 등 다양한 분야에 적용하는 것이 가능하다.
Encoder
Node Embedding을 진행할 때 Encoder와 Decoder를 구축하여야 하는데, 먼저 Encoder를 어떤 식으로 구축하는지 알아보자. 우리는 그래프가 주어지면 인접행렬(adjacency matrix)을 만들 수 있다. 그러나 인접행렬만을 가지고는 그래프 노드의 feature를 제대로 추출할 수 없다. 따라서, 원래 그래프를 Encoding하여 embedding space로 mapping시키는 encode 함수 $\text{ENC}$를 구축하여야 한다.
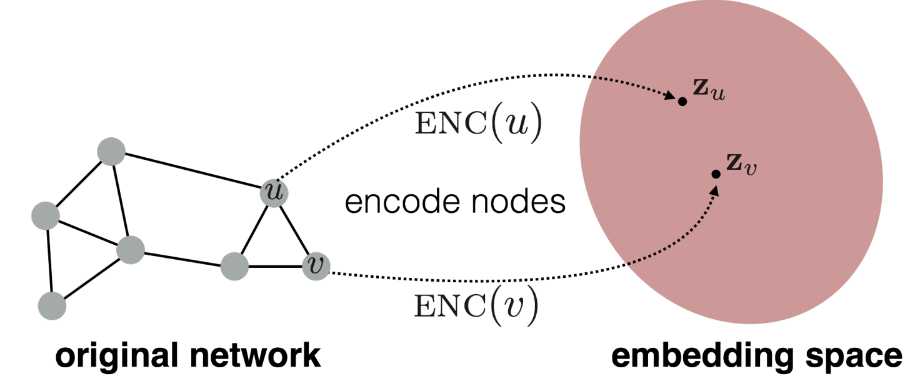
embedding space에서는 각 노드들의 feature vector가 orthogonal 하지 않기 때문에 내적을 할 수 있으므로, 노드 간의 유사성을 계산하는 것도 가능하다. 노드들을 embedding space에 제대로 할당하기 위해 encoding 함수를 제대로 학습하여야 한다.
\[ \text{ENC}(v) = z_v = Z \cdot v \]
이때 $v$는 입력으로 들어온 그래프를 의미하고 $z_v$는 d차원의 embedding 값을 의미한다. $v \in \mathbb{I}^{|V|}$는 indicator vector로 One-hot encoding과 동일한 개념으로 볼 수 있다. $Z \in \mathbb{R}^{d \times |V|}$는 weight matrix를 의미하며, 이를 학습하는 것이 목표다.

각각의 노드들은 고유한 embedding vector를 할당받으며, Node Embedding을 수행하는 방법은 다양한 방법들이 존재한다. 대표적인 기법으로는 DeepWalk, Node2Vec 등이 있다.
DeepWalk
DeepWalk는 2014년 KDD에 발표된 논문으로 Node Embedding이라는 개념을 언급한 논문이다. Karate Club 이라는 유명한 Graph 구조 데이터셋이 있는데, 이를 입력으로 넣었을 때 오른쪽 그림과 같이 2차원 공간에 mapping할 수 있다. 그림을 살펴보면 노드의 색깔끼리 군집화되어 있는 것을 확인할 수 있다. 본 논문은 Word2Vec의 방식을 사용하여 Word대신 Node를, 문장 관계 대신 Walk를 사용하였다.

지금까지 다룬 Encoding 방법은 매우 얕은(shallow) 방법이다. 즉, 매우 간단한 방법으로 노드를 Embedding한 것이다. 다음 강의에서는 GNN을 활용한 deep encoder에 대해서 다룬다.
Decoder
Decoder는 Encoder에 비해 간단하다. Encoder를 통해 embedding space에 mapping된 데이터들이 원래의 그래프에서의 관계에 매핑되는 방법을 지정하는 역할을 한다.
\[ \text{Goal}: \text{similarity}(u,v) \approx z^T_vz_u \]
$z^T_v z_u$는 내적을 의미하며, $\text{similarity}$는 원래 그래프에서 노드 $u$와 노드 $v$ 간의 유사도를 의미한다. 이때 두 노드의 내적의 값을 최대화 하는 방식으로 학습을 진행한다. 그렇다면 우리는 내적을 통해 계산한 유사도를 정의할 수 있어야 한다. 두 노드가 연결되어 있을 때 유사하다고 판단할 것인가? 아니면 이웃을 공유하는 경우? 구조적인 역할이 유사할때?
본 강의에서는 Random walks 방식을 사용하여 노드의 유사성을 정의하는 것과 유사도를 측정을 위해 Embedding을 어떻게 최적화 할 수 있는지를 다룬다. random walk 방식은 unsupervised 혹은 self-supervised 방식을 통해 노드 Embedding을 학습한다. 학습하는 과정에서 노드의 label과 feature를 사용하지 않기 때문이다.
Random Walk Approaches for Node Embedding
앞에서는 가장 간단한 node embedding 방법인 'shallow' embedding 방법에 대해서 다루어보았다. 이번에는 Random Walk를 이용한 방법론에 대해서 다루어보자. 앞에서 언급한 DeepWalk가 Ramdom Walk 방식과 관련있다. 계량경제학이나 주식에 관심 있는 사람이라면 Random Walk라는 단어들 들어본 적 있을 것이다. 말 그대로 무작위로 이동하는 것을 의미한다. 시작 노드로부터 무작위로 움직이면서 다음 도착할 노드에 대한 확률값을 도출하는 것이다.

웃고 있는 노드(starting node)를 기준으로 노드 1, 노드 3, 노드 5 중 아무 노드로 움직이면서 진행한다. 위 경우에는 노드 5인로 이동한 경우를 나타내고 있다. 첫 번째 단계를 거쳐 노드 5로 이동하게 되면 노드 5는 시작 노드, 노드 6, 7, 8로 이동할 수 있다. 이와 같은 방식으로 시작 노드 $\rightarrow$ 노드 5 $\rightarrow$ 노드 8 $\rightarrow$ 노드 9 $\rightarrow$노드 8 을 거쳐 최종적으로 노드 11에 도착한다.
random Walk에서는 위와 같은 방식으로 엣지를 통해 노드를 이동하면서 노드 u와 노드 v 간의 동시에 발생할 확률을 추정한다. 조금 더 구체적으로 말하자면, 시작 노드 u에서 random Walk Strategy $R$을 사용하여 최종 노드가 v일 확률을 예측하는 것이다.

위에서 도출된 조건부 확률 $P_R(v|u)$를 encoding 하기 위해 embedding을 최적화 한다. 최적화된 embedding을 통해 각 노드에 대한 prepresentation을 내적(dot product)하여 유사도를 계산한다. 즉, $z^T_u z_v$를 계산하는 것이다. 이와 같은 방식은 다음과 같은 장점이 존재한다.
1. Expressivity
Random Walk를 통한 node similarity는 Local 이웃 정보와 higher-order 이웃 정보를 통합하는 확률적 정의이기 때문에 매우 표현력이 좋다. 시작 노드 u에서 높은 확률로 노드 v에 도달한다면, 노드 u와 노드 v가 유사하다고 판단하며, 이는 high-order multi-hop information을 의미한다.
2. Efficiency
Random Walk에서는 오직 동시 발생한(예를 들면, 노드 u와 노드 v만) pair에 대해서만 고려하기 때문에, 모델을 학습할 때 모든 노드에 대한 pair를 고려할 필요가 없어서 매우 효율적이다.
Unsupervised Feature Learning
Random Walk 방식은 기본적으로 Unsupervised Learning으로 분류된다. 그렇다면 먼저 Unsupervised Learning이 어떤 것인지 알고 넘어가야 한다. Unsupervised Learning은 유사도를 보존할 수 있는 d-차원의 공간에서의 node embedding을 찾는 것이다. 네트워크 구조에서 서로 가까운 노드가 서로 가깝게 위치하도록 노드 임베딩을 학습하는 방식으로 진행된다.
Random Walk Optimization
그렇다면, 노드 u가 주어졌을 때 가까운 노드라는 것을 어떻게 정의할 수 있을까? Random Walk strategy $R$로 구한 노드 u의 이웃 집합 $N_R(u)$가 있다고 하자. 그렇다면 Log-likelihood 를 사용하여 노드 u가 주어졌을 때 $N_R(u)$와의 조건부 확률 값이 최대가 되는 방향으로 학습하여 노드 u의 feature representation을 도출할 수 있다.
\[ \underset{f}{\text{max}} \sum_{u \in V} \log P(N_R(u)|\boldsymbol{z}_u) \]
이때 $f: u \rightarrow \mathbb{R}^d: f(u) = \boldsymbol{z}_u$를 의미하며, 노드 u의 embedding을 나타낸다. 이를 최적화하여 적절한 feature representation을 찾는 것이 목적이다.
Random Walk를 통한 최적화 방식은 총 3 단계를 거친다. 먼저, 고정된 길이의 rnadom walk를 실행하고, 시작 노드 u로 부터 random walk strategy $R$을 사용한다. 두 번째로는, 각각의 노드에 대해서 $N_R(u)$를 산출한다. 이때 $N_R(u)$, 즉, 노드의 이웃 집합은 시작 노드 u에서 마지막 방문한 노드들의 집합을 의미한다. 마지막으로는, 그래프 내에 있는 모든 노드들에 대해서 노드 u가 주어졌을 때 $N_R(u)$가 나타날 조건부 확률을 최대화하는 방향으로 최적화한다. 즉, 위에서 언급한 목적함수를 최적화하며, 다음과 같은 형태로도 사용할 수 있다.
\[ \mathcal{L} = \sum_{u \in V} \sum_{v \in N_R(u)} - \log ( P (v|\boldsymbol{z}_u)) \]
MLE를 최대화하는 방식은 Cross Entropy를 최소화하는 방식으로 변환할 수 있기 때문이다. 우리는 이처럼 likelihood를 최대화하는 방식으로 embedding $z_u$를 최적화한다. 이때 조건부 확률 $P(v|\boldsymbol{z}_u)$를 정의해야 최적화할 수 있을 것이다. 이때, softmax 함수를 사용하여 다음과 같이 매개변수화 할 수 있다.
\[ P(v|\boldsymbol{z}_u) = \frac{\exp(\boldsymbol{z}^T_u \boldsymbol{z}_v)}{\sum_{n \in V} \exp(\boldsymbol{z}^T_u \boldsymbol{z}_n)} \]
softmax 함수를 사용하여 조건부 확률을 매개변수화 하는 이유는 다음과 같다. 우리는 모든 노드에 대해서 노드 u와 가장 유사한 node v를 찾고자 한다. 위 수식을 살펴보면 모든 노드에 대해서 $\exp(\boldsymbol{z}^T_u \boldsymbol{z}_v)$ 즉, 유사도가 가장 높은 노드 v를 찾는 수식과 동일하다. 직관적으로 $\sum_i \exp(x_i) \approx \underset{i}{\max} \exp(x_i)$ 이기 때문이다. 이제 위 수식을 종합하여 다음과 같은 수식으로 정리할 수 있다.
\[ \mathcal{L} = \sum_{u \in V} \sum_{v \in N_R(u)} -\log ( \frac{\exp(\boldsymbol{z}^T_u \boldsymbol{z}_v) }{\sum_{n \in V} \exp(\boldsymbol{z}^T_u \boldsymbol{z}_n)}) \]
가장 앞에 있는 수식인 $\sum_{u \in V}$는 모든 노드 u에 대한 합을 의미하고, $\sum_{v \in N_R(u)}$은 시작 노드 u에서 random walk를 통해 관찰되는 노드 v의 합을 의미한다. 마지막으로, $\frac{\exp(\boldsymbol{z}^T_u \boldsymbol{z}_v)}{\sum_{n \in V} \exp (\boldsymbol{z}^T_u \boldsymbol{z}_n)} $는 random walk에서 노드 u와 노드 v가 같이 관찰될 확률을 예측하는 것을 의미한다.
Negative Sampling
그러나 위 수식은 전체 노드 수의 제곱에 비례하는 시간 복잡도 $O(|V|^2)$을 가진다. 즉, 계산 비용이 매우 비싸다. 따라서, 본 논문에서는 Negative Sampling을 통해 시간 복잡도를 줄였다. 모든 노드에 대해 normalizing 하는 것이 아니라, k 개의 노드에 대해서만 계산을 하는 것이다. 이를 수식으로 표현하면 다음과 같다.
\[ \log( \frac{\exp(\boldsymbol{z}^T_u \boldsymbol{z}_v) }{\sum_{n \in V} \exp ( \boldsymbol{z}^T_u \boldsymbol{z}_n)}) \approx \log(\sigma (\boldsymbol{z}^T_u \boldsymbol{z}_v ) ) - \sum^k_{i=1} \log (\sigma ( \boldsymbol{z}^T_u \boldsymbol{z}_{n_i})), n_i \sim P_V \]
$\sigma$는 sigmoid 함수를 의미하고, $n_i$는 negative sample을 의미하며, $n_i \sim P_V$는 uniform random distribution으로 negative sample을 선정하는 함수다. Negative sampling 개념은 Word2Vec에서 나오니 논문을 참고하길 바란다. 이때 negative sample의 수를 나타내는 k가 클수록 robust estimate를 도출할 수 있다. 그러나 k가 커질수록 negative sample로 인해 높은 bias가 발생할 수 있기 때문에 일반적으로 5에서 20사이의 negative sample을 선택한다.
그래프 내에 노드가 10만 개가 존재하는 경우 negative sampling을 사용하면 5개 혹은 20개 사이의 노드에 대해서만 계산을 하면 되지만, negative sampling을 사용하지 않는다면 모든 노드 즉, 10만 개의 노드에 대해 계산을 진행해야 하기 때문에 엄청나게 시간이 많이 소요된다.
Stochastic Gradient Descent
이번에는 위 함수를 최적화하는 방법에 대해서 다루어보자. 최적화하는 방법에는 SGD, Adam, RMSProp 등 다양한 방법이 존재하지만 본 강의에서는 SGD에 대해서만 다룬다. SGD에 앞서 GD(Gradient Descent)에 대해서 먼저 다루어보자. GD는 목적 함수를 최적화하는 가장 간단한 방법 중 하나이다. 먼저, 모든 노드에 대해서 임의의 초기 값 $z_i$를 설정한다. 그 후 각각의 노드 i에 대해서 편미분 값을 구하고, 도출된 결과에 learning rate를 곱해 초기 $z_i$를 수정한다.
\[ z_i \leftarrow z_i - \eta \frac{\partial \mathcal{L}}{\partial z_i} \]
SGD는 GD와는 다르게 Stochastic이 추가되었다. 모든 노드에 대해서 한번에 기울기를 계산하여 노드의 representation을 수정하는 것이 아니라, 각각 개별적인 노드에 대해서 하나하나씩 최적화하는 방식이다.
\[ \begin{equation} \begin{split} \mathcal{L}^{(u)} & = \sum_{v \in N_R(u)} - \log (P(v|\boldsymbol{z}_u)) \\ z_j & \leftarrow z_j - \eta \frac{\partial \mathcal{L}^{(i)}}{\partial z_j} \end{split} \end{equation} \]
GD와 SGD는 각각의 장단점이 존재한다. 이와 관련된 내용은 여기를 참고하길 바란다.
Summary
1. 그래프 내 각각의 시작 노드에 대해서 random walk를 실행한다.
2. 각 노드에 대한 이웃 집합 $N_R(u)$를 구한다.
3. 이때 목적함수는 negative sampling과 Cross Entropy를 사용하여 목적함수를 SGD를 통해 최적화한다.
위 내용을 통해 어떻게 random walk 전약을 짤 수 있을까라는 의문이 생길 수 있다. 가장 간단한 아이디어는 위에서 다룬 논문인 DeepWalk에서 제안하였다. DeepWalk에서는 고정된 길이에 대해서만 unbiased하게 random walk를 수행하는 방법을 제안하였다. 그러나 이와 같은 방식은 유사성의 개념이 너무 제한적이라는 문제가 존재한다. 이를 해결하기 위해 나온 기법이 바로 Node2Vec이다.
Node2Vec
Node2Vec의 목표는 feature space에서 유사도를 보존할 수 있는 노드 embedding을 찾는 것이다. 이 목표를 목적함수를 최대화하는 문제와 downstream에서의 prediction task로 frame화 할 수 있다. 이때 가장 중요한 것은 네트워크에서 노드 u의 이웃의 개념이 각 node embedding에 유연하게 이어져야 한다. 다시 말해, 실제 관계를 feature space에서도 잘 표현하여야 한다는 것이다.
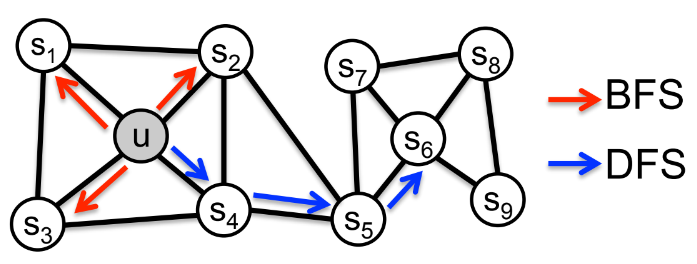
본 논문에서는 biased Random Walk를 유연하게 사용한다. 이는 Local view와 global view의 균형을 맞출 수 있다. 이때 주어진 노드 u의 이웃 노드 집합을 찾는 전략으로 BFS(Breadth-First Search)와 DFS(Depth-First Search)를 사용한다. BFS는 너비를 우선적으로 탐색하는 방법으로 위 그림의 경우 먼저 길이가 1인 노드를 먼저 파악함으로써 Local view를 볼 수 있다. 반면제, DFS는 깊이를 우선적으로 탐색하는 방법으로 현재의 노드에서 갈 수 있는 점들까지 전부 살펴봄으로써 Global view를 볼 수 있다.
Biased fixed-length random walk $R$에서는 파라미터 $p$, $q$를 사용하며 다음과 같이 정의한다.
$p$: 이전 노드로 돌아갈 가능성.
$q$: DFS와 BFS의 비율.
노드 u에서 길이가 2인 경우를 예시로 들어보자.



시작노드는 u하여 노드 W에 도달하였다. 이 때 W에서 random walk는 어디로 움직여야 할지 결정해야 되며, $s_1, s_2, s_3$으로 갈 수 있다. $s_2$로 갈 경우 이전 노드 $s_1$에서 W 까지의 거리와 노드 $s_2$까지의 거리가 동일하기 때문에 1로 표기한다. 반면에, $s_1$로 움직일 경우 이전 노드로 돌아갈 가능성을 나타내는 값의 역수인 $\frac{1}{p}$로 표기하고, 더 멀어지는 경우인 $s_3$은 $\frac{1}{q}$로 표기한다. 이처럼 W에서 각각의 노드에 대한 확률을 구하고, 이전 노드 $s_1$과의 거리를 계산하면 마지막 그림과 같은 결과를 도출할 수 있다. 이때 $\frac{1}{p}$와 $\frac{1}{q}$는 정규화하지 않은 가능성을 의미한다.
Summary
Node2Vec는 총 3가지 단계로 요약할 수 있다. 먼저, random walk의 확률을 계산한다. 두 번째로는, 각각의 노드 u에 대해서 l 길이의 random walk를 시뮬레이션한다. 마지마긍로, SGD를 통해 Node2Vec의 목적함수를 최적화한다. 이는 Linear-time 복잡도를 가지기 때문에 기존 방식에 비해 매우 효율적이다. 또한 3가지 단계를 개별적으로 병렬처리가 가능하다.
지금까지 Random Walk 방식 중에서 DeepWalk와 Node2Vec에 대해서 다루어 보았다. 두 방식 이외에도 다음과 같은 다양한 방식의 Random Walk가 존재한다.
Different kinds of biased random walks:
metapath2vec: Scalable Representation Learning for Heterogeneous Networks [Link]
Watch Your Step: Learning Node Embedding via Graph Attention [Link]
Alternative optimization schemes:
LINE: Large-scale Information Network Embedding [Link]
Network preprocessing techniques:
HARP: Hierarchical Representation Learning for Networks [Link]
struc2vec: Learning Node Representations from Structural Identity [Link]
본 강의에서 다룬 방법들은 각각의 장단점이 존재한다. 해당 논문은 각각의 task를 다룰 때 우수한 성능을 발휘하는 모델에 대한 정리를 해두었다.
'Deep Learning > CS224W' 카테고리의 다른 글
| [CS224W] PageRank (0) | 2022.07.18 |
|---|---|
| [CS224W] Embedding Entire Graphs (0) | 2022.07.13 |
| [CS224W] Traditional feature-based methods: Graph-level features (0) | 2022.07.04 |
| [CS224W] Traditional feature-based methods: Link-level features (2) | 2022.07.03 |
| [CS224W] Traditional feature-based methods: Node-level features (0) | 2022.05.17 |