Contents
Lecture 4 에서는 그래프 분석과 학습하는 방식을 행렬 관점으로 접근한다. 이번 글에서는 그 중 PageRank에 대해서 먼저 알아볼 것이며, PageRank는 이전 강의에서 다룬 Random Walk 방식을 사용하여 node의 중요도를 파악하는 방식이다.
PageRank
PageRank는 Stanford 대학의 박사 두 분이 만든 모델이다. PageRank에서의 Node는 web page를 의미하고, Edge는 hyperlinks를 의미한다. web에 방문하여 hyperlink를 클릭해 다른 web page로 이동하는 경우를 그래프로 표현한 것이며, 방향성을 가지는 directed graph를 뜻한다.


논문에서 citation을 달아 놓은 경우 논문에서 link를 클릭해 다른 논문으로 넘어가는 경우가 있을 수 있으며, Wiki나 Encyclopedia와 같은 문서에서 필요한 정보를 찾기 위해 link를 클릭해 넘어가는 경우도 있을 것이다. 본 강의에서는 Wikipedia와 유사한 Encyclopedia를 예시로 PageRank를 설명한다.
노드의 중요도를 파악하기 위한 방법은 다양하지만, 본 강의에서는 노드의 중요도를 계산하기 위해 아래와 같은 접근 방식(Link approaches)을 사용한다.
- PageRank
- Personalized PageRank (PPR)
- Random Walk with Restart
Link approaches는 page에 많은 in-link가 존재하는 경우, 중요한 page라는 아이디어를 전제로 한다. in-link가 많은 page의 경우 중요한 정보를 담고 있는 것을 의미할 수 있으며, page의 in-link가 거의 없다면 별다른 중요도가 없는 것으로 판단할 수 있기 때문이다. 논문의 경우 in-link는 인용 수를 의미하며 영향력 있는 논문일수록 인용 수가 높다. 반면에, 영향력이 없거나 논문의 질이 낮을 수록 해당 논문을 인용하는 사람은 거의 없을 것이다. 이와 같은 맥락으로 이해할 수 있다.
PageRank도 위에서 언급한 기본적인 가정을 따르고 있다. 아래의 그림에서 node j의 중요도를 구하기 위해서는 in-link를 살펴보아야 한다. $r$은 노드의 중요도를 의미하며, 각 노드의 중요도를 해당 노드의 out-link의 수 만큼으로 나누어 준 것이 in-link의 값이다. node j를 예로 들면, node j의 in-link는 node i와 node j로 구성되어 있으며, 각각의 중요도 $r_i/3$, $r_k/4$을 더한 것이 바로 node j 의 중요도 $r_j$가 되며, 수식을 일반화하면 다음과 같다.
\[ r_j = \frac{r_i}{d_i} + \frac{r_k}{d_k} = \sum_{i \rightarrow j} \frac{r_i}{d_i} \]

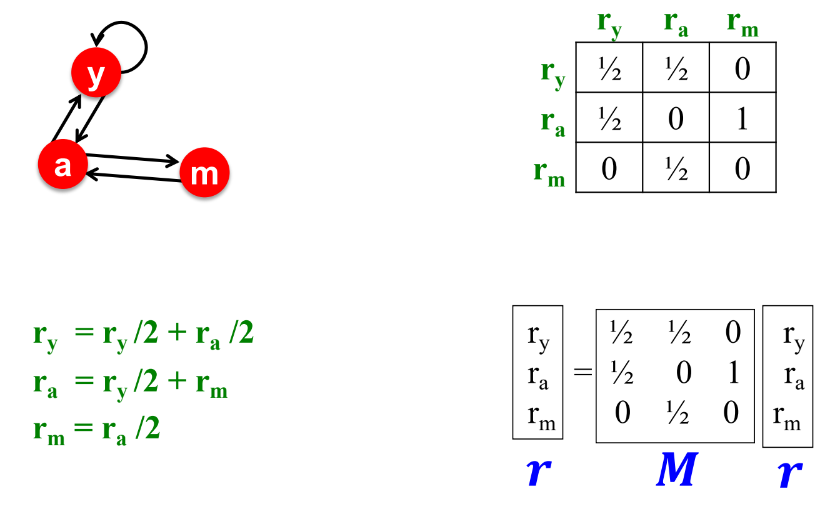
$d_i$와 $d_k$는 각 node out-link의 차수를 의미한다. 이와 같은 방식은 node의 수가 많아질수록 계산하는 것이 어렵기 때문에 matrix formulation으로 변환하여 사용할 수 있다. matrix formulation으로 변환하기 위해서 Stochastic adjacency matrix를 사용하며, Stochastic adjacency matrix는 $j \rightarrow i$일 때, $M_{ij} = 1/d_j$로 구성된다. $M$은 column stochastic matrix라고도 부르며, column은 각 node의 in-link를 의미하며, column의 합은 1이 된다.

이때의 Rank vector $r_i$은 $\sum_i r_i = 1$로 정의할 수 있으며, 위에서 다룬 수식을 matrix formulation 으로 변환하면 아래와 같은 수식을 도출할 수 있다.
\[ r = M \cdot r, \ \ r_j = \sum_{i \rightarrow j}\frac{r_i}{d_i} \]
web surfer가 random walk로 움직이는 것을 생각할 때 t+1 시점의 surfer는 probability distribution $p(t)$에 의해 결정될 것이다. 이 분포를 기반으로 다음 시점 t+1의 surfer의 위치에 대한 확률을 도출할 수 있으며 이때 아래의 수식이 성립하면 $p(t)$는 random walk의 stationary distribution을 의미한다.
\[ p(t+1) = M \cdot p(t) = p(t) \]
그렇다면, $r = M \cdot r$에서의 $r$ 역시 random walk를 위한 stationary distribution으로 이해할 수 있다. 이때의 좌항의 $r$은 이후 시점의 각 node들에 대한 rank vector(probability distribution)를 나타내고, 우항의 $r$은 이전 시점의 각 node들에 대한 rank vector(probability distribution)를 나타내기 때문이다.
선형대수에서 eigen value와 eigen vector는 $\lambda c = Ac$로 표현할 수 있다. 이때 $\lambda$는 eigen value, $c$는 eigen vector를 의미하고 $A$는 adjacency matrix를 의미하는데 $r = M \cdot r$과 매우 유사한 꼴을 지니고 있다. eigen value가 1인 경우를 생각하면 $ 1 \cdot r = M \cdot r$로 eigen value =1, eigen vector = $r$이 된다. 그러나 이처럼 eigen vector를 통한 node의 중요도 파악은 아주 특수한 경우에 중요도가 0이 나올 수 있다. 이런 경우를 개선한 중요도 방식이 kat'z 있으며, 자세한 내용은 여기를 참고하면 된다.
How to Solve?
그렇다면 $r$을 어떻게 최적화할 수 있을까? 최적화를 하기 위해서는 목적함수(Object Function)가 필요하다. 따라서, PageRank에서는 목적함수를 다음과 같이 정의한다.
\[ \sum_i |r^{t+1}_i - r^t_i | < \epsilon \]
즉, t 시점의 $r^t$과 t+1 시점의 $r^{t+1}$ 간의 차이를 최소화하는 형태로 $r$을 최적화하는 것이다. 학습하기에 앞서 먼저 $r$의 초기치를 설정해주어야 한다. 그 후 오차가 $\epsilon$이 될 때까지 반복 수행한다.
- Initialize: $r^0 = [ 1/N,..., 1/N]^T $
- iterate: $r^{t+1} = M \cdot r^t $
- Stop when $|r^{t+1}-r^t|_1 < \epsilon $
이때 $|x|_1$은 $L_1$ normalization을 의미한다. $L_1$ 뿐만 아니라 Euclidean을 사용해도 무방하다($L_2$ norm). 위 과정을 50번 정도 반복하게 되면 $r$이 수렴하는데, 구글의 경우 이 과정을 매일매일 반복해야 되기 때문에 엄청나게 많은 양의 연산이 요구된다. 또한, 위와 같은 방식으로 수행하는 경우 Dead ends와 Spider Trap에 직면할 수 있다. 이는 PageRank에서 $r$이 수렴하지 못하도록 방해하는 요인들이며, 각각이 어떤 내용인지 알아보자.
Dead ends
Dead ends는 해당 Page에서 더이상 빠져나갈 Hyperlink가 존재하지 않는 것을 의미한다. 즉, out-link가 없는 것이다.

위 구조를 Dead ends라 부른다. $r_a, r_b$가 처음에는 [1,0]의 값을 가지지만, 한 번 반복한 경우 [0,1]이 되며 그 후부터는 link가 존재하지 않아서 [0, 0]을 가지게 된다. 더이상 나갈 곳이 없기 때문에 중요도가 사라지는 것이다.
solution
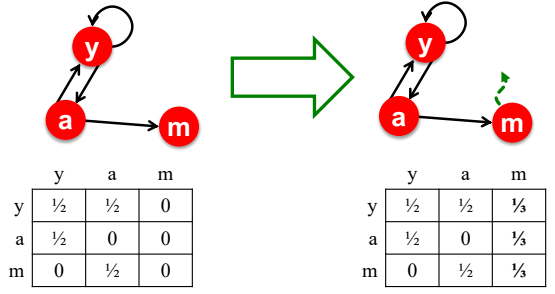
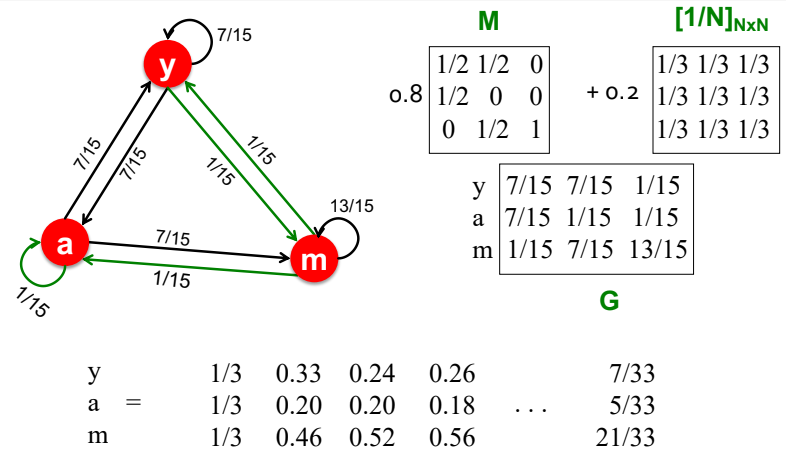
Dead ends에서 빠져나오기 위해서는 dead end에서 다른 node로 이동할 확률을 균등하게 분배해 무작위로 teleport하는 것이다. 원래의 node m에서는 out-link가 없기 때문에 column의 합이 0이지만, node y, a, m에 각각 균등하게 1/3의 값을 부여해 teleport할 확률을 부여한다. 이와 같은 방식을 통해 Dead end에서 빠져나올 수 있다.
Spider Traps
Spider Trap은 Dead end와는 다르지만, 밖으로 나가는 out-link가 없는 Page들의 집합을 의미한다. Web에서 어떤 Page로 들어왔을 때 그 Page들만 순회하는 즉, Cycle 구조를 가지고 있는 형태를 의미한다. 이렇게 되면 다른 Page로 이동할 수가 없기 때문에 그 Group 내에 빠지게 된다.
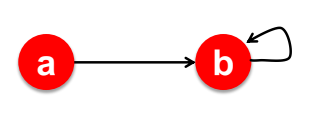
위 구조를 Spider Trap이라 부른다. 이 경우 처음에는 $r_a, r_b$가 [1, 0] 의 값을 가지지만, 1번 반복하는 경우 node b에서 빠져나올 수 없어 $r_a, r_b$는 [0, 1]의 고정된 값을 가지게 된다. 이렇게 되면 node의 중요도는 무시된 채 node b가 가장 중요한 node로 판단되기 때문에 문제가 된다. 이 경우에는 self-loop로 매우 간단한 예제이지만, cycle 구조를 가진 경우에도 발생할 수 있다.
Solution
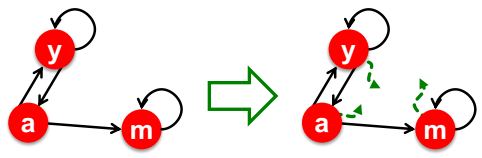
Spider Trap에서 빠져나오기 위해서 PageRank에서는 $\beta$를 도입하였다. $\beta$는 random sufer가 link를 따라 움직이는 것을 의미하고, $1-\beta$는 random page로 teleport하는 것을 의미한다. spider trap에 빠졌을 때 teleport를 통해 빠져나오는 것이다. 일반적으로 $\beta$는 0.8이나 0.9로 설정한다.
Google에서는 Spider Trap에서 빠져나오기 위해 $\beta$를 도입하였으며, 최종적으로 $r$을 다음과 같이 정의하였다. 논문
\[ r_j = \sum_{i \rightarrow j} \beta \frac{r_i}{d_i} + (1-\beta) \frac{1}{N} \]
위 수식은 Dead end에 대해서는 고려하지 않았다. 따라서, 기존에 Dead end를 제거하거나 Dead end에서 각 node로 빠져나올 수 있는 확률을 부여하는 형태로 수정을 해주어야 한다. 위 수식은 flow-based fomulation이기 때문에 matrix formulation으로 변형하면 아래와 같은 수식이 도출된다.
\[ G = \beta M + (1-\beta) \left[\frac{1}{N}\right]_{N \times N} \]
$[1/N]_{N \times N}$은 matrix의 속성이 모두 1/N인 것을 의미한다. 최종적으로 $r= G \cdot r$을 최적화하는 문제로 접근할 수 있다.
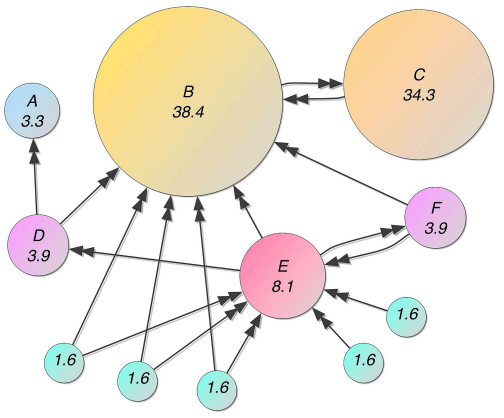
오른쪽 그림의 경우 node B의 중요도가 가장 높다. node E의 경우 in-link가 node B와 동일한 수를 가지고 있으나, in-link로 연결된 node들이 별로 중요하지 않은 node들이다. 따라서, 상대적으로 중요도가 높은 node와 in-link 관계를 가지고 있는 node B의 중요도가 node E에 비해 높은 것을 확인할 수 있다. 또한, node A의 경우 Dead ends이지만 중요도가 측정되는 것을 확인할 수 있다. node C의 경우 in-link가 node B에 대해서만 존재하지만 중요도는 높게 측정되었다.
Limitation
위에서는 DeepWalk, PageRank 등의 모델이 어떤 형태로 진행되는지에 대해서 다루었다. 이번 챕터에서는 해당 기법들이 가지는 한계점에 대해서 다루어보자.
recompute
기본적으로 현재 그래프의 구조 내에서 embedding을 진행하기 때문에 train set에서는 존재하지 않는 노드가 새롭게 유입되는 경우 이를 반영하는 것이 어렵다. 새로운 노드가 들어오게 된다면 다시 처음부터 학습을 진행해야 한다는 문제점이 존재하낟. 소셜 네트워크와 같은 도메인에서는 새로운 사용자의 유입이 많은데 이와 같은 도메인에서 이를 적용할 경우 엄청난 계산 비용이 요구된다.
structural similarity
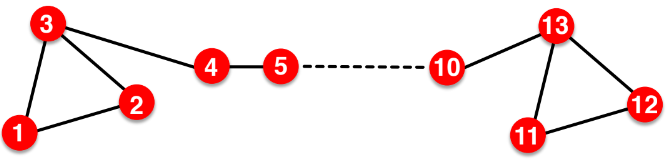
아래와 같은 구조를 가진 그래프는 구조적으로 유사하다. 노드 1은 노드 11과 유사하며 노드 2, 3은 각각 12,13과 유사하다. 그러나 random walk 방식을 사용하는 경우 이와 같은 그래프 구조에 대한 유사도를 포착하지 못한다. 만약 그래프 구조에 대해서도 학습하고 싶은 경우에는 anonymous walk를 사용하면 된다.
node feature
random walk의 학습 방식을 살펴보면 단순히 순서만 고려한다. 구체적으로, node feature와 같은 정보를 고려하지 않는다. 그렇기 때문에 노드의 표현을 제대로 학습하는 것에 한계가 존재할 수 있다.
'Deep Learning > CS224W' 카테고리의 다른 글
| [CS224W] Message Passing and Node Classification (3) | 2022.08.08 |
|---|---|
| [CS224W] Embedding Entire Graphs (0) | 2022.07.13 |
| [CS224W] Node Embeddings (0) | 2022.07.05 |
| [CS224W] Traditional feature-based methods: Graph-level features (0) | 2022.07.04 |
| [CS224W] Traditional feature-based methods: Link-level features (2) | 2022.07.03 |