Contents
이번 글은 CS224W의 Lecture 5.1 에 대한 내용을 다루고 있다. 해당 챕터에서는 Message Passing과 Node Classification에 대한 내용을 포함하고 있다. 일반적으로 Semi-Supervised Learning을 할 때 사용하며, 일부 노드의 label에 대한 정보가 주어졌을 때, 모든 노드에 label을 부여하는 방법에 대해서 다룬다.
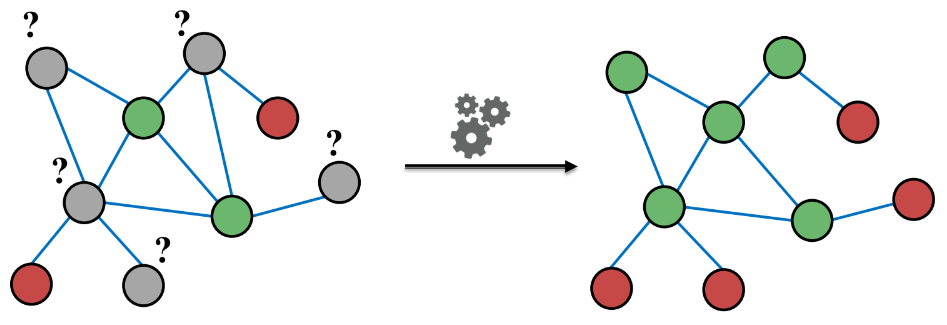
Massage Passing은 Node Classification을 하는 방법 중 하나이며, 그 중 Relational Classification, Iterative Classification, Belief Propagation에 대해서 알아보자.
Node Classification
Node Classification은 기본적으로 연결되어 있는 노드들은 서로 같은 label을 가지고 있을 것이라는 가정 하에 진행된다. 즉, 노드 간의 관계를 통해서 계산하게 된다. 그래프에서 관계를 계산하는 방식은 Homophily, Influence로 나뉜다. Homophily는 노드들의 개별적인 특성을 바탕으로 Social Connection를 보는 것이며, Influence는 반대로 Social Connection을 바탕으로 노드들의 개별적인 특성을 파악하는 것이다.
Homophily는 노드들이 유사한 다른 노드들과 연합(associate)하고 결속(Bond)하려는 경향을 의미한다. 사자성어로는 "유유상종"을 의미한다. 예를 들어, 같은 분야를 공부하고 있는 연구원들은 서로 Connection이 있을 가능성이 높다라는 것이다. Influence는 Homophily와는 반대로 Social Connection을 기반으로 Individual Characteristics을 확인하는 것이다. 사회적인 연결은 사람들의 개별적인 특성에 영향을 줄 수 있다는 가정에서 시작된다.
위에서 다룬 Homophily, Influence와 같은 Correlation을 가지고 어떻게 노드의 label을 예측하는 데 사용할 수 있을까? 아래의 그림에서 초록색은 Positive를 의미하고, 빨간색은 Negative를 의미한다. 이때 회색 노드의 라벨을 예측해보자.

초록색 노드와 연결된 회색 노드의 경우 초록색일 확률이 높고, 빨간색 노드와 연결된 회색 노드의 경우는 빨간색일 확률이 높을 것이다(Guilt-by-association). 위에서도 언급했듯 Semi-Supervised Learning을 할 때는 이와 같은 가정을 기반으로 진행하며, 그래프가 주어졌을 때 labeling이 되어 있지 않은 노드의 색을 찾는 것이 목표다.
Collective Classification
Collective Classification은 Local Classifier, Relational Classifier, Collective Inference 총 3가지 단계로 구성되어 있다. 이는 상관관계(Correlation)을 통해서 연결된 노드들을 분류하는 방식이며, Markov Assumption을 사용한다. Markov Assumpytion은 label $Y_v$은 node $v$의 이웃에 의존적이다는 것을 가정한다.
\[ P(Y_v) = P(Y_v|N_v), \quad (Y_v = \{0, 1\}) \]
$Y_v$는 label을 나타내는 변수를 의미한다. $N_v$는 node $v$와 연결된 이웃을 의미한다.
Local Classifier
Local Classifier는 초기 label을 할당하는 단계다. node attributes/feature를 기반으로 label을 예측하며, 일반적인 classification task를 의미한다. 그러나, 이는 network information은 사용하지 않는다. 그렇기 때문에 Local Classifier는 회색 노드에 초기 label을 지정하기 위해서 초기에 한 번만 적용된다.
Relational Classifier
Relational Classifier는 node $v$의 Class Probability $Y_v$는 이웃 노드의 class probabilities의 weight average라는 것을 기본 가정으로 설정한다. 이때 node $v$는 라벨링된 노드를 의미하고, $Y_v$는 초기 label을 의미한다. 이때, $Y^*_v$는 실제 label, 즉, ground-truth label을 의미한다. 라벨링이 되지 않은 노드의 초기 $Y_v$는 0.5로 설정한다. 이때 값이 수렴하거나 최대 반복 횟수에 도달할 때까지 임의의 순서대로 모든 노드를 업데이트 한다.
Collective inference
Collective inference는 상관관계를 전달하는 단계다. 반복적으로 적용하며, 이웃 노드 label 간의 Loss가 최소화될 때 까지 반복한다.
위에서는 Collective Classification이 어떻게 구성되어 있는지, 각 단계가 어떤 역할을 하는지에 대해서 알아보았다. 그렇다면 Collective Classification이 실제로 어떻게 문제를 해결하는지에 대해서 알아보자.

우리의 목적은 위 그림에서 회색 노드의 라벨을 분류하는 것이다. 이때 node $v$의 feature vector는 $f_v$로 정의한다. 초록색 node의 경우 1로 정의하고, 빨간색 node의 경우는 0으로 정의한다. 이때 모든 node의 feature가 주어졌을 때 $P(Y_v)$를 찾는 것이 바로 목적이다.
위 연구는 Homophily를 기반으로 진행하고 있으며, 이는 유사한 노드의 경우 인접해 있다고 가정한다. 본 챕터에서는 이러한 가정으로 진행하는 Relational Classification, Iterative Classification, Belief Propagation 총 3가지 모델을 소개한다.
Relational Classifier
Relational Classifier는 node $v$의 Class에 대한 확률 $Y_v$는 각 이웃의 Class에 대한 확률의 weighted average라는 것을 가정하고 있다. 즉, 주변 node의 Class에 대한 정보를 바탕으로 노드 $v$의 Class를 찾는다는 것이다. 라벨링된 node $v$는 초기 $Y_v$를 ground-truth로 지정하고, 라벨링되지 않은 node의 $Y_v$는 0.로 지정한다. 이 과정을 값이 모든 노드의 값이 수렴하거나 iteration이 끝날 때 까지 반복하면서 업데이트하며, 각 노드에 대한 업데이트 수식은 다음과 같다.
\[ P(Y_v = c) = \frac{1}{\sum_{(v,u) \in E} A_{v,u}} \sum_{(v,u) \in E } A_{v,u} P(Y_u = c) \]
edge의 strength 혹은 weight가 존재하는 경우 $A_{v,u}$는 node $v$, $u$ 간의 edge weight를 의미한다. $P(Y_v = c)$는 node $v$가 라벨 C일 확률을 의미한다. 이때의 Challenges는 위 수식이 수렴하지 않을 수 있으며, Model이 node feature 정보를 사용할 수 없다는 것이다.
Example

위 그림은 Relational Classifier의 학습 과정을 나타낸다. 라벨링된 node는 초록색인 경우 1로, 빨간색인 경우 0으로 할당되고, 라벨링 되지 않은 회색 node는 0.5로 초기값을 할당한다.

node 3을 확인하면 node 3의 주변 node는 빨간색 node 두 개와 회색 node 하나로 구성되어 있다. 빨간색 node의 경우 0의 값을 가지고 있으며 회색 node의 경우 0.5의 값을 가지고 있다. 이를 average하면 0.17이 도출된다.

node 3을 업데이트하고 난 후 node 4를 업데이트 한다. node 4의 경우 이웃 node로 node1, 3, 5, 6를 가지고 있다. 각각 node의 probability $Y$를 기반으로 average 하면 0.42라는 값이 도출된다.

node 3과 node 4를 업데이트 한 후 node 5를 업데이트 하는 과정이다 .위 방식과 동일하게 진행하면 0.73의 값이 할당된다.

나머지 node 9와 node 8에도 동일한 방식을 수행하면 node 9는 $P(Y_9) = 1, \\ P(Y_8) = 0.91$의 값을 도출한다.
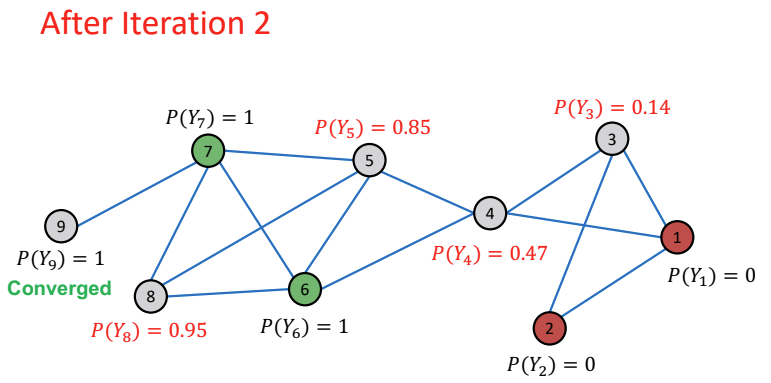
위 전체 과정을 한 번 더 반복하게 되면 node 3, 4, 5, 8의 값은 업데이트 되고, node 9의 값은 Converge하게 된다.


총 4번 수행한 결과 node 4를 제외한 나머지 node는 전부 수렴했다.

총 5번을 수행한 결과 모든 node의 값이 수렴하였으며, 이 때의 값을 기준으로 $P(Y_v)$의 값이 0.5보다 큰 경우 라벨을 1로 예측하고, 0.5보다 작은 경우 라벨을 0으로 예측한다.
Iterative Classification
Relational Classifier는 node의 속성하지 않았다. 단순히 node의 라벨을 가지고 라벨링 되지 않은 node의 라벨을 예측하는 semi-supervised learning을 진행하였다. iterative classification의 메인 아이디어는 이웃 node의 label $z_v$ 뿐만 아니라 node의 속성 $f_v$까지 고려한다는 것이다.
그래프가 주어졌을 때 node $v$의 feature vector는 $f_v$로 정의하고, node $v$의 라벨링된 값은 $Y_v$로 표기한다. 이때 라벨링 되지 않은 node를 예측하는 것을 목적으로 설정한다. Iterative Classification는 이웃 node의 label과 attribute를 사용하기 때문에 총 두가지 classifier가 존재한다. 첫 번째 classifier는 $\phi_1(f_v)$는 node feature vector $f_v$를 기반으로 node의 라벨을 예측하는 classifier이며, 두 번째 classifier는 $\phi_2(f_v, z_v)$는 node feature vector $f_v$와 이웃 node $v$들의 라벨의 합계 $z_v$를 기반으로 node의 라벨을 예측하는 classifier다.
그렇다면 이웃 node $v$들의 라벨의 합계 $z_v$를 어떻게 학습할까? 첫 번째로는 이웃 node의 라벨의 histogram을 생성해 이를 $z_v$로 사용하는 방법이 있다. 두 번째로는 이웃 node에서 가장 일반적인 label를 사용한다. 마지막으로는, 다른 node의 수를 사용한다.

Phase 1: Classify based on node attributes alone
Iterative Classification은 총 두 단계로 구성되어 있다. 먼저 첫 번째 단계에서 어떤 식으로 진행되는지 알아보자. 첫 번째 단계는 node의 attribute만 사용하여 분류하는 것이다. 해당 단계는 Classifier를 학습하는 단계이며, 이때 Classifier는 Linear classifier, Neural Network 등 다양한 모델을 사용할 수 있다.
Phase 2: Iterate till convergence
Iterative Classification의 두 번째 단계는 위 과정을 수렴할 때까지 반복하는 것이다. 테스트셋에서 $\phi_1$을 기반으로 label $Y_v$를 설정하고, $z_v$를 계산한 다음 $\phi_2$와 함께 label을 예측한다. 각 node $v$에서 반복하며 모든 이웃 node의 $Y_u$로 부터 $z_v$를 업데이트 하고, 새로운 $z_v(\phi_2)$를 통해 $Y_v$를 업데이트하는 것을 계속 반복한다. 이때 값이 안정화(stabilize)되거나 최대 반복 수에 도달할 때 까지 이를 계속한다. 그러나, Iterative Classification 역시 값이 수렴되지 않을 수 있다는 문제점이 존재한다.
Example
Iterative Classification은 Web Page Classification 예제를 통해 어떻게 작동하는지 알아보자. web page graph 데이터를 예로 들면, 이때 node는 web page가 된다. 그리고 edge는 web page 간의 hyper link가 된다. node feature는 webpage의 설명이 된다. 예제를 단순히 하기 위해 본 Lecture에서는 binary feature만을 고려했다. 이때는 webpage의 토픽을 예측하는 것을 목적으로 설정한다.

가운데 노드를 보면 아까 위에서는 파란색 즉, 라벨링 되지 않은 node였지만, 지금은 초록색으로 예측되었다. 실제 라벨은 0이기에 잘못 예측된 것이다.

이때 $I$는 이웃 node에서 들어온 information vector $z_v$를 의미하고, $O$는 나가는 이웃 라벨의 information vector $z_v$를 의미한다. 또한, $I_0$은 incoming page의 라벨이 0인 경우 1로 표기하고, $I_1$은 incoming page의 라벨이 1인 경우 1로 표기한다. 예를 들어, incoming page의 라벨이 0인 경우 [1, 0]으로 표기한다. 이때 Iterative Classifier는 어떻게 진행되는지를 알아보자.

첫 번째 단계는 classifier를 학습하는 단계다. Iteration Classifier는 $\phi_1$과 $\phi_2$로 구성되어 있으며, $\phi_1$은 node feature $f_v$만을 사용한다. 반면에, $\phi_2$는 node feature 뿐만 아니라 $z_v$까지 사용한다. 위 그림을 살펴보면 초록색 부분이 $\phi_1$가 사용하는 정보를 의미하고, 빨간색 부분이 $\phi_2$가 사용하는 정보를 의미한다.

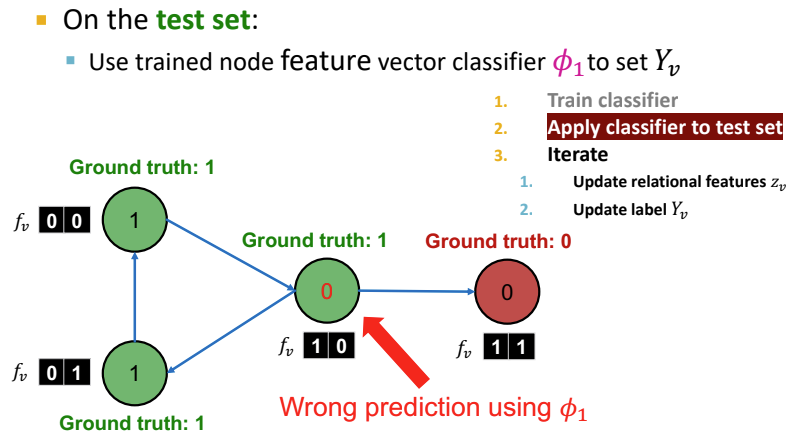
두 번째 단계에서는 학습된 Classifier $\phi_1$를 하여 $Y_v$를 설정한다. 위 과정에서는 Classifier가 제대로 학습되지 않아서 node의 라벨을 0으로 잘못 예측한 것이다.


세 번째 단계에서는 feature $z_v$를 업데이트 한다. 그 후 $\phi_2$를 사용하여 node를 다시 분류한다. $z_v$와 $Y_v = \phi_2(f_v,z_v)$를 업데이트 하면서 값이 수렴할 때 까지 계속 반복 작업을 수행한다. 위 그림의 $I$와 $O$를 살펴보면 outcoming과 incoming이 잘못 표기 되어 있다. 왜냐하면 처음에는 가운데 node의 라벨을 0으로 예측했기 때문이다. 그래서 incoming과 outcoming을 아래와 같이 교체하면서 최종적으로 예측을 수행하고 더이상 node feature의 변화가 없을 때까지 혹은 iteration 횟수가 끝날 때까지 반복한다.


Relational Classification은 주위 node의 라벨을 가지고 라벨링 되지 않은 node를 예측하는 형태로 값이 수렴하거나 iteration 횟수가 끝날 때까지 반복한다. 그러나 해당 방법은 node feature를 사용하지 않는다는 것이 단점이다. 이를 극복하기 위해 Iterative Classfication이 제안되었으며, Iterative Classification은 두 가지의 Classifier를 사용해 node feature와 이웃 node의 라벨까지 사용한다. Relational Classification과 Iterative Classification은 결정적으로 둘다 수렴하지 못할 수도 있다는 문제점이 존재한다. 그렇다면 Collective Classification 중 마지막인 Belief propagation을 알아보자.
Loopy Belief Propagation
Belief Propagation은 그래프의 probability queries에 응답하는 동적 프로그래밍을 의미한다. 이웃 노드들이 "talk"하여 서로 메세지를 주고받는 반복적인 프로세스를 의미한다. 메세지는 주변 node 간의 주고 받는 정보 정도로 이해하면 된다. 이때 각각의 node들이 전달하는 메세지들이 일치하면 최종 belief를 계산한다.

그래프 안에 존재하는 노드의 수를
'Deep Learning > CS224W' 카테고리의 다른 글
| [CS224W] PageRank (0) | 2022.07.18 |
|---|---|
| [CS224W] Embedding Entire Graphs (0) | 2022.07.13 |
| [CS224W] Node Embeddings (0) | 2022.07.05 |
| [CS224W] Traditional feature-based methods: Graph-level features (0) | 2022.07.04 |
| [CS224W] Traditional feature-based methods: Link-level features (2) | 2022.07.03 |