[CS224W] Embedding Entire Graphs

Contents

• Embedding Entrie Graphs
  • Approach 1
  • Approach 2
  • Approach 3: Anonymous Walk

 

Embedding Entrie Graphs

Approach 1

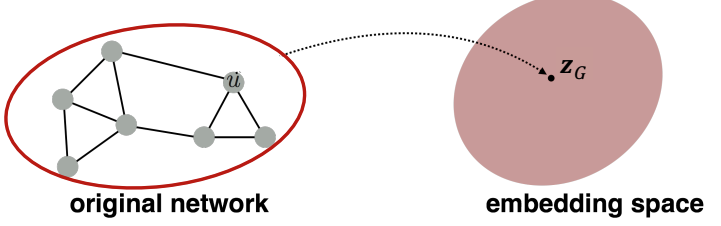
본 강의에서는 node embedding이 아닌 entire graph를 embedding 하는 방법에 대해서 다룬다. graph embedding은 subgraph나 전체 entire graph를  embedding하는 것이 목표라고 할 수 있다.

이때 $z_G$는 graph embedding을 의미하며, toxic molecules와 non-toxic molecule를 구분하거나, 비정상적인 graph를 식별하는 것에 활용할 수 있다. 가장 간단한 아이디어는 graph에 속한 node embedding을 합하거나 평균을 취하는 것으로도 가능하다. 

$$z_G=\sum _{v\in G}{z}_v$$

 

Approach 2

다음으로는 ''virtual node''를 만들어서 embedding하는 것이다. 아래의 그림과 같이 subgraph에서 node 들에 virtual node를 생성한 후 이를 embedding space로 encoding해서 사용하는 방법이며, Li et al., (2016)이 처음으로 제안하였다. 

 

Approach 3: Anonymous Walk

entire graph를 embedding하는 경우에도 Random Walk와 비슷한 방법의 Anonymous Walk (ICML, 2018)를 사용한다. Random Walk의 경우는 start node에 따라 다양한 index가 도출될 수 있지만, Anonymous Walk는 단순히 node의 패턴만을 고려하는 것이다. 

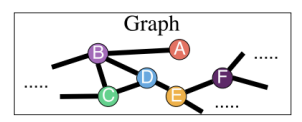
예를 들어 Random Walk 1은 $A\to B\to C\to B\to C$라고 한다면 1, 2, 3, 2, 3으로 표현할 수 있다. Random Walk 2의 경우에도 $C\to D\to B\to D\to B$로 움직이기 때문에 단순히 node의 움직임만 본다면 1, 2, 3, 2, 3으로 Random Walk 1과 동일한 패턴이 도출된다. 즉, 동일한 sequence를 가진 경우 이를 같은 Walk로 보는 것이다. 이와 같은 방식으로 값을 계산하는 것이 바로 Anonymous Walk다. 

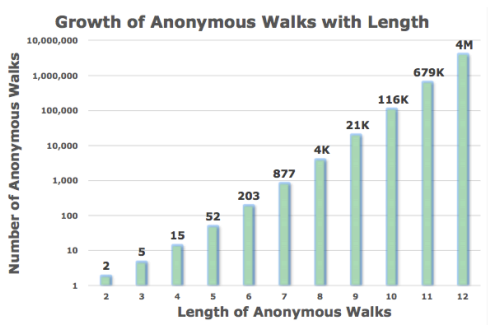
위 그림은 Walk의 길이에 따른 Anonymous의 개수를 의미한다. 예를 들어, Walk의 길이가 3인 경우, $w_1$=111, $w_2$=112, $w_3$=121, $w_4$=122, $w_5$=123 으로 총 5개가 존재한다. Walk의 길이가 2인 경우에는 $w_1$=11, $w_2$=12 만 존재하기 때문에 2개의 Anonymous Walk가 존재한다. 

 

우리는 graph embedding을 최적화 하기 위해 $l$-step 만큼 anonymous walks를 반복하고 이를 기록한다.  예를 들어, $l$=3인 경우, 가질 수 있는 총 Anonymous의 개수는 5개이기 때문에 5차원의 벡터 공간 내에 발생 빈도를 측정하는 것이다. 만약 111, 121, 123이 발생한 경우 $z_G$=[1, 0, 1, 0, 1]로 기록하는 것이다. 이때의 오차를 바탕으로 graph embedding을 수행하며, 우리가 원하는 오차 범위 내로 Graph embedding을 수행하기 위해서는 m 번 만큼 반복해야 된다. 

$$m=[\frac{2}{{ϵ}^2}(\log (2^{\eta }-2)-\log (\delta ))]$$

$\eta$는 Anonymous Walks의 개수를 의미하고, $ϵ$과 $\delta$는 오차를 의미한다. random walk를 m 번 반복할 경우 $ϵ$와 $\delta$ 사이의 오차를 가진 분포가 도출된다. $ϵ=0.1,\delta =0.01$ 사이의 오차를 원하는 경우, $l$=7을 기준으로, 총 122,500 번의 random walk를 수행하여야 한다.

 

Learn Walk Embeddings

딥러닝에서는 단순히 빈도의 형태로 Embedding을 하는 것이 아니라 Embedding을 학습하는 방식으로 진행된다. 그렇다면 당연히 Graph Embedding도 학습을 하는 방식이 존재할 것이다. Graph Embedding에서는 다음 번의 walk를 예측하는 형태로 학습할 수 있다. 

 

graph vector $z_G$가 주어졌을 때 $\mathrm{\Delta }$-size window의 동시 발생 빈도를 예측하면서 학습하는 것이다. 예를 들어 window size가 1인 경우($\mathrm{\Delta }=1$) $w_1,w_3$이 주어지고 $w_2$를 예측하는 것을 의미한다. 이와 같은 방식은 DeepWalk와 node2vec과 매우 유사한 방식을 띄며, 수식으로 표현하면 다음과 같다. 

$$max\sum _{t=\mathrm{\Delta }}^{T-\mathrm{\Delta }}\log P(w_t|w_{t-\mathrm{\Delta }},...,w_{t+\mathrm{\Delta }},z_G)$$

위 과정을 총 T 번 반복하게 된다면 starting node $u$에 대해서 다음과 같은 random walk 집합을 만든 후 목적 함수로 최적화할 수 있다. 

$$N_R(u)=\{w_1^u,w_2^u,...,w_T^u\}$$

$$\underset{Z,d}{max}\frac{1}{T}\sum _{t=\mathrm{\Delta }}^{T-\mathrm{\Delta }}\log P(w_t|\{w_{t-\mathrm{\Delta }},...,w_{t+\mathrm{\Delta }},z_G\})$$

$$P(w_t|\{w_{t-\mathrm{\Delta }},...,w_{t+\mathrm{\Delta }},z_G\})=\frac{\exp (y(w_t))}{\sum _{i=1}^{\eta }\exp (y(w_i))}$$

$$y(w_t)=b+U\cdot (\text{cat}(\frac{1}{2\mathrm{\Delta }}\sum _{i=-\mathrm{\Delta }}^{\mathrm{\Delta }}{z}_i,z_G))$$

$\text{cat}(\frac{1}{2\mathrm{\Delta }}\sum _{i=-\mathrm{\Delta }}^{\mathrm{\Delta }}{z}_i,z_G)$는 window size 만큼의 anonymous walk embedding을 평균을 낸 후 graph embedding $z_G$와 결합(Concatetaed)한 것을 의미한다. 

이처럼 T 번의 Anonymous walk를 수행하고, 이를 Average 한 후 원래의 graph embedding과 결합하여 t의 anonymous walk를 예측하는 형태가 된다. (그림으로 보면 더 쉽다..) 상세한 구조가 궁금한 경우에는 Anonymous walk를 제안한 (ICML, 2018)을 찾아보자.

 

이렇게 해서 도출된 $z_G$를 통해서 Graph Classification에 사용할 수 있다. Graph Classification 뿐만 아니라 Node Classification, Link Prediction, Clustering/community detection 등 다양한 Task에 활용이 가능하다.