추천시스템은 우리가 가장 많이 접해볼 수 있다. 넷플릭스, 당근 마켓, 쿠팡, 카카오 등 여러 기업에서 사용한다. 넷플릭스의 경우는 사람간의 유사도를 평가해 해당 영화를 시청했을 때 그 영화와 줄거리가 비슷한 영화를 추천해주고, 카카오의 경우 카카오에서 어떠한 기사를 보면 그 기사의 토픽을 보고 비슷한 기사를 추천해주는 방법을 사용하고 있다. 이렇게 추천시스템은 우리의 일상에 이미 동화되어 있다.
롱테일의 법칙
롱테일의 법칙은 하위 80%가 상위 20%의 가치보다 크다는 법칙이다. 추천시스템을 이야기 하는데 왜 갑자기 롱테일의 법칙을 이야기 할까? 다소 동 떨어진 의미라고 생각할 수 있지만 현재 추천시스템을 사용하는 기업들은 상위 20% 의 고객에 초점을 맞추기 보다는 하위 80% 의 고객에게 초점을 맞추어 상품을 추천하고 제품을 구성한다. 이런 추천방법은 아무래도 오프라인보다는 온라인에 조금 더 취중된 시스템이라고 볼 수 있다.
온라인에서는 롱테일의 법칙을 어떻게 사용할까?
유튜브나 넷플릭스를 예로 들 수 있을 것이다. 넷플릭스에서 영화를 볼때는 본인이 관심가지는 영화를 위주로 추천을 받게 된다. 즉, 가장 많이 시청하는 영화나 드라마가 아닌, 고객에 맞춤 서비스를 제공해주는 것이다. 유튜브도 알고리즘을 보면 고객들 개개인이 좋아하는 영상을 추천해준다. 만약 유튜브에서 개개인의 추천 알고리즘을 통한 영상 제공이 아닌 단순히 사람들이 많이 보는, 인기에 준거하여 영화를 추천해주었다면 지금처럼 성장할 수 있었을까?

추천시스템에는 여러가지 종류가 있다. 2005~2010년도 Apriori algorithm을 시작으로 2010~2015년에는 협업 필터링(CF), 2013~2017년에는 Spark를 이용한 빅데이터 FP-Growth, Matrix Factorization, 2015~2017년에는 딥러닝을 활용하여 협업 필터링과 딥러닝을 접목시키는 Item2Vec, Doc2Vec 등이 나오고 2017년 이후부터 현재까지는 딥러닝과 강화학습 등 여러가지 기법을 접목시켜 추천시스템을 만들고 있다.
Association Analysis
연관분석은 룰기반으로 상품과 상품사이에 어떤 연관성이 있는지 찾아내는 알고리즘이다. A라는 상품을 구매할 때 B라는 상품을 얼마나 많이 구매하게 되는가? 하는 것과 A라는 상품을 구매하는 사람이 B라는 상품도 구매하는가? 라는 규칙을 찾아내는 형태이다. 어떤 상품들이 한 장바구니 안에 담기는 지 살피는 모습과 비슷하기 때문에 장바구니 분석이라고도 표현하기도 한다. 연관분석에서 활용되는 metric은 다음과 같다.
Support ( 지지도 )
지지도는 상품 A와 B를 같이 구매할 확률이다. 즉, $P(A \cap B)$라고 한다. 일부 책에서는 $A \rightarrow B$라고도 표현한다. 전체 상품들 중에서 상품 A와 B를 같이 구매할 확률이다. $P(A \cap B)$가 클수록 같이 구매하는 비율이 높다고 생각할 수 있다. 하지만 단순히 그렇게 생각하면 오류가 발생한다. 예를 들어 매일 구매하는 생필품을 상품 B라고 하고 노트북을 상품 A라고 하자. 생필품은 비교적 매일 구매가 이루어질 것이다. 당연히 이마트에서 노트북을 구매하면서 생필품(휴지, 치약, 칫솔 등)을 구매했을 수도 있다. 이 경우 두 관계를 어떻게 판단해야할 까? 이런 문제점들 때문에 상품을 대분류 혹은 중분류, 소분류로 나누어 확률값을 도출해야될 경우도 생긴다.
아래의 표를 보고 상품 A를 맥주로 하고, 맥주를 구매할 때 다른 상품들이 어떤 지지도를 가지는지 구해보자.
전체 장바구니의 수 : 5, 맥주(A), 다른 상품(B)
$P(A \cap B)$가 40%인 상품 : 오징어
$P(A \cap B)$가 20%인 상품 : 치즈, 사이다, 콜라, 라면, 소주
confidence ( 신뢰도 )
신뢰도는 상품 A를 구매했을 때 상품 B를 구매할 확률 $ P(B|A) = { P(A \cap B) \over P(A) } $ 로 우리가 일반적으로 알고 있는 조건부 확률이다. 위 에서 본 지지도를 $P(A)$ 로 나누어준 값으로 볼 수 있으며, 상품 A를 구매한 확률을 전체 확률로 보고 그 안에서 상품 B도 같이 구매한 확률을 말한다. 신뢰도도 다음과 같이 구할 수 있다.
전체 장바구니의 수 : 5, 장바구니 내 맥주 출현 횟수 : 3
${P(A \cap B) \over P(A)}$ = ${ 2 \over 3 } $ : 66% 인 상품 : 오징어
${P(A \cap B) \over P(A)}$ = ${ 1 \over 3 } $ : 33% 인 상품 : 치즈, 사이다, 콜라, 라면, 소주
lift ( 향상도 )
향상도는 상품 A와 상품 B의 사건이 얼마나 동시에 발생하는지 독립성을 측정하게 된다. 향상도에 대한 식을 살펴보면 $P(A \cap B) \over P(A)P(B)$로써 분모에는 $P(A)$와 $P(B)$가 독립일 때의 확률 값을 두었고, 독립인 기준으로 $P(A \cap B)$ 에 대해서 측정했다. 향상도를 알아보기 위해 A상품은 맥주, B상품은 콜라, C상품은 라면이라고 하면 수식은 다음과 같다.
$P(A)$ = ${3 \over 5},$ $P(B) = { 1 \over 5} ,$ $P(C) = { 3 \over 5 } ,$ $P(A \cap B) = {1 \over 5},\ \ P(A \cap C) = {1 \over 5}$
$ { P(A \cap B) \over P(A)P(B)} $ = ${5 \over 3} \approx 1.67 $
$ { P(A \cap C) \over P(A)P(C)} $ = ${5 \over 9} \approx 0.56$
위 결과와 같이 맥주와 콜라 간의 향상도는 1.67로 근사하고, 맥주와 라면 간의 0.56에 근사한 것을 볼 수 있다. 지지도와 향상도의 범위는 $ 0 \le Probabiliy \le 1 $ 이지만 향상도의 범위는 지지도와 신뢰도와는 조금 다르다. 향상도는 1을 기준으로 1보다 작으면 둘 간의 관계가 낮다고 보고 1보다 크면 관계가 있다고 보며, 1인 경우에는 서로 독립이라고 본다.

향상도가 무엇일까?
일반적으로는 지지도와 신뢰도만 가지고 상품 간의 관계를 유추하게 되는데 다음과 문제에 직면하게 돼 향상도의 중요도가 대두되었다. 위 수식들을 통해서 맥주를 구매하는데 콜라와 라면에 대한 신뢰도가 동일한 것을 확인할 수 있었다.. 맥주와 콜라에 대한 신뢰도와 맥주와 라면에 대한 신뢰도가 둘다 33% 라고 하면 맥주가 3번 구매가 이루어졌을 때 콜라와 라면에 대한 구매는 1번이 이루어 졌다고 할 수 있다. 전체 구매리스트에서는 콜라는 1번, 라면은 3번 등장했다. 이 경우에는 콜라와 맥주 중에 어떤 상품을 추천해주는 것이 고객에게 더 큰 만족도를 제공해줄 수 있을까?
구매 목록을 보면 라면은 일반적으로 사람들이 선호하는, 즉, 인기있는 상품이라고 볼 수 있다. 하지만 콜라의 경우에는 맥주를 구매할 때에만 구매가 이루어졌다. 이 경우에는 고객에게 인기있는 상품인 라면을 추천해주는 것이 아니라 맥주를 살 때 같이 구매를 하게되는 콜라를 추천해주는 것이 고객에게 더 큰 만족도를 제공해줄 수 있을 것이다. 조금 더 깊게 들어가자면 위 상품들로 구매할 수 있는 모든 가짓 수를 구해서 최고의 만족도를 끌어낼 수 있는 상품을 추천해주는 시스템을 개발하는 것이다.
문제점
연관분석의 경우 상품의 수가 많아질 수록 기하급수적으로 구해야되는 규칙의 수가 증가하게 된다. 이러한 문제점 때문에 요즘에는 잘 사용하고 있진 않다. 연관 분석의 문제점을 보완하기 위해 Apriori 알고리즘이 출현했다.

Apriori 알고리즘
a prior 원리는 아이템셋의 증가를 줄이기 위한 방법론이다. 기본적인 아이디어는 '자주 구매하는 아이템셋은 하위 아이템셋 또한 빈번할 것이다'라는 생각으로 출발했다. '해당 아이템 셋이 빈번하게 구매되지 않는다면 아래 하위 아이템 셋 역시 구매율이 낮을 것'이라 생각하여 하위 아이템 셋을 지워버린다.
1. k개의 item을 가지고 단일항목집단을 생성
2. 단일항목집단에서 최소 지지도 이상의 항목만 선택
3. 2에서 선택된 항목만을 대상으로 2개 항목집단을 생성
4. 2개 항목집단에서 최소 지지도 혹은 신뢰도 이상의 항목만 선택
5. 위 과정을 k개의 k-item frequnet set을 생성할 때 까지 반복

a priori 를 말로 설명하기 보다는 아래 코드와 수식으로 확인해보자.
imp = [
['맥주','오징어','치즈'],
['소주','맥주','라면'],
['맥주','오징어','사이다','콜라'],
['사이다','오징어','라면'],
['치즈','라면','계란']
]
te = TransactionEncoder().fit(imp)
te_ary = te.transform(imp)
print(te_ary)
# [[False False True False False True True False]
# [False True True False True False False False]
# [False False True True False True False True]
# [False True False True False True False False]
# [ True True False False False False True False]]
implicit = pd.DataFrame(te_ary, columns = te.columns_ ,index = ['홍길동','고길동','이순신','강감찬','정약용'])
implicit
# 계란 라면 맥주 사이다 소주 오징어 치즈 콜라
# 홍길동 False False True False False True True False
# 고길동 False True True False True False False False
# 이순신 False False True True False True False True
# 강감찬 False True False True False True False False
# 정약용 True True False False False False True False
freq_items = apriori(implicit, min_support = 0.2, use_colnames = True)
freq_items.index
# >>> freq_items.index
# RangeIndex(start=0, stop=33, step=1)
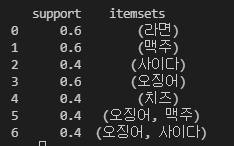
freq_items = apriori(implicit, min_support = 0.4, use_colnames = True)
freq_items.index
# >>> freq_items.index
# RangeIndex(start=0, stop=7, step=1)위 코드를 실행하면 아래와 같은 결과값이 출력된다. 최소 지지도를 0.2로 하면 아래처럼 총 33개의 itemset이 존재하지만 최소 지지도를 0.4로 조정하게 되면 7개의 itemset으로 추려진다. 더 많은 데이터를 써봐야 정확한 시간 차이를 알 수 있겠지만 확실히 경우의 수가 많이 줄었기 때문에 속도가 빠른 것을 짐작할 수 있다.
연관 분석에 비해 Apriori 알고리즘의 속도가 많이 향상되었다고는 하지만 아직 연산량이 많아 계산의 복잡도가 크게 된다. 그래서 속도를 빨리 하기 위해 FP-Growth 알고리즘이 등장했다.
FP-Growth 알고리즘
FP-Growth 알고리즘은 Apriori 알고리즘의 속도를 개선하기 위해 트리 구조의 형태로 아이템 셋을 구성했다. 기본 시작 구조는 위 방법들과 동일하다.
1. 모든 거래를 확인하여, 각 아이템마다의 지지도를 계산하고 최소 지지도이상의 아이템만 선택
2. 모든 거래에서 빈도가 높은 아이템 순서대로 순서를 정렬
3. 부모 노드를 중심으로 거래를 자식노드로 추가해주면서 tree를 생성
4. 새로운 아이템이 나올 경우에는 부모노드부터 시작하고, 그렇지 않으면 기존의 노드에서 확장
5. 위의 과정을 모든 거래에 대해 반복하여 FP TREE를 만들고 최소 지지도 이상의 패턴만을 추출
위 방법론들과 다른 점은 기존에 있던 노드에 이어 붙히는 형식이기 때문에 똑같은 값을 두 세번 적지 않아도 되는 장점이 있다. 하지만 앞 알고리즘에 비해 설계하기가 어렵다. 이 방법 역시 대용량으로 갈수록 속도의 한계에 직면하게 된다.

'Deep Learning > Recommender system' 카테고리의 다른 글
| [Recommender System] Collaborative Filtering, Content-based, Knowledge-based (0) | 2022.01.03 |
|---|---|
| [Recommender System] Metrics (0) | 2021.08.18 |
| [Recommender System] Neighborhood based method(CF) (0) | 2021.08.18 |
| [Recommender System] TF-IDF (4) | 2021.07.27 |
| [Recommender System] Emplicit data와 Implicit data란? (0) | 2021.07.14 |