[Recommender System] TF-IDF

TF-IDF 라는 개념에 들어가기 앞서 우리가 알아야할 개념들을 먼저 짚고 넘어가자. 점점 기술이 발전해가면서 텍스트에 대한 중요도가 높아지고 있다. 블로그, 의료 기록, 민원 등 다양한 곳에서 우리는 텍스트를 접해볼 수 있다. 우리는 이런 텍스트들을 비즈니스에 활용하기 위해 노력하는 단계이다. 

 

흔히 텍스트를 '비구조' 데이터라고 한다. 일반적인 데이터가 갖추어야 할 구조를 가지고 있지 않음을 뜻하며 텍스트 데이터는 각 데이터마다 길이도, 구조도 다르다. 맞춤법을 틀리는 경우도 있을 것이고, 단어를 섞고 축약하는 경우도 발생할 수 있다. 그리고 동일한 단어라고 하더라도 사용하는 분야에 따라 그 의미가 전혀 다른 경우가 발생할 수 도 있다. 또, 문맥을 파악하지 않으면 해당 단어가 어떤 뜻인지 파악하기가 어렵다. 

 

문서는 토큰$^{Token}$들의 집합으로 보는데, 가장 기본적인 유닛을 Token이라고 부르며, 문서를 모아놓은 것을 코퍼스$^{Corpus}$라고 부른다. 문서는 일반적으로 생각하는 문서의 경우도 해당하며, 유튜브 댓글이나 블로그 글 같은 경우도 모두 $Corpus$에 해당한다. 우리는 이러한 문서를 불러와 익숙한 특징 벡터 형태로 바꾸는 작업을 먼저 수행해야한다.

 

 

---

유사도

유사도를 구하는 방법은 엄청나게 많다.(Jaccard, Euclidean, Canberra, Ruzicka, ....) 우리는 다양한 유사도를 구하는 방법들 중 가장 많이 쓰이는 3가지 유사도에 대해서 알아보자. 

 

Euclidean

유클리디안 거리에 대해서는 다들 많이 들어봤을 것이다. 유클리디안 유사도는 유클리디안 거리에 대해 역수를 취해준 값이라 생각하면 된다. 유클리디안 거리는 계산하기가 쉽다는 장점이 있지만, 각 문서마다 분포가 다르거나 범위가 다른경우 상관성을 놓치기 때문에 normalization이 요구될 수도 있다. 

 

def uclidean_similarity(x, y):
    dis = np.sqrt(np.sum((x-y)**2))
    return 1 / (dis + 1e-5) 


doc1 = np.array((2, 3, 0, 1))
doc2 = np.array((1, 2, 3, 1))
doc3 = np.array((2, 1, 2, 2))
docQ = np.array((1, 1, 0, 1))


uclidean_similarity(doc1, docQ)
# 0.44721159550890216

uclidean_similarity(doc2, docQ)
# 0.31622676602000016

uclidean_similarity(doc3, docQ)
# 0.4082466238040005

 

 

 

Cosine

코사인 유사도는 각 단어에 대한 벡터값들을 가지고 두 벡터가 얼마나 유사한지를 판단하는 지표다. -1과 1사이의 값을 가지고, 1에 가까울수록 유사도가 높다는 것으로 해석할 수 있다. 텍스트 유사도를 구할 때 가장 널리 쓰이는 방법이며, 성능이 좋다고 한다. 하지만 벡터의 크기가 중요한 경우에 대해서는 잘 작동하지 않는다는 단점이 있다. 

 

 

$similarity = cos(\theta)  = {A\ \cdot\ B \over ||A|| ||B|| } = {\Sigma A_{i}B_{i} \over \sqrt{\Sigma A^2_i} \sqrt{\Sigma B^2_i}} $

# cosine similarity 

from sklearn.metrics.pairwise import cosine_similarity

print(cosine_similarity(df))
# [[1.         0.621059   0.66712438 0.9258201 ]
#  [0.621059   1.         0.85933785 0.59628479]
#  [0.66712438 0.85933785 1.         0.80064077]
#  [0.9258201  0.59628479 0.80064077 1.        ]]

 

 

Jaccard

자카드 유사도는 각 문서들을 하나의 집합으로 보고 그 집합 간에 얼마만큼 겹치는 부분이 있는지를 계산하는 방법이다. 자카드 유사도의 식은 다음과 같다. 

 

$J(A,B) = {|A \cap B| \over |A \cup B| } = {|A \cap B| \over |A| + |B| - |A \cap B| } $

 

def get_jaccard_sim(str1, str2): 
    a = set(str1.split()) 
    b = set(str2.split())
    c = a.intersection(b)
    return float(len(c)) / (len(a) + len(b) - len(c))

 

 

 

Bag of Word

Bag of Word는 중복을 허용하는 단어들의 집합이며, 집합 내에서는 문법, 단어 순서, 구둣점을 무시한다. BOW의 표현은 간단하면서 생성하는 데 연산이 적게 소요되며, 여러 종류의 작업에 잘 맞는다. 

 

 

단어의 빈도(TF)

 

우리는 BOW에 들어간 단어들을 가지고 단어$^{Token}$의 빈도를 확인할 수 있을 것이다. 단어의 빈도를 체크하기 위해서는 몇 가지 과정을 진행해야 한다.

 

1. 글자들을 정규화 하는 과정이 필요하다. 영어의 경우 대문자, 소문자로 되어 있는 단어들을 대문자로 혹은 소문자로 통일을 해주는 과정을 해준다.

 

2. 단어의 어근을 추출해 축약을 하거나, 복수형 단수형으로 축약해준다. 

 

3. Stopword 불용어를 제거해주어야 한다. 영어의 경우에는 the, a, of, on 같은 경우가 해당된다.

 

 

 

 

역문서 빈도(IDF)

빈도는 하나의 문서 안에서 어떤 단어가 얼마나 많이 나오는지를 측정하는 것이다. 그러나 단 어의 비중을 결정할 때에는 우리가 마이닝하는 전체 코퍼스 안에서 이 단어가 얼마나 흔하게 나오는지에 대해서도 신경을 써야 한다. 다음과 같이 두 가지의 상반된 측면에서 검토한다.

 

1. 단어가 너무 희박하면 안된다.

 

2. 너무 흔해도 안된다.

 

 

$IDF(t) = 1 + log({ 전체 문서 수 \over t가 나오는 문서 수}) $

 

 

 

TF-IDF

TF-IDF 는 TF와 IDF를 합친 지표이다. 

 

$TF-IDF(t, d) = TF(t, d) \times IDF(t) $

 

 

TF-IDF은 직관적인 해석이 가능하다는 장점이 있지만, 대규모 corpus를 사용할 경우에는 높은 차원을 가지며, 매우 sparse한 형태의 데이터를 가지고 있기 때문에 메모리상의 문제가 발생할 수 있다라는 단점을 가지고 있다. 

 

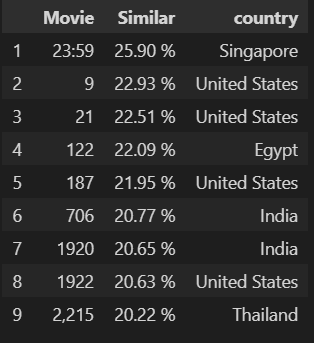
아래는 TF-IDF를 사용해서 영화 간 유사도를 측정하는 모델을 만든 코드이다.

import pandas as pd
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.metrics.pairwise import cosine_similarity


def Recsys(movie , rank = 10  , country = None , year = 1925, type = None):
    netf = pd.read_csv('netflix_titles.csv')

    feature_cols = ['title','type', 'country', 'release_year','listed_in', 'description']
    netf = netf[feature_cols]

    if type == 'Movie':
        netf = netf[netf['type'] == 'Movie']
    elif type == 'TV Show':
        netf = netf[netf['type'] == 'TV Show']



    # country
    if country != None:
        for i in range(len(country)):
            if i == 0 :
                net = netf[netf['country'] == country[i]]
            else:
                netflix = pd.concat([net, netf[netf['country'] == country[i]]])
    else:
        netflix = netf
    # starting year
    netflix = netflix[netflix['release_year'] >= year]

    word_vec = netflix['description']

    tfidf = TfidfVectorizer(min_df = 2, max_df = 0.7)

    tfidf_vec = tfidf.fit_transform(word_vec)

    # index = title, columns = word, value = word to vector 
    new_netflix = pd.DataFrame(tfidf_vec.toarray(), columns = tfidf.get_feature_names(), index = netflix['title'])

    # drop numeric columns
    string_col = [word for word in list(new_netflix.columns) if word.isalpha() == True]

    new_netflix = new_netflix[string_col]

    result = pd.DataFrame(cosine_similarity(new_netflix, new_netflix), columns = netflix['title'], index = netflix['title'])
    feature_col = list(result.columns)
    cty = netflix['country']
    score = [f'{x * 100 :0.2f} %' for x in result[movie].sort_values(ascending = False)]

    dic = pd.DataFrame(dict({'Movie' : feature_col, 'Similar' : score, 'country' : cty})).reset_index(drop=True)

    return dic.iloc[1:rank,:]

Recsys(movie = 'About Time', type = 'Movie', rank = 10)