K-Neighborhood based method(KNN)은 k개의 군집으로 clustering을 하는 머신러닝 기법 중 하나이다. 추천시스템에서 KNN이라 함은 Explicit Data 즉, 유저가 자신의 선호도를 직접 표현한 데이터를 가지고 새로 유입된 사용자 혹은 상품에 대해서 선호도를 예측하는 기법이라고 볼 수 있다.
User Based Collaborative Filtering
사용자 간 유사도를 측정해 사용자가 아이템에 해당하는 평점을 직접 입력하지 않더라도, 해당 사용자와 유사한 사용자의 평점을 가지고 사용자에 대한 아이템의 선호도를 예측하는 기법이다. 주로 코사인 유사도, 피어슨 유사도를 사용하여 유사도를 계산하여 측정한다. 주의해야할 점은 해당 사용자가 측정한 평점에 bias가 들어갈 수 있기 때문에 측정값에 평균을 빼주어 계산함으로써 bias를 해결할 수 있다.
Item Based Collaborative Filtering
User Based CB에서는 사용자 간의 유사도를 계산했지만 Item Based CB에서는 상품간 유사도를 계산하게 된다. 상품간 유사도를 계산해서 해당 상품을 구매했을 때 그 상품과 유사한 상품을 추천해주는 방법론이다.
장점
- 간단하고 직관적인 접근 방식 때문에 구현 및 디버그가 쉬움
- 특정 Item을 추천하는 이유를 정당화하기 쉽고 Item 기반 방법의 해석 가능성이 두드러짐
- 추천 리스트에 새로운 item과 user가 추가되어도 상대적으로 안정적
단점
- User 기반 방법의 시간, 속도, 메모리가 많이 필요
- 희소성 때문에 제한된 범위가 있음
- John의 Top-K 에만 관심이 있음
- John과 비슷한 이웃 중에서 아무도 해리포터를 평가하지 않으면, John의 해리포터에 대한 등급예측이 불가.
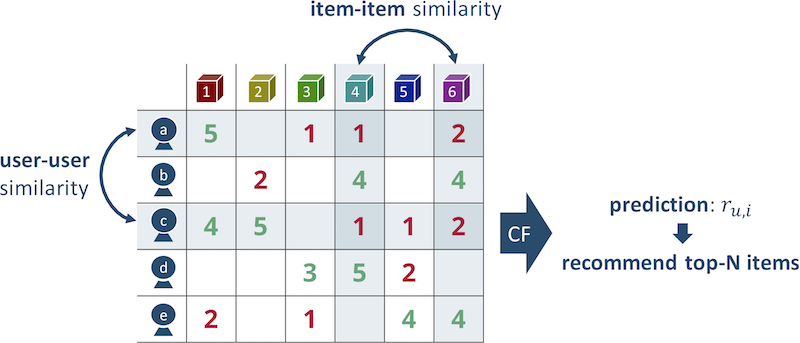
Keighborhood vs Latent Factor
이웃기반은 아이템에 대한 vector와 유저의 vector 간의 vector 유사도를 가지고 추천을 진행했다면, Latent Factor CB는 item기반의 latent space와 user기반의 latent space 두가지를 만들어 두 가지의 matrix에 대한 matrix 곱으로 추천을 진행하는 방식이다.
Latent Factor Collaborative Filtering
잠재 요인 CB는 Rating Matrix에서 빈 공간을 채우기 위해서 사용자와 상품을 잘 표현하는 차원(Latent Factor)을 찾는 방법이다. 잘 알려진 행렬 분해는 추천 시스템에서 사용되는 협업 필터링 알고리즘의 한 종류다. 행렬 분해 알고리즘은 사용자-아이템 상호 작용 행렬을 두 개의 저 차원 직사각 행렬의 곱으로 분해하여 작동하며 이 방법은 Netflix 챌린지에서 널리 알려지게 되었다. 해당 방법으로는 Observed Only MF, Weighted MF, SVD, SGD, ALS등이 있다.
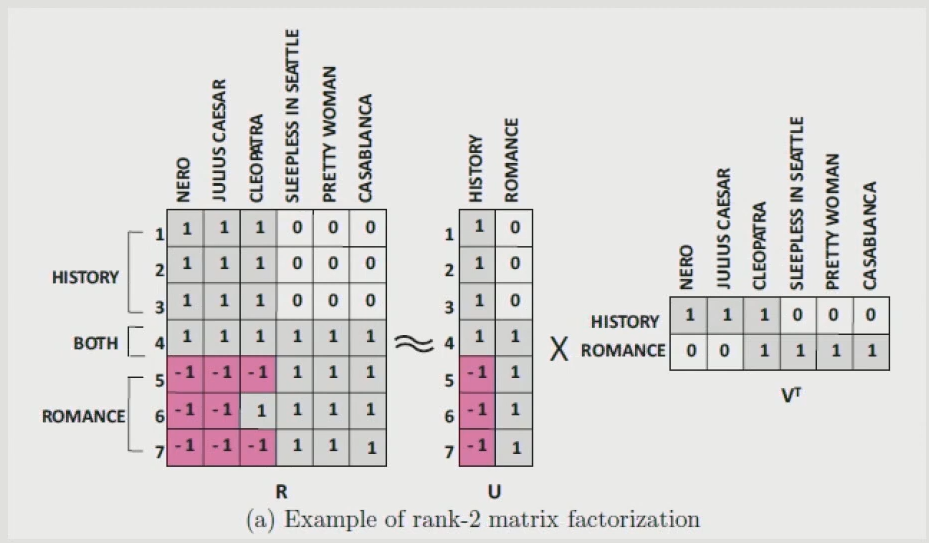
SGD
딥러닝에서 사용하는 방법으로 ${1 \over 2}||R-UV^{T}||^2$가 최소화 하려는 방법이다. 우리가 유저에 대한 행렬과 아이템에 대한 행렬을 뽑아냈는데, 그 행렬과 원래 행렬간의 차이를 줄이는 U와 V를 찾겠다는 것이다. 딥러닝이다보니 U와 V의 weight들이 계속 update되는데 역전파 알고리즘을 통해 weight값을 계속 update가 진행되는 방식이다. 딥러닝을 하다보면 weight를 update할 때 regularization term을 지정해두지 않으면 weight가 폭발적으로 변화하게 된다. 그 부분을 방지하기 위해 regularization term을 추가해주어야 한다.
$Minimize\ J ={1 \over 2}\underset{(i,j) \in S}{\Sigma}e^2_{ij} + {\lambda \over 2}\underset{i=1}{\overset{m}{\Sigma}} \underset{s=1}{\overset{k}{\Sigma}}u^2_{is} + {\lambda \over 2}\underset{j=1}{\overset{n}{\Sigma}} \underset{s=1}{\overset{k}{\Sigma}}v^2_{js}$
= $ {1 \over 2}\underset{(i,j) \in S}{\Sigma}(r_{ij} - \underset{s=1}{\overset{k}{\Sigma}}u_{is}\cdot v_{js} )^2 + {\lambda \over 2}\underset{i=1}{\overset{m}{\Sigma}} \underset{s=1}{\overset{k}{\Sigma}}u^2_{is} + {\lambda \over 2}\underset{j=1}{\overset{n}{\Sigma}} \underset{s=1}{\overset{k}{\Sigma}}v^2_{js}$
1. User Latent (U)와 Item Latent(V)를 임의로 설정.
2. 실제 값과 비교를 하면서 GD를 진행한다. ( 없는 값은 skip )
3. weight를 update한다. ( $ w - \eta * \partial U $ )
4. 2~3 과정을 반복 ( epoch 횟수만큼 )
장점
- 매우 유연한 모델로 다른 Loss function을 사용할 수 있음
- parallelized가 가능함
단점
- 수렴까지 속도가 매우 느림 ( 좋은 딥러닝 모델을 사용하면 해결가능 )
ALS
기존의 SGD가 두개의 행렬(U, V)을 동시에 최적화하는 방법이라면, ALS는 두 행렬 중 하나를 고정시키고 다른 하나의 행렬을 순차적으로 반복하면서 최적화하는 방법이다. 이렇게 하면, 기존의 최적화 문제가 convex 형태로 바뀌기에 수렴된 행렬을 찾을 수 있는 장점이 있다.
1. 초기 아이템, 사용자 행렬을 초기화
2. 아이템 행렬을 고정하고 사용자 행렬을 최적화
3. 사용자 행렬을 고정하고 아이템 행렬을 최적화
4. 2~3 과정을 반복.
평가를 하지 않아서 ? 로 들어간 value는 0으로 설정해서 진행한다.
Linear Regression를 할 때 $||y-X\beta||_2$에 대해서 $\beta$의 해를 구하는 것이 딥러닝에서는 $w$를 구하는 것이다. $\beta = (X^T X)^{-1} X^T y $로 나오며 SGD에서 사용한 Loss function 에 적용할 수 있다.
$\forall u_i : J(u_i ) = ||R_{i\cdot} - u_i \times V^T ||_{2} + \lambda \cdot\ ||u_i ||_2 $
$\forall u_j : J(u_j ) = ||R_{j\cdot} - U \times v^T_j ||_{2} + \lambda \cdot\ ||v_j ||_2 $
$u_i = (V^T \times V + \lambda \mathbf{I} )^{-1} \times V^T \times R_{i \cdot} $
$u_i = (V^T \times V + \lambda \mathbf{I} )^{-1} \times V^T \times R_{\cdot j} $
Collaborative Filtering
장점
- 도메인 지식이 필요하지 않음
- 사용자의 새로운 흥미를 발견하기 좋음
- 시작단계의 모델로 선택하기 좋음( 추가적인 문맥정보등의 필요가 없음 )
단점
- 새로운 아이템에 대해서 다루기가 힘듬
- side features( 고객의 개인정보, 아이템의 추가정보 )를 포함시키기 어려움
'Deep Learning > Recommender system' 카테고리의 다른 글
| [Recommender System] Collaborative Filtering, Content-based, Knowledge-based (0) | 2022.01.03 |
|---|---|
| [Recommender System] Metrics (0) | 2021.08.18 |
| [Recommender System] TF-IDF (4) | 2021.07.27 |
| [Recommender System] Association Rule (0) | 2021.07.23 |
| [Recommender System] Emplicit data와 Implicit data란? (0) | 2021.07.14 |